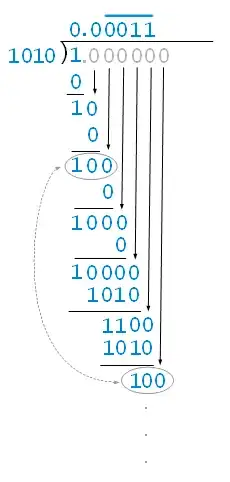
Tus programas sí pueden hacer cálculos aritméticos correctamente.
Por ejemplo, con el programa bc :
jose@luthien ~ $ bc
bc 1.06.95
Copyright 1991-1994, 1997, 1998, 2000, 2004, 2006 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
0.1+0.1
.2
0.1+0.2
.3
10*0.67
6.70
10*0.68
6.80
10*0.69
6.90
Con Java :
package testmatematicas;
import java.math.BigDecimal;
public class TestMatematicas {
public static void main(String[] args) {
BigDecimal ceroPuntoUno = new BigDecimal("0.1");
BigDecimal suma = ceroPuntoUno.add( ceroPuntoUno );
System.out.println( suma );
BigDecimal ceroPuntoDos = new BigDecimal("0.2");
suma = ceroPuntoUno.add(ceroPuntoDos);
System.out.println( suma );
BigDecimal diez = new BigDecimal("10");
BigDecimal ceroPuntoSesentaYSiete = new BigDecimal("0.67");
BigDecimal multiplicacion = diez.multiply(ceroPuntoSesentaYSiete);
System.out.println( multiplicacion );
BigDecimal ceroPuntoSesentaYOcho = new BigDecimal("0.68");
multiplicacion = diez.multiply(ceroPuntoSesentaYOcho);
System.out.println( multiplicacion );
BigDecimal ceroPuntoSesentaYNueve = new BigDecimal("0.69");
multiplicacion = diez.multiply(ceroPuntoSesentaYNueve);
System.out.println( multiplicacion );
}
}
La salida es :
0.2
0.3
6.70
6.80
6.90
Y, de hecho, en tu ejemplo el ordenador no está calculando incorrectamente la suma. Lo que está haciendo el ordenador es lo que hace siempre : Hacer lo que le has dicho, ESTRICTAMENTE, lo cual no tiene por qué ser lo que tu quieres que haga.
Cuando haces 0.1+0.2 parece que le pides que sume 0.1 a 0.2, cuyo resultado debiera ser 0.3
Pero no es así. Lo que en realidad le has dicho al ordenador que haga es :
Interpreta y ejecuta la expresión contenida en la cadena de caracteres "0.1+0.2"
Lo cual conlleva las siguientes acciones :
- Análisis lexicográfico que divide la cadena en 3 símbolos(tokens) :
0.1 , + y 0.2
Análisis sintáctico que, por ejemplo (puede ser de muchas formas), crea una estructura de árbol sintáctico:
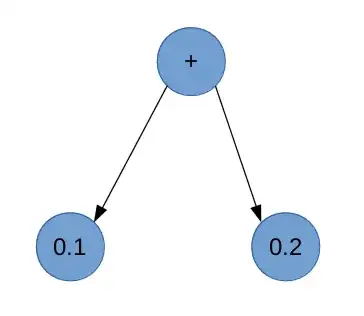
Análisis semántico que convierte 0.1 al valor más cercano que es representable con el tipo de datos elegido, en este caso el implícito. Y lo mismo con 0.2 . Aquí está una fuente de error. El programa no va a manejar el valor 0.1 sino aquel más cercano que es representable en el tipo de datos elegido, que en javascript es doble precisión tal y como se especifica en standard IEEE 754. Y en ese formato 0.1 no es posible representarlo exáctamente, con lo que hay un pequeño error.
- Ejecución. Que suma los dos valores y convierte el resultado al más cercano que es representable. Esto es otra fuente de errores.
- Impresión. Imprimir una representación visual del valor de suma obtenido. Puede ocurrir que el resultado sea correcto (por ejemplo 0.125+0.125=0.25) pero que por el formato de impresión elegido se impriman menos decimales (0.2) . En este caso el ordenador ha calculado la solución exacta pero ha mostrado una aproximación. Y también puede ocurrir que el resultado sea inexacto (por ejemplo 0.1+0.2=0.30000000000000004) pero que por el formato de impresión elegido se omitan decimales dando apariencia de resultado exacto (.3) pese a que el valor de suma almacenado en el ordenador sea ligeramente inexacto.
Conclusiones
Es posible hacer cálculos exactos en un ordenador. Hay programas y lenguajes específicos para ello.
En los lenguajes de programación de propósito general, como C++, Java o Javascript, se hacen cálculos aproximados por defecto, por cuestiones de rendimiento y porque es suficiente para múltiples aplicaciones. En estos lenguajes también es posible hacer cálculos exactos pero hay que utilizar las librerías y/o elementos del lenguaje apropiados.