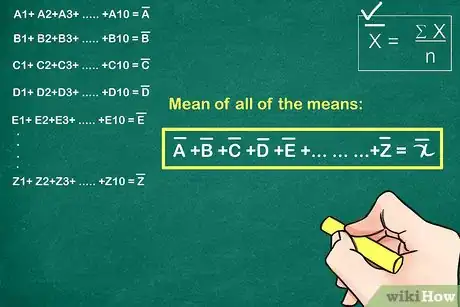Cómo crear una tabla de control

Información del autor

Los gráficos de control son una forma eficiente de analizar los datos de rendimiento para evaluar un proceso. Los gráficos de control tienen muchos usos, ya que pueden ser utilizados en la fabricación de maquinaria para comprobar si se producen productos dentro de determinadas condiciones. Además, tienen muchas aplicaciones sencillas, por ejemplo, los profesores las utilizan para evaluar los resultados de los exámenes o la evolución de los alumnos. Para crear un gráfico de control, es necesario disponer de Excel, verás cómo este programa va a simplificar los procesos y, a cambio, tendrás más tiempo para hacer otras cosas.

Pasos

1
Comprueba que tus datos cumplen todos los criterios:
- Los datos generalmente se distribuyen normalmente en torno a una media (promedio).
  - En el siguiente ejemplo, una compañía de la botellas llena sus botellas hasta los 16 oz (de media), ellos están evaluando si el proceso está "en control". La cantidad que sobrepasa esos 16 onzas se distribuye en torno a la media.
- Las medidas tienen que ser independientes entre sí.
  - En el ejemplo, las mediciones están en subgrupos. Los datos de los subgrupos debe ser independientes del número de medición; cada punto de datos tendrá un subgrupo y un número de mediciones.
2
Encuentra la media de cada subgrupo
- Para encontrar la media, añade todas las mediciones en el subgrupo y divídelas por el número de mediciones en el subgrupo.
  - En el ejemplo, hay 20 subgrupos y en cada subgrupo hay 4 mediciones.
3
Encuentra la media de todas las medias obtenidas en el paso anterior (X).
- Esto te proporcionará la media general de todos los puntos de datos.
- La media general será la línea central en el gráfico (CL), que es 13,75 para nuestro ejemplo.
4
Calcula la desviación estándar (S) de los puntos de datos (ver consejos).
5
Calcula los límites de control superior e inferior (UCL, LCL) utilizando la siguiente fórmula:
- - UCL = CL + 3*S
  - LCL = CL – 3*S
  - La fórmula representa 3 desviaciones estándar por encima y 3 desviaciones estándar por debajo de la media, respectivamente.
6
Consulta la siguiente tabla con los pasos 7 a 10.
7
Dibuja la línea de cada derivación.
- En el ejemplo anterior, hay una línea trazada en una, dos y tres desviaciones estándar (Sigma) que se distancian de la media.
  - Zona C es 1 sigma lejos de la media (verde).
  - Zona B es 2 sigma lejos de la media (amarillo).
  - Zona A es 3 sigma lejos de la media (red).
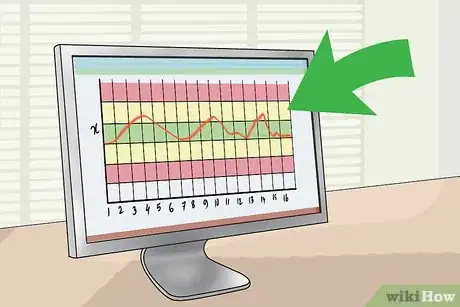
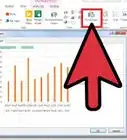
8
Gráfico de la barra X del gráfico de control. Haz la gráfica de los medias de los subgrupos (eje X) frente a las mediciones (eje Y). Tu gráfico debería parecerse a algo como esto:
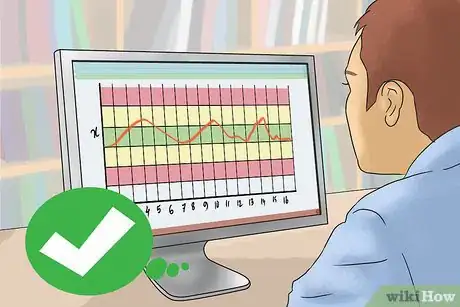
9
Evaluar el gráfico para ver si el proceso está fuera de control. El gráfico estará fuera de control si:
- Cualquier punto cae fuera de la zona roja (por encima o por debajo de la línea de 3-sigma).
- 8 puntos consecutivos caen en un lado de la línea central.
- 2 o 3 puntos consecutivos caen dentro de la zona A.
- 4 o 5 puntos consecutivos caen dentro de la zona A y / o zona B.
- 15 puntos consecutivos se encuentran dentro de la Zona C.
- 8 puntos consecutivos y no en la zona C.
10
Este es el estado si el sistema está en el control o fuera de control.

Consejos

Utiliza Excel cuando se creen los gráficos, porque es ahí donde has construido funciones (que se muestra a continuación) que acelerará tus cálculos.
Los comandos de Excel que harán más fácil analizar los datos son los siguientes:

La desviación estándar: = STDEV (puntos de datos)

Media: = PROMEDIO (puntos de datos)
Practica con ejemplos cotidianos. Por ejemplo, si un profesor está mirando la variación en las calificaciones de los estudiantes, podrían utilizar un gráfico de control. Los subgrupos serían los estudiantes y las medidas sería la forma en que realiza en cada prueba. Al crear un gráfico de control se podría ver cómo evolucionan los estudiantes y cuales están más cerca de la media. Todos los estudiantes que lo hacen muy bien o que sacan malas notas se destacaría notablemente en este tipo de gráficos.

Advertencias

Los gráficos de control son (en general) para bases de datos en los que la información está distribuida normalmente. En la práctica, sin embargo, son razonablemente robusto para datos no normales.
Para realizar algunos gráficos, POR EJEMPLO, el gráfico C, los datos probablemente no tendrán una distribución normal.
Mueve los gráficos de intervalos (de uso frecuente con la Tabla de las personas, también conocido como gráfico de la X o I) o utiliza diferentes reglas de interpretación para hacer frente a la fuerte no-normalidad de movimiento de datos del área de distribución.
La barra X del gráfico, como el que se explica más arriba, es donde se hallan los valores individuales. Como se explica por el teorema del límite central, los medios tienden a tener una distribución normal, incluso si los datos subyacentes no lo son.