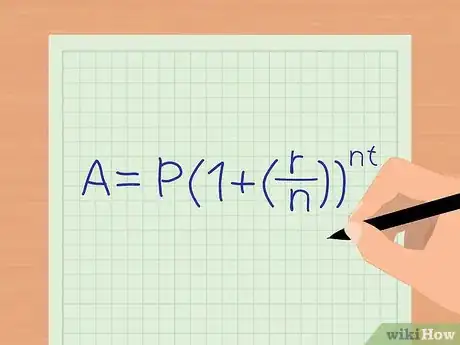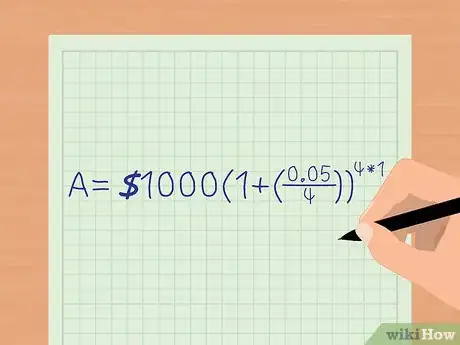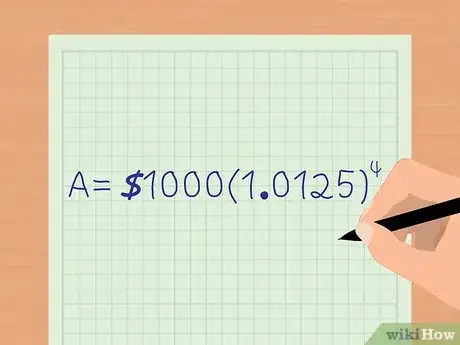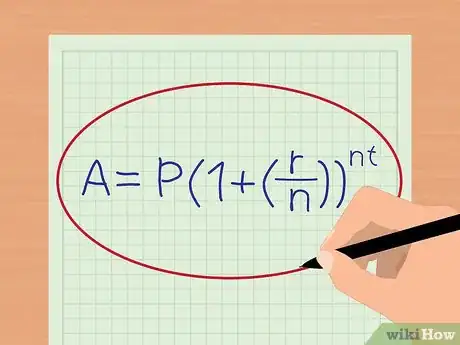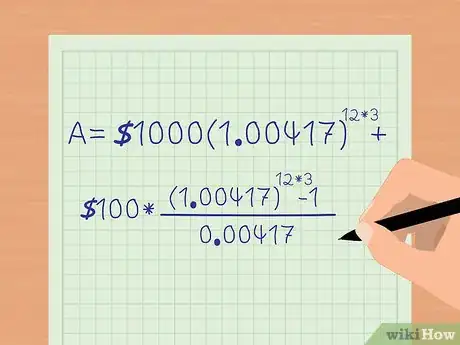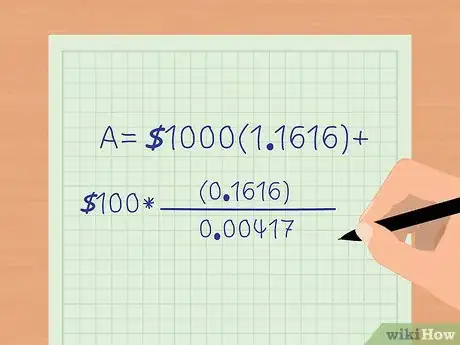Comment calculer les intérêts bancaires d'une épargne

Les intérêts sont parfois très faciles à calculer, lorsqu’il suffit de multiplier le taux d’intérêt par le montant du capital, mais les choses sont rarement aussi simples. Il arrive par exemple fréquemment que des comptes d’épargne rapportent des intérêts composés mensuellement à partir d’un taux d’intérêt annuel. Tous les mois, une fraction des intérêts annuels est calculée et ajoutée à votre solde, ce qui modifie donc le calcul pour le mois suivant. Ce mode de calcul correspond mathématiquement à une suite et le meilleur moyen de trouver de combien vous disposerez au bout du compte est d’utiliser la formule des intérêts composés. Un certain nombre de conseils vous seront utiles pour comprendre les tenants et les aboutissants d’une telle opération.

Méthode 1

Méthode 1 sur 3:
Calculer les intérêts composés

1
Notez la formule des intérêts composés. La formule qui permet de trouver les effets des intérêts composés sur le solde d’un compte est la suivante : $A=P(1+({\frac {r}{n}}))^{n*t}$ $A=P(1+({\frac {r}{n}}))^{{n*t}}$ .
- (P) correspond au montant du capital de départ, (r) au taux d’intérêt annuel et (n) est le nombre de fois où mes intérêts sont composés dans l’année. (A) représente le solde du compte en tenant compte des intérêts versés.
- (t) correspond à la période de temps au cours de laquelle les intérêts s’accumulent. Elle doit être en corrélation avec le taux que vous utilisez dans vos calculs. Par exemple, si le taux d’intérêt est annuel, (t) doit être un nombre / une portion de l’année). Pour déterminer quel nombre utiliser pour compter les années écoulées au cours d’une période de temps donnée, divisez simplement le nombre de mois par 12 ou le nombre de jours par 365.
2
Trouvez les valeurs. Plongez-vous dans le contrat qui vous a été fourni quand vous avez ouvert votre compte épargne ou bien contactez votre banquier pour connaitre les valeurs que vous allez insérer dans l’équation.
- Le capital (P) peut représenter soit la somme initialement versée sur le compte, soit le solde actuel de celui-ci à partir duquel vous désirez calculer des intérêts futurs.
- Le taux d’intérêt (r) doit être exprimé sous forme décimale. Cela veut dire que pour un taux de 3 %, on écrira 0,03. Pour arriver à ce chiffre, il vous suffit de prendre le taux et de le diviser par 100.
- La valeur de (n) sera le nombre de fois par an où les intérêts sont calculés et ajoutés au solde (c’est-à-dire composés). En général, les intérêts sont composés soit mensuellement (n=12), soit trimestriellement (n=4), soit annuellement (n=1). En fonction des termes de votre contrat, il est possible qu’il en soit autrement ^{[1]
  X
  Source de recherche}.
- La valeur moyenne du taux d’intérêt pour les comptes d’épargne tourne habituellement autour de 1,8 % .
3
Intégrez les valeurs à la formule. Une fois que vous avez déterminé le montant correspondant à chaque variable, placez-les dans la formule pour calculer le montant perçu au cours de la période donnée. En prenant par exemple P=1 000 €, r=0,05 (5 %), n=4 (pour des intérêts composés trimestriellement) et t=1 an, nous obtenons l’équation suivante : $A=1000(1+({\frac {0,05}{4}}))^{4*1}$ $A=1000(1+({\frac {0,05}{4}}))^{{4*1}}$ .
- La formule fonctionne de la même manière pour des intérêts composés quotidiennement. Il suffit de remplacer, pour la valeur de (n), le 4 par 365 ^{[2]
  X
  Source de recherche}.
4
Faites le calcul. Maintenant que tous les nombres sont en place, il ne vous reste plus qu’à résoudre l’équation. Commencez par simplifier certaines parties, par exemple en divisant le taux annuel par le nombre d’occurrences de la composition, pour obtenir le taux périodique (dans notre cas, cela donne ${\frac {0,05}{4}}=0,0125$ ${\frac {0,05}{4}}=0,0125$ ). Vous pouvez aussi résoudre $n*t$ $n*t$ , qui pour nous est simplement $4*1$ $4*1$ . Vous aboutissez à $A=1000(1+(0,0125))^{4}$ $A=1000(1+(0,0125))^{{4}}$ .
- Vous pouvez encore simplifier en calculant ce qui se trouve entre parenthèses : $1+0,0125=1,0125$ . Le résultat sera : $1+0,0125=1,0125$ .
5
Résolvez l’équation. Ensuite, passez le résultat de l’étape précédente à l’exposant 4 (c’est-à-dire que vous devez faire $1,0125*1,0125*1,0125*1,0125$ $1,0125*1,0125*1,0125*1,0125$ ). Vous arrivez à $1,051$ $1,051$ . L’équation est désormais très simple : $A=1000(1,051)$ $A=1000(1,051)$ . On multiplie ces deux nombres et on obtient $A=1051$ $A=1051$ . Il s’agit du solde de votre compte au bout d’un an avec un taux d’intérêt de 5 % et des intérêts crédités trimestriellement.
- Vous pouvez remarquer que ce résultat est légèrement supérieur à $1000*5\ \%$ , qui est le solde auquel vous auriez pu vous attendre au vu de la façon dont le taux annuel est présenté de prime abord. C’est pour cela qu’il est très important de savoir comment sont composés les intérêts !
- Pour savoir combien vous avez gagné, faites la différence entre A et P : votre gain est de : $1051-1000=51$ €.
Publicité

Méthode 2

Méthode 2 sur 3:
Calculer les intérêts avec des apports réguliers

1
Servez-vous de la formule de l’épargne cumulée. Vous pouvez également calculer combien vous percevez d’intérêts pour un compte sur lequel vous faites des versements réguliers. Cela vous sera utile si vous économisez chaque mois une somme que vous placez en épargne. L’équation est la suivante : $A=P(1+({\frac {r}{n}}))^{nt}+PMT*{\frac {(1+{\frac {r}{n}})^{nt}-1}{\frac {r}{n}}}$ $A=P(1+({\frac {r}{n}}))^{{nt}}+PMT*{\frac {(1+{\frac {r}{n}})^{{nt}}-1}{{\frac {r}{n}}}}$ ^{[3]
X
Source de recherche}.
- Pour aborder le calcul plus facilement, il est judicieux de séparer les intérêts composés réalisés grâce au capital de départ de ceux perçus grâce aux apports mensuels (PMT signifie « paiement »). Commencez par calculer les intérêts du capital grâce à la formule des intérêts d’épargne cumulés.
- Comme évoqué précédemment, il faut savoir que cette formule sert à calculer les intérêts perçus sur des comptes bancaires qui bénéficient de dépôts mensuels et dont les intérêts sont composés quotidiennement, mensuellement ou trimestriellement ^{[4]
  X
  Source de recherche}.
2
Utilisez la deuxième partie de la formule. Elle sert à calculer les intérêts sur vos apports. (PMT) représente le montant de vos versements mensuels.
3
Identifiez les variables. Consultez vos relevés bancaires ou votre contrat pour connaitre les données suivantes : le montant du capital « P », le taux d’intérêt annuel « r » et le nombre de périodes dans l’année « n ». Si vous ne parvenez pas à les trouver, téléphonez à votre banquier pour lui demander de vous communiquer ces informations. « t » représente le nombre d’années ou la fraction d’année sur laquelle porte le calcul et « PMT » correspond à l’apport versé tous les mois. « A » est le solde du compte à la fin de la période et après versement de tous les apports.
- Le capital (P) peut représenter soit la somme initialement versée sur le compte, soit le solde actuel de celui-ci à partir duquel vous désirez calculer des intérêts futurs.
- Le taux d’intérêt « r » est le taux annuel des intérêts du compte. Il doit être exprimé sous forme décimale. Cela signifie que pour un taux de 3 %, on écrira 0,03. Pour arriver à ce chiffre, il vous suffit de prendre le taux et de le diviser par 100.
- La valeur de (n) sera le nombre de fois par an où les intérêts sont calculés et ajoutés au solde. (n) vaudra 365 si les intérêts sont composés quotidiennement, 12 s’ils le sont mensuellement et 4 s’ils le sont trimestriellement.
- La valeur de « t » correspond au nombre d’années qui vous avez choisi pour calculer vos futurs intérêts. Il peut s’agir soit d’un nombre entier, soit d’une fraction si vous vous basez sur une période inférieure à un an. Ce sera par exemple 0,0833 pour un mois ^{[5]
  X
  Source de recherche} (1/12).
4
Insérez les valeurs dans la formule. Prenons un exemple pour lequel P=1 000 €, r=0,05 (5 %), n=12 (intérêts composés mensuellement), t=3 ans et PMT=100 €. Nous obtenons : $A=1000(1+({\frac {0,05}{12}}))^{12*3}+100*{\frac {(1+{\frac {0,05}{12}})^{12*3}-1}{\frac {0,05}{12}}}$ .
5
Simplifiez l’équation. Commencez par la partie ${\frac {r}{n}}$ , dans laquelle il est possible de diviser le taux 0,05 par 12. Vous arrivez à $A=1000(1+(0,00417))^{12*3}+100*{\frac {(1+0,00417)^{12*3}-1}{0,00417}}$ . Vous pouvez ensuite simplifier en ajoutant un au taux entre parenthèses. L’équation sera alors : $A=1000(1,00417))^{12*3}+100*{\frac {(1,00417)^{12*3}-1}{0,00417}}$
6
Calculez la partie avec une puissance. Commencez par effectuer l’opération qui se trouve sous la puissance, c’est-à-dire $n*t$ , ce qui nous donne $12*3=36$ . Simplifiez ensuite en traitant l’exposant : $A=1000(1,1616)+100*{\frac {1,1616-1}{0,00417}}$ . Soustrayez le 1, il reste $A=1000(1,1616)+100*{\frac {0,1616}{0,00417}}$ .
7
Terminez l’opération. Faites la multiplication de la première partie, qui donne 1 616 €. Résolvez la deuxième partie en divisant le numérateur de la fraction par son dénominateur : ${\frac {0,1616}{0,00417}}=38,753$ . Multipliez ce résultat par le montant des versements (100 € dans notre cas). Notre équation est désormais : $A=1616+3875,30=5491,30$ . Avec les conditions que nous avions choisies, le solde final du compte serait $5491,30$ €.
8
Calculez le montant des intérêts. Avec cette équation, les intérêts gagnés correspondent au solde total (A) moins le montant du capital (P) et moins le nombre de versements multiplié par leur montant (PMT*n*t). Donc, pour notre exemple, les intérêts sont de : $5491,30-1000-100(12*3)$ et donc $5491,30-1000-3600=891,30$ ^{[6]
X
Source de recherche}.

Publicité

Méthode 3

Méthode 3 sur 3:
Se servir d’une feuille de calcul pour les intérêts composés

1
Ouvrez une nouvelle feuille de calcul. Excel ou tout autre programme proposant des feuilles de calcul (comme Google Sheets par exemple) vous permettra de gagner du temps. En effet, il vous évitera de devoir faire vous-même les opérations et pourra même vous offrir des fonctions prêtes à l’emploi pour calculer vos intérêts composés.
2
Nommez vos variables. Quand on se sert d’une feuille de calcul, il est essentiel d’être bien organisé pour que les choses soient aussi claires que possible. Commencez par remplir une colonne de cellules dans lesquelles vous renseignerez les informations de base que vous intègrerez par la suite à l’équation. Indiquez notamment le taux d’intérêt, le capital, la période, les versements.
3
Tapez vos données. Vous devez maintenant renseigner toutes les informations propres à votre compte bancaire dans la colonne juste à côté. Non seulement cela permet de rendre la feuille de calcul bien plus facile à lire et à comprendre, mais cela vous laisse en plus la possibilité de modifier par la suite l’une des valeurs pour voir ce que vous pourriez gagner avec d’autres types de contrats.
4
Entrez votre équation. L’étape suivante consiste à créer votre propre formule à partir de la formule simplifiée des intérêts composés ( $A=P(1+({\frac {r}{n}}))^{n*t}$ ) ou à partir de sa version complète ( $A=P(1+({\frac {r}{n}}))^{nt}+PMT*{\frac {(1+{\frac {r}{n}})^{nt}-1}{\frac {r}{n}}}$ ), qui prend en compte des versements réguliers. Vous pouvez la placer dans n’importe quelle cellule vide. N’oubliez pas que vous devez toujours commencer par le signe « = » et écrire selon les règles mathématiques habituelles (mettez des parenthèses si nécessaire). Plutôt que de nommer les variables avec des lettres comme (P) ou (n), tapez le nom de la cellule dans laquelle vous avez renseigné la donnée correspondante. Vous pouvez aussi cliquer dessus pour qu’elle apparaisse directement à l’endroit désiré de votre équation.
5
Servez-vous des fonctions financières. Excel propose également un certain nombre de fonctions financières qui peuvent vous aider. Vous pouvez notamment utiliser la fonction VC, qui permet de calculer le solde futur d’un compte en fonction d’un certain nombre de variables que vous connaissez désormais parfaitement. Pour accéder à cette fonction, il suffit de se placer dans n’importe quelle cellule vide et de taper « =VC( ». Dès que vous aurez tapé la première parenthèse, Excel ouvrira automatiquement une fenêtre pour vous guider afin que vous puissiez intégrer les bons paramètres à la fonction ^{[7]
X
Source de recherche}.
- Cette fonction est destinée à calculer le montant d’un remboursement avec ses intérêts et non à calculer le montant des intérêts que l’on gagne avec un compte d’épargne. C’est pourquoi le résultat sera toujours un nombre négatif. Pour corriger ce problème, il vous suffit de taper $=-1*FV($ .
- La fonction VC tient compte de données similaires à celles vues précédemment et qui seront présentées séparées par des virgules, mais qui ne sont pas parfaitement identiques aux nôtres. Ici par exemple, « taux » désigne $r/n$ (c’est-à-dire le taux d’intérêt annuel divisé par n). Le résultat sera calculé automatiquement dans la parenthèse de la fonction VC.
- Le paramètre « npm » correspond à la variable $n*t$ : le nombre total de périodes sur la durée considérée fois le nombre total de paiements. En d’autres termes, si votre PMT n’est pas égal à 0, la fonction VC partira du principe que vous versez ce PMT à chaque échéance, sans exception, tout au long de la durée définie par « npm ».
- Remarque : cette fonction est en général utilisée pour calculer comment le capital d’un prêt immobilier est remboursé au fil du temps grâce à des paiements réguliers. Par exemple, si vous prévoyez de verser de l’argent tous les mois pendant 5 ans, « npm » sera égal à 60 (5 ans*12 mois).
- PMT est le montant de votre apport régulier sur toute la durée prise en compte (un apport par n).
- « Va » (pour « valeur actuelle ») est le solde de départ, votre capital de base.
- Vous pouvez laisser le champ de la dernière variable, « type », vide. Lorsqu’il n’est pas renseigné, la formule considère automatiquement qu’il vaut 0.
- La fonction VC permet de faire des calculs de base en entrant des paramètres. Par exemple, utilisée correctement, cette fonction pourra vous donner : $-1*FV(0,05/12,12,100,5000)$ . Cela signifie que vous bénéficiez sur votre compte d’un taux d’intérêt annuel de 5 %, qu’ils sont composés mensuellement pendant 1 an, que vous y versez tous les mois 100 € et que votre capital de départ était de 5 000 €. Vous verrez apparaitre dans la cellule le résultat de cette équation. Au bout d’un an, votre solde sera de 6 483,70 €.
Publicité

Conseils

Il est également possible, bien qu’un peu plus complexe, de calculer le montant des intérêts composés pour un compte sur lequel on effectue des versements irréguliers. Il faudra dans ce cas employer une méthode qui consiste à calculer séparément les intérêts dont on bénéficie pour chacun des apports (avec la même équation que précédemment). Pour être certain de ne pas faire d’erreur, il vaut mieux se servir d’une feuille de calcul.
Vous pouvez aussi avoir recours à un calculateur de taux de rendement annuel en ligne. Faites une recherche avec les termes « calculateur de taux de rendement annuel » ou bien « calculateur annuel d’intérêt » pour obtenir de nombreux services gratuits.
Les banques en ligne ont tendance à offrir des taux d’intérêt plus élevés que ceux proposés par les banques traditionnelles.