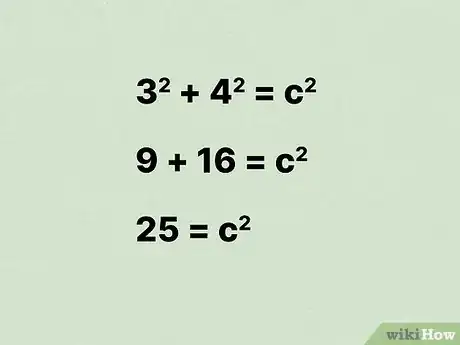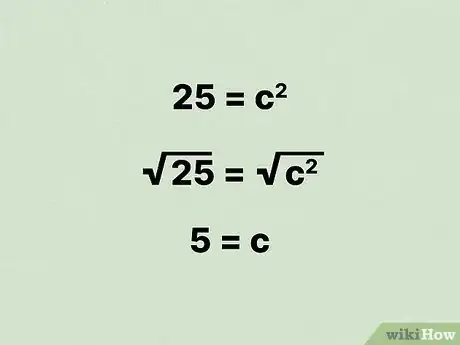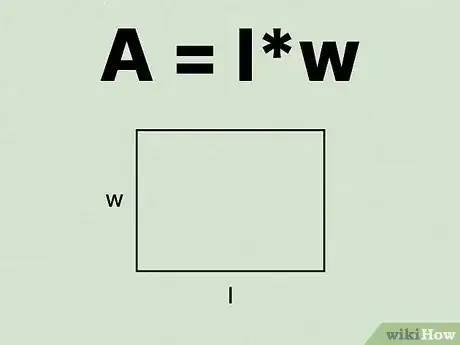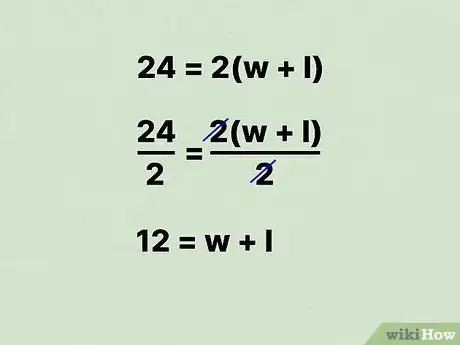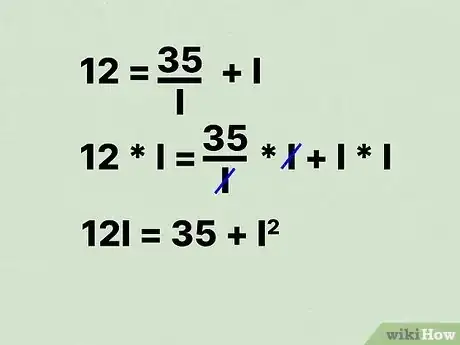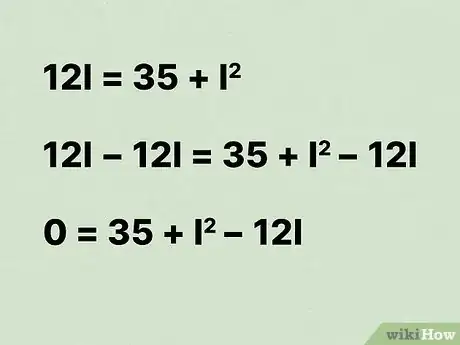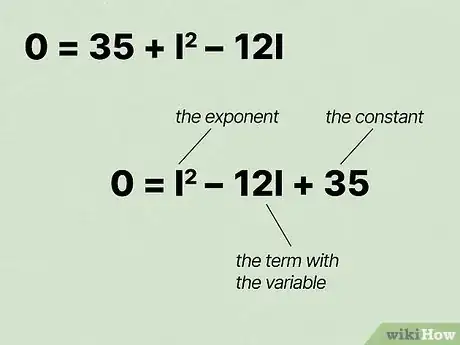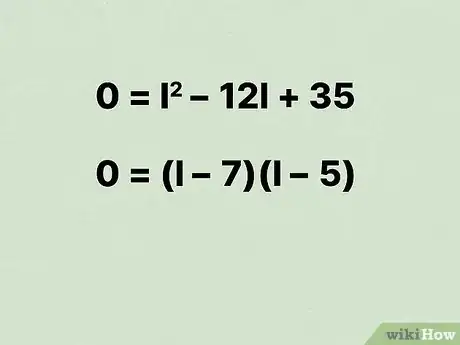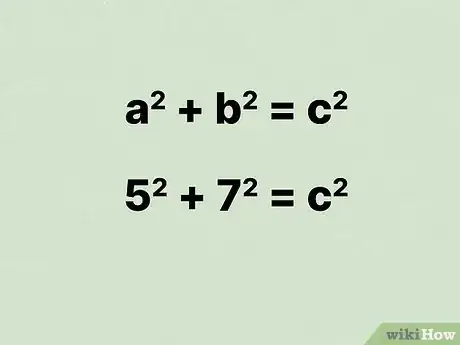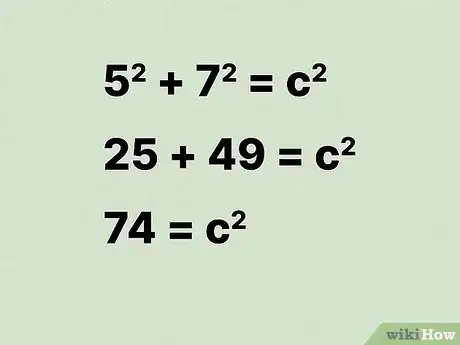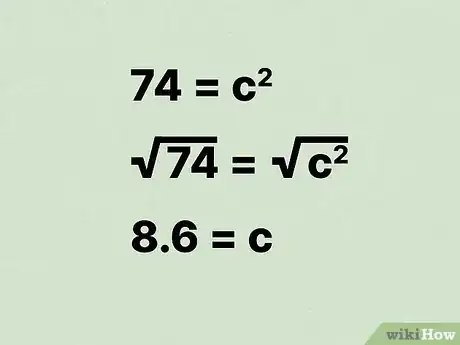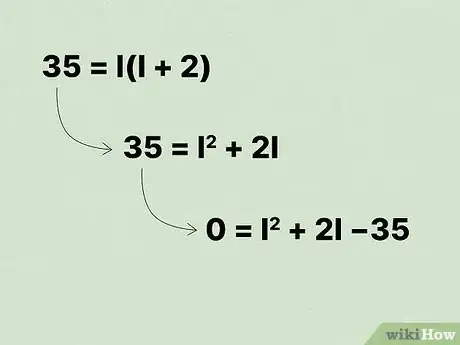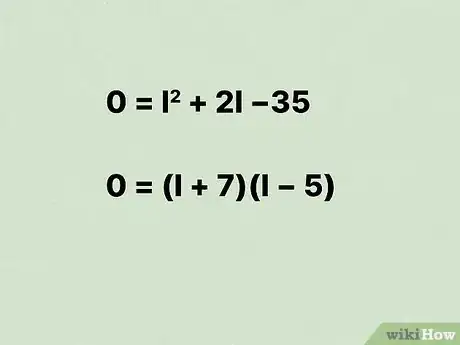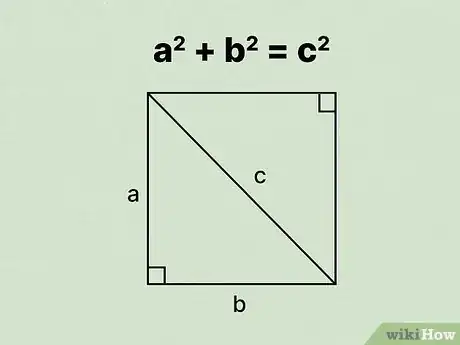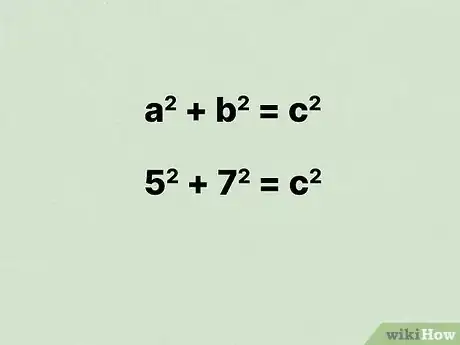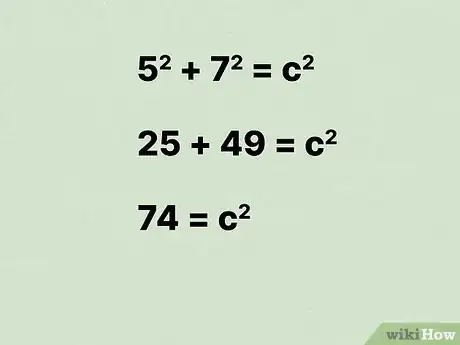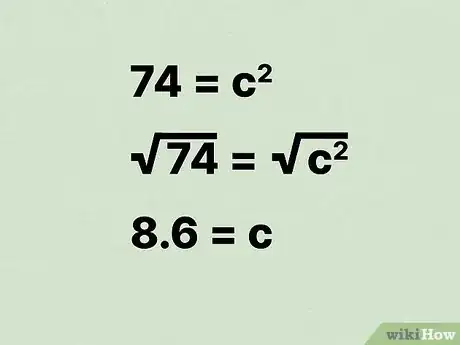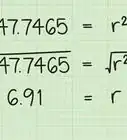Comment calculer la diagonale d’un rectangle

Coécrit par David Jia

Dans un rectangle, la diagonale est la ligne droite qui relie les deux sommets opposés de la figure ^{[1]
X
Source de recherche}. Ainsi, on peut dire qu'un rectangle a deux diagonales identiques de même longueur ^{[2]
X
Source de recherche}. En connaissant la valeur des longueurs des côtés qui composent un rectangle, vous pouvez trouver facilement la valeur de la diagonale en utilisant le théorème de Pythagore, étant donné qu’une diagonale divise un rectangle en deux triangles. Si vous ne connaissez pas cette mesure, mais disposez d’autres informations, telles que la superficie et le périmètre ou la relation entre les côtés, vous pouvez utiliser quelques étapes supplémentaires pour trouver la longueur et la largeur de votre figure, et de là, il vous serait possible d'utiliser le théorème de Pythagore pour calculer la longueur la diagonale.

Méthode 1

Méthode 1 sur 3:

Utiliser la longueur et la largeur

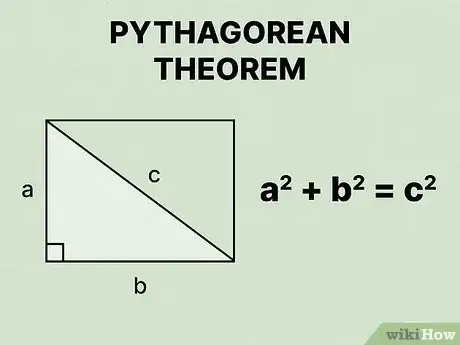
1
Définissez le théorème de Pythagore. Cette formule est la suivante : $a^{2}+b^{2}=c^{2}$ $a^{{2}}+b^{{2}}=c^{{2}}$ , où $a$ $a$ et $b$ $b$ représentent les côtés d'un triangle rectangle, et $c$ $c$ est son hypoténuse ^{[3]
X
Source de recherche}.
- Vous devez utiliser ce théorème parce que la diagonale d'un rectangle divise celui-ci en deux triangles congruents ^{[4]
  X
  Source de recherche}. La longueur et la largeur représentent les côtés du triangle, alors que la diagonale représente son hypoténuse.
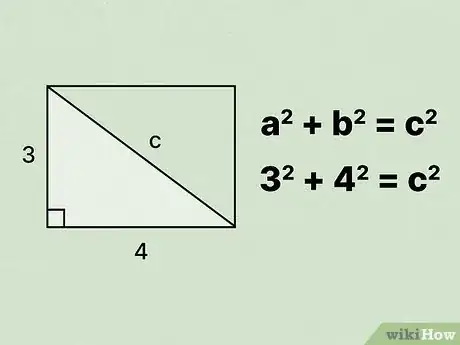
2
Remplacez ces grandeurs dans la formule. Elles devraient être données, ou vous pouvez les mesurer à l’aide d’une règle ou d’un mètre. Assurez-vous de remplacer les valeurs des grandeurs $a$ $a$ et $b$ $b$ .
- Par exemple, si la longueur de votre rectangle est de 4 cm et la largeur mesure 3 cm, la formule sera la suivante : $4^{2}+3^{2}=c^{2}$ .
3
Mettez au carré ces deux grandeurs et additionnez-les. N’oubliez pas qu’élever au carré un nombre revient à le multiplier par lui-même.
- Dans notre exemple, on obtient :
  $4^{2}+3^{2}=c^{2}$
  $16+9=c^{2}$
  $25=c^{2}$ .
4
Calculez la racine carrée de chaque terme de l'équation. La meilleure façon d'effectuer ce calcul c’est d'utiliser une calculatrice. Si vous ne disposez pas d’une calculatrice scientifique, vous pouvez faire le calcul en ligne ^{[5]
X
Source de recherche}. De cette façon, vous obtiendrez la valeur de $c$ $c$ qui représente l'hypoténuse du triangle, ainsi que la diagonale.
- Dans notre exemple, vous aurez :
  $25=c^{2}$
  ${\sqrt {25}}={\sqrt {c^{2}}}$
  $5=c$
  Par conséquent, la diagonale d'un rectangle ayant une largeur de 3 cm et une longueur de 4 cm mesure 5 cm.
Publicité

Méthode 2

Méthode 2 sur 3:

Utiliser la superficie et le périmètre

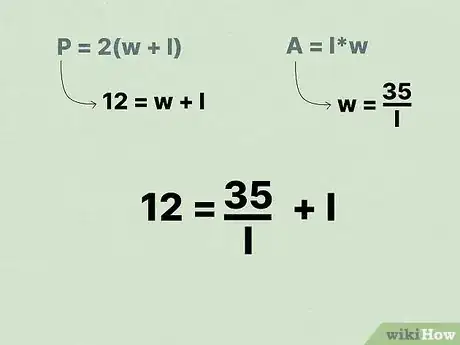
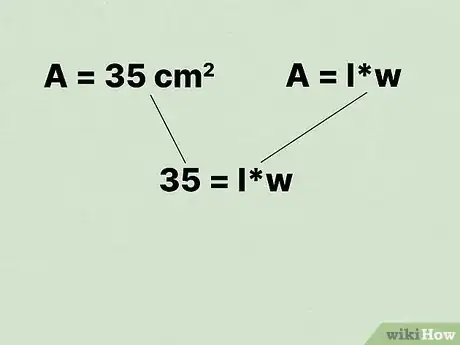
1
Écrivez la formule pour calculer l'aire d'un rectangle. La formule est la suivante : $A=Ll$ , où $A$ est l'aire de la figure, $L$ la longueur du rectangle, et $l$ la largeur ^{[6]
X
Source de recherche}.
2
Remplacez dans la formule l’aire de votre figure. Assurez-vous de remplacer cette valeur par la variable $A$ $A$ .
- Par exemple, si l’aire du rectangle est de 35 centimètres carrés, la formule sera la suivante : $35=Ll$ .
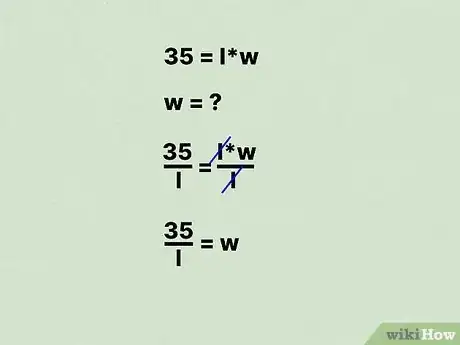
3
Réarrangez la formule pour calculer la valeur de $L$ . Pour ce faire, divisez les deux côtés de l'équation par $l$ $l$ . Une fois cette valeur calculée, mettez-la de côté, vous l’utiliserez plus tard pour calculer le périmètre du rectangle.
- Dans notre exemple, vous obtiendrez :
  $35=Ll$
  ${\frac {35}{l}}=L$ .
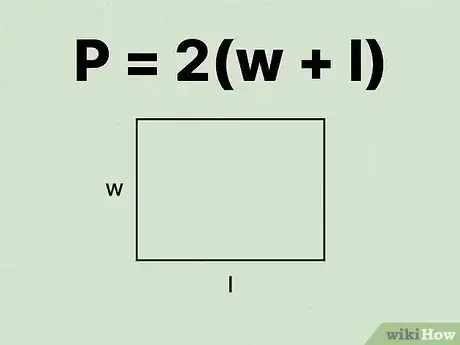
4
Écrivez la formule pour calculer le périmètre d'un rectangle. La formule en question est la suivante $P=2(L+l)$ , où $L$ représente la longueur du rectangle, et $l$ la largeur ^{[7]
X
Source de recherche}.
5
Remplacez les valeurs connues pour calculer le périmètre. Assurez-vous de remplacer la variable $P$ $P$ .
- Supposons que nous avons un rectangle dont le périmètre est égal à 24 cm, la formule va se présenter comme suit : $24=2(L+l)$ .
6
Divisez les deux éléments de l'équation par 2. Ainsi, vous obtiendrez la valeur de $L+l$ $L+l$ .
- Dans notre exemple, on obtient :
  $24=2(L+l)$
  ${\frac {24}{2}}={\frac {2(L+l)}{2}}$
  $12=L+l$ .
7
Remplacez la variable $L$ dans l'équation. Utilisez la valeur trouvée en réarrangeant la formule de la surface.
- Dans notre exemple, vous verrez que ${\frac {35}{l}}=L$ . Remplacez à présent la valeur de $L$ dans la formule du périmètre. On obtient ceci :
  $12=L+l$
  $12={\frac {35}{l}}+l$ .
8
Simplifiez l'équation en faisant disparaitre la fraction. Pour ce faire, multipliez les deux termes de l'équation par $l$ $l$ .
- Dans notre exemple, on obtient :
  $12={\frac {35}{l}}+l$
  $12\times l=({\frac {35}{l}}\times l)+(l\times l)$
  $12l=35+l^{2}$ .
9
Supposez que l'équation est égale à 0. Pour cela, vous devez soustraire le terme du premier degré des deux éléments de l'équation.
- Dans notre exemple, on obtient :
  $12l=35+l^{2}$
  $12l-12l=35+l^{2}-12l$
  $0=35+l^{2}-12l$ .
10
Réorganisez l'équation par ordre des termes. Autrement dit, le terme possédant un exposant vient en premier, suivi par le terme ne possédant aucun exposant (la variable), puis la constante. Durant cette étape, faites très attention aux signes + et -. Vous devriez remarquer à présent que votre expression est sous forme d’une équation du second degré.
- Dans notre exemple, l'équation d'origine, $0=35+l^{2}-12l$ devient $0=l^{2}-12l+35$ .
11
Factorisez votre équation du second degré. Pour plus d’instructions à ce sujet, consultez cet article.
- Par exemple, l'équation $0=l^{2}-12l+35$ peut être factorisée comme suit : $0=(l-7)(l-5)$ .
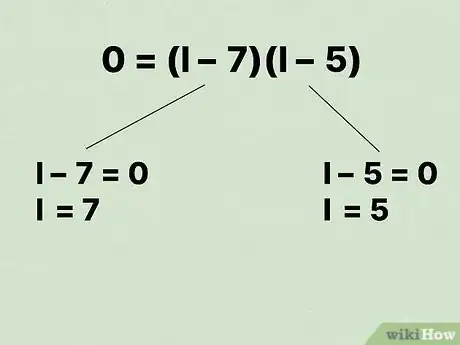
12
Déterminez la valeur de la grandeur $l$ . Pour ce faire, supposez que chaque terme de l'équation est égal à zéro, puis faites les calculs. Vous trouverez deux solutions, ou deux racines. Étant donné que nous étudions un rectangle, les deux racines représenteront les valeurs de la largeur et de la longueur du rectangle.
- Dans notre exemple, on obtient :
  $0=(l-7)$
  $7=l$
  Et
  $0=(l-5)$
  $5=l$ .
  Forcément, la longueur et la largeur du rectangle font respectivement 7 cm et 5 cm.
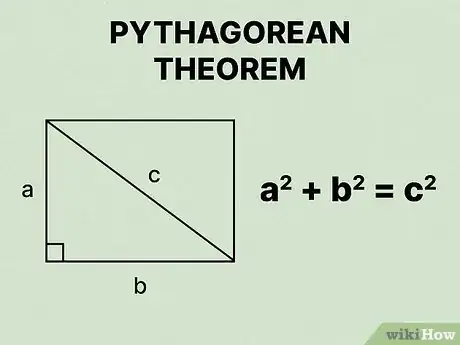
13
Définissez la formule du théorème de Pythagore. Cette formule est la suivante $a^{2}+b^{2}=c^{2}$ $a^{{2}}+b^{{2}}=c^{{2}}$ , où $a$ $a$ et $b$ $b$ représentent les côtés d’un triangle rectangle, et $c$ $c$ est l’hypoténuse de celui-ci ^{[8]
X
Source de recherche}.
- Dans ce cas, vous pouvez utiliser le théorème de Pythagore, car la diagonale d'un rectangle divise celui-ci en deux triangles rectangles congruents ^{[9]
  X
  Source de recherche}. La longueur et la largeur représentent les côtés du triangle, alors que la diagonale représente l’hypoténuse.
14
Remplacez la largeur et la longueur dans la formule. Peu importe quelle valeur vous utilisez pour chaque variable, vous obtiendrez le même résultat.
- Par exemple, si vous trouvez que la longueur et la largeur de votre rectangle sont respectivement de 7 et 5 cm, la formule sera la suivante : $5^{2}+7^{2}=c^{2}$ .
15
Mettez au carré ces deux grandeurs et additionnez-les. N’oubliez pas qu’élever au carré un nombre revient à le multiplier par lui-même.
- Par exemple :
  $5^{2}+7^{2}=c^{2}$
  $25+49=c^{2}$
  $74=c^{2}$ .
16
Calculez la racine carrée de chaque terme de l'équation. La meilleure façon d'effectuer ce calcul c’est d'utiliser une calculatrice scientifique. Si vous n'en disposez pas, vous pouvez utiliser une calculatrice en ligne ^{[10]
X
Source de recherche}. De cette façon, vous obtiendrez la valeur de $c$ $c$ qui représente l'hypoténuse du triangle, ainsi que la diagonale.
- Par exemple :
  $74=c^{2}$
  ${\sqrt {74}}={\sqrt {c^{2}}}$
  $8,6024=c$
  Par conséquent, la diagonale d'un rectangle ayant une aire de 35 cm et un périmètre de 3 cm est de 8,6 cm.
Publicité

Méthode 3

Méthode 3 sur 3:

Utiliser l’aire et les relations entre les cotés d'un rectangle

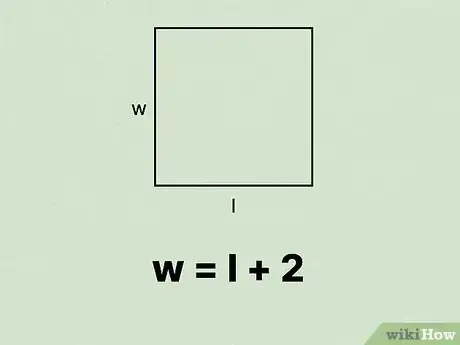
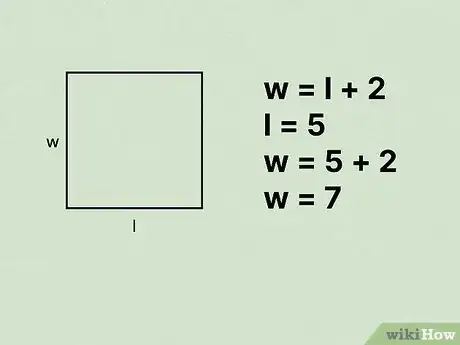
1
Écrivez l'équation exprimant la relation entre les côtés du rectangle ^{[11]
X
Source de recherche}. Vous pouvez choisir d'isoler la longueur ( $L$ $L$ ) ou la largeur ( $l$ $l$ ). Réservez cette formule pour une utilisation ultérieure.
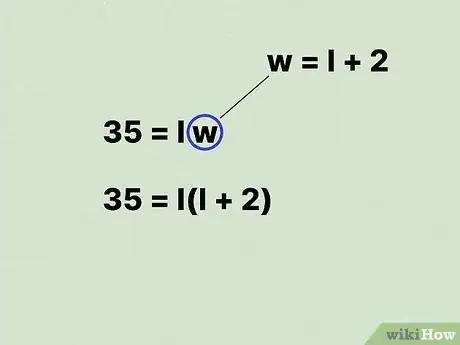
- Par exemple, si la longueur de votre rectangle est de 2 cm de plus que la largeur, écrivez la formule comme suit : $L=l+2$ .
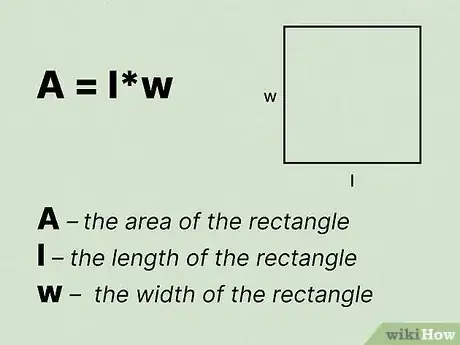
2
Écrivez la formule pour calculer l'aire. La formule est $A=Ll$ $A=Ll$ , où $A$ $A$ est l’aire du rectangle, $l$ $l$ représente la largeur, et $L$ $L$ représente la longueur ^{[12]
X
Source de recherche}.
- Vous pouvez utiliser cette méthode si vous connaissez le périmètre, mais en lieu et place, vous devez utiliser la formule du périmètre au lieu de celle de l’aire. La formule du périmètre d'un rectangle est la suivante : $P=2(L+l)$ , où $L$ est la longueur et $l$ la largeur ^{[13]
  X
  Source de recherche}.
3
Remplacez la valeur de l’aire dans la formule. Assurez-vous de remplacer la variable $A$ $A$ dans la formule.
- Par exemple, si l’aire du rectangle étudié est de 35 centimètres carrés, la formule sera la suivante : $35=Ll$ .
4
Remplacez la longueur ou la largeur dans la formule qui décrit la relation. Étant donné que la figure que vous étudiez est un rectangle, vous pouvez soit utiliser la variable $l$ $l$ ou $L$ $L$ .
- Par exemple, si vous avez trouvé que $L=l+2$ , remplacez cette relation par $L$ dans la formule de l'aire. Donc, vous obtiendrez
  $35=Ll$
  $35=l(l+2)$ .
5
Écrivez une équation du second degré. Pour ce faire, utilisez la propriété de distribution pour multiplier les termes entre parenthèses, ensuite supposez que l'équation est égale à zéro.
- Par exemple :
  $35=l(l+2)$
  $35=l^{2}+2l$
  $0=l^{2}+2l-35$ .
6
Factorisez votre équation du second degré. Pour plus de détails à ce sujet, consultez cet article.
- Par exemple, l'équation $0=l^{2}+2l-35$ peut être factorisée sous cette forme $0=(l+7)(l-5)$ .
7
Déterminez la valeur de la grandeur $l$ . Pour ce faire, supposez que chaque terme de l'équation est égal à zéro. Une équation du second degré admet deux racines également appelées solutions.
- Par exemple :
  $0=(l+7)$
  $-7=l$
  Et
  $0=(l-5)$
  $5=l$ .
  Dans ce cas, l’une des deux solutions est négative. Étant donné que l’on ne peut obtenir une grandeur négative, la largeur est forcément égale à 5 cm.
8
Remplacez la variable calculée dans la formule qui décrit la relation. Vous obtiendrez ainsi la valeur du deuxième côté du rectangle.
- Supposons que la largeur du rectangle est de 5 cm, et la relation entre les deux côtés est $L=l+2$ . À ce stade, vous pouvez remplacer la valeur 5 dans la formule pour obtenir ceci :
  $L=l+2$
  $L=5+2$
  $L=7$ .
9
Écrivez la formule du théorème de Pythagore. Cette formule est la suivante $a^{2}+b^{2}=c^{2}$ $a^{{2}}+b^{{2}}=c^{{2}}$ , où $a$ $a$ et $b$ $b$ représentent les côtés d’un triangle rectangle, et $c$ $c$ est l’hypoténuse de celui-ci ^{[14]
X
Source de recherche}.
- Vous pouvez utiliser le théorème de Pythagore, car la diagonale d'un rectangle divise celui-ci en deux triangles rectangles congruents ^{[15]
  X
  Source de recherche}. La longueur et la largeur représentent les côtés du triangle, alors que la diagonale représente l’hypoténuse.
10
Remplacez la largeur et la longueur dans la formule. Vous pouvez utiliser n’importe quelle valeur pour chaque variable.
- Considérons un rectangle dont la largeur et la longueur sont respectivement égales à 5 et 7 cm. La formule est la suivante : $5^{2}+7^{2}=c^{2}$ .
11
Mettez au carré ces deux variables et additionnez-les. N’oubliez pas qu’élever au carré un nombre revient à le multiplier par lui-même.
- Par exemple :
  $5^{2}+7^{2}=c^{2}$
  $25+49=c^{2}$
  $74=c^{2}$ .
12
Calculez la racine carrée de chaque terme de l'équation. La meilleure façon de le faire, c’est d'utiliser une calculatrice scientifique. Si vous n'en disposez pas, vous pouvez utiliser une calculatrice en ligne ^{[16]
X
Source de recherche}. De cette façon, vous allez obtenir la valeur de $c$ $c$ qui représente l'hypoténuse, ainsi que la diagonale.
- Par exemple,
  $74=c^{2}$
  ${\sqrt {74}}={\sqrt {c^{2}}}$
  $8,6024=c$
  Par conséquent, la diagonale d'un rectangle ayant une longueur de 2 cm de plus que la largeur et dont l’aire est de 35 cm mesure environ 8,6 cm.
Publicité