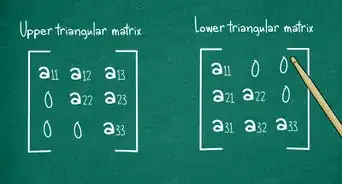Comment calculer le rayon d’un cercle

Le rayon d'un cercle correspond à la distance entre son centre et n'importe quel point de sa circonférence ^{[1]
X
Source de recherche}. La façon la plus facile de le calculer est de diviser le diamètre du cercle par deux. Si vous ne connaissez pas son diamètre, mais que vous disposez d'autres informations comme sa circonférence ( $C=2\pi r$ ) ou son aire ( $A=\pi r^{2}$ ), vous pouvez tout de même calculer le rayon en utilisant des formules mathématiques et en isolant la variable $r$ .

Méthode 1

Méthode 1 sur 4:

À partir de la circonférence

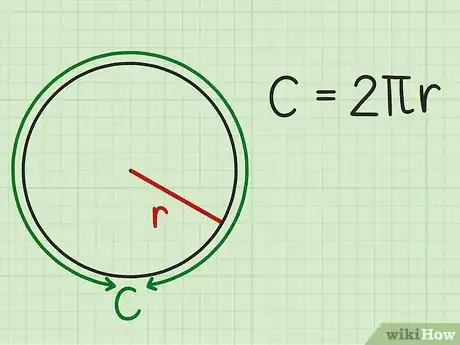
1
Écrivez la formule correspondante. Pour calculer le rayon d'un cercle à partir de sa circonférence, il faut employer la formule : $C=2\pi r$ $C=2\pi r$ , $C$ $C$ étant la circonférence (ou périmètre) et $r$ $r$ le rayon ^{[2]
X
Source de recherche}.
- Le symbole $\pi$ est un nombre spécial qui vaut environ 3,14. Vous pouvez utiliser le nombre approximatif 3,14 dans vos calculs ou bien la touche $\pi$ d'une calculatrice.
2
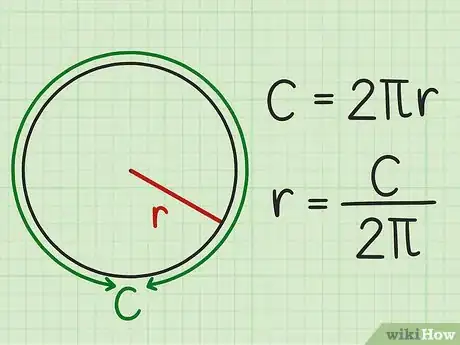
Isolez $r$ . Comme c'est le rayon que vous cherchez, vous devez arranger la formule afin d'isoler $r$ à gauche.

Exemple :
La formule de départ est : $C=2\pi r$ .

Vous divisez de chaque côté par $2\pi$ : ${\frac {C}{2\pi }}={\frac {2\pi r}{2\pi }}$ .

Vous simplifiez à droite : ${\frac {C}{2\pi }}={\frac {{\cancel {2\pi }}r}{\cancel {2\pi }}}$ .

Vous avez le rayon en fonction de la circonférence : $r={\frac {C}{2\pi }}$ .
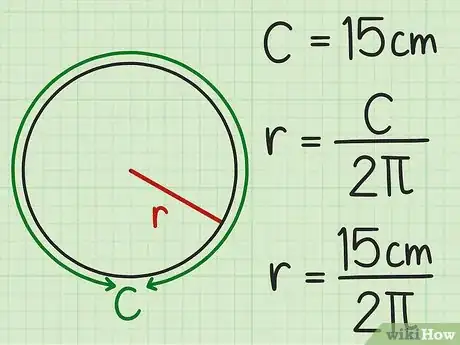
3
Faites l'application numérique. Lorsque l'on vous donne dans un exercice de mathématiques la circonférence d'un cercle et que l'on vous demande d'en calculer le rayon, utilisez la formule : $r={\frac {C}{2\pi }}$ , en remplaçant $C$ par la valeur donnée.

Exemple :
Pour un cercle d'une circonférence de 15 cm, la formule est : $r={\frac {15\ cm}{2\pi }}$ .
4
Faites le calcul. Sur votre calculatrice, utilisez la touche $\pi$ . Arrondissez le résultat obtenu à deux chiffres après la virgule. Si vous n'avez pas de calculatrice, faites le calcul à la main en utilisant 3,14 pour $\pi$ .

Exemple :
Reprenons notre cercle d'une circonférence de 15 cm :
$r={\frac {15}{2\pi }}={\frac {15}{2\times 3,14}}\approx {2,39\ cm}$ .

Publicité

Méthode 2

Méthode 2 sur 4:

À partir de l'aire

1
Écrivez la formule. Pour calculer le rayon d'un cercle à partir de son aire, il faut employer la formule $A=\pi r^{2}$ , $A$ étant l'aire du cercle et $r$ son rayon ^{[3]
X
Source de recherche}.
2
Isolez $r$ . Comme c'est le rayon que vous cherchez, vous devez arranger la formule afin d'isoler $r$ à gauche.

Exemple :
Dans la formule, divisez des deux côtés par $\pi$ :
${\frac {A}{\pi }}={\frac {\pi r^{2}}{\pi }}$ , soit ${\frac {A}{\pi }}={\frac {{\cancel {\pi }}r^{2}}{\cancel {\pi }}}$
${\frac {A}{\pi }}=r^{2}$
Prenez la racine carrée des deux côtés :
${\sqrt {\frac {A}{\pi }}}={\sqrt {r^{2}}}$
$r={\sqrt {\frac {A}{\pi }}}$ .
3
Faites l'application numérique. Lorsque l'on vous donne dans un exercice de mathématiques l'aire d'un cercle et que l'on vous demande d'en calculer le rayon, utilisez la formule : $r={\sqrt {\frac {A}{\pi }}}$ , en remplaçant $A$ par la valeur donnée.

Exemple :
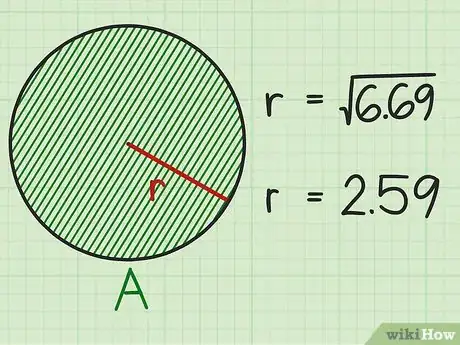
Prenons un cercle d'une aire de 21 cm² : $r={\sqrt {\frac {21}{\pi }}}$ .
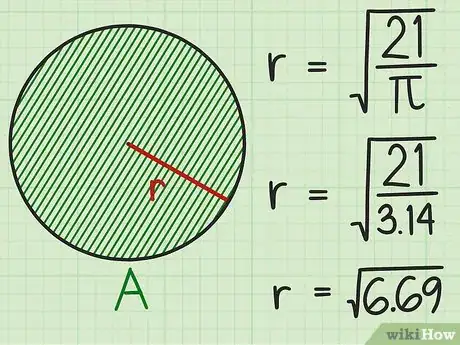
4
Divisez l'aire par $\pi$ . Calculez en priorité la quantité sous la racine, soit ${\frac {A}{\pi }}$ . Sur une calculatrice, vous utiliserez la touche $\pi$ , sinon, remplacez $\pi$ par sa valeur approximative de 3,14.

Exemple :
Par exemple, si vous utilisez 3,14 pour $\pi$ , vous obtenez :
$r={\sqrt {\frac {21}{3,14}}}$
$r={\sqrt {6,69}}$
Si vous pouvez entrer la formule dans votre calculatrice, vous obtenez un résultat plus précis.
5
Calculez la racine carrée. Calculez la racine carrée du résultat obtenu à l'étape précédente. Il vous faut une calculatrice, car vous obtiendrez un nombre décimal. Ce résultat est la longueur approximative du rayon.

Exemple :
Reprenons notre cercle d'une aire de 21 cm² :
$r={\sqrt {6,69\ cm^{2}}}\approx {2,59\ cm}$
Les aires sont toujours indiquées en unités carrées (en centimètres carrés, par exemple), tandis que les rayons sont toujours indiqués en unités simples (en centimètres, par exemple).

Publicité

Méthode 3

Méthode 3 sur 4:

À partir du diamètre

1
Repérez l'indication d'un diamètre. Dans un exercice, il est possible que l'on vous donne le diamètre d'un cercle et que l'on vous demande d'en calculer le rayon. Si ce n'était pas le cas, mais que l'on accompagne l'exercice d'une figure, vous devriez mesurer à la règle ce diamètre, soit la longueur entre 2 points du cercle en passant par le centre ^{[4]
X
Source de recherche}.
- Si vous ne savez pas exactement où se trouve le centre, positionnez la règle de façon approximative. Maintenez la graduation du 0 sur le bord du cercle et déplacez doucement l'autre extrémité de la règle sur le bord opposé. La mesure la plus grande que vous trouvez correspond au diamètre du cercle.
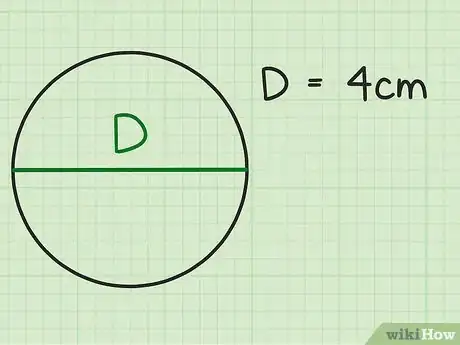
- Pour plus de clarté, nous allons prendre un cercle de 4 cm de diamètre.
2
Divisez le diamètre par deux. Par définition, la longueur du rayon d'un cercle est la moitié de celle de son diamètre ^{[5]
X
Source de recherche}.
- Si notre cercle a 4 cm de diamètre ( $d$ ), son rayon $r$ est de 2 cm
  ( $r={\frac {d}{2}}={\frac {4\ cm}{2}}=2\ cm$ ).
- La formule $r={\frac {d}{2}}$ découle de la formule $d=2r$ , le diamètre est égal à 2 fois le rayon. On passe de la seconde formule à la première en divisant des deux côtés par 2.
Publicité

Méthode 4

Méthode 4 sur 4:

À partir de l'aire et de l'angle d'un secteur circulaire

1
Écrivez la formule. Pour calculer le rayon d'un cercle à partir d'un secteur donné, vous devez employer la formule $A_{secteur}={\frac {\theta }{360}}\pi r^{2}$ , $A_{secteur}$ étant l'aire du secteur, $\theta$ (ou $\alpha$ ) l'angle central de ce secteur exprimé en degrés et $r$ le rayon du cercle ^{[6]
X
Source de recherche}.
2
Appliquez la formule à votre cercle. Si vous disposez de l'aire et de l'angle central d'un secteur du cercle, remplacez les lettres dans la formule par les valeurs correspondantes. Assurez-vous qu'il s'agit bien de l'aire de ce secteur et non du cercle entier. Remplacez $A_{secteur}$ par l'aire du secteur et $\theta$ par son angle.

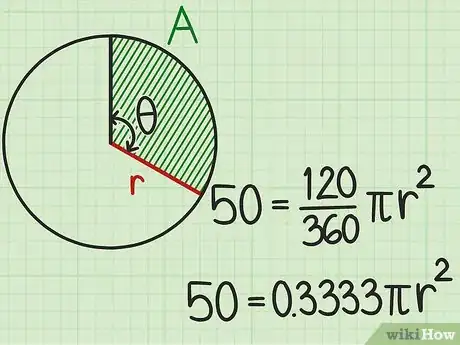
Exemple :
Dans un cercle, avec un secteur a une aire de 50 cm² et un angle de 120°, vous obtenez la formule suivante : $50={\frac {120}{360}}\pi r^{2}$ .
3
Divisez l'angle central par 360. Écrivez ce calcul sous forme de fraction simplifiée. Vous saurez ainsi quelle proportion du cercle entier le secteur représente.

Exemple :
L'angle de 120° est rapporté au cercle entier (360°) : ${\frac {120}{360}}={\frac {1}{3}}$ , ce qui signifie que le secteur représente un tiers du cercle. La formule se présente alors ainsi :
$50={\frac {1}{3}}\pi r^{2}$ .
4
Isolez $\pi r^{2}$ . Si vous avez une fraction dans votre formule, le plus simple pour simplifier est de faire le produit en croix.

Exemple :
Partez de : $50={\frac {1}{3}}\pi r^{2}$ .

Faites le produit en croix : $50\times 3=1\pi r^{2}$ .

Simplifiez : $\pi r^{2}=150$ .
5
Isolez $r$ . Divisez les deux côtés par $\pi$ pour isoler la variable $r$ . Pour obtenir un résultat aussi précis que possible, utilisez une calculatrice. Vous pouvez aussi remplacer $\pi$ par sa valeur approximative de 3,14.

Exemple :
Vous partez de : $\pi r^{2}=150$ .

Vous divisez de chaque côté par $\pi$ , puis simplifiez : ${\frac {{\cancel {\pi }}r^{2}}{\cancel {\pi }}}={\frac {150}{\pi }}$ .

Vous obtenez : $r^{2}\approx {47,7}$ .
6
Calculez $r$ . Calculez la racine carrée des deux côtés de l'équation pour trouver le rayon du cercle.

Exemple :
Vous partez de : $r^{2}=47,7$ .
Prenez la racine carrée des deux termes : ${\sqrt {r^{2}}}={\sqrt {47,7}}$ .
Faites le calcul : $r\approx {6,91\ cm}$ .
Le cercle a donc un rayon d'environ 6,91 cm.

Publicité

Conseils

Le nombre $\pi$ est fondateur du cercle dans la mesure où sa valeur est, quelle que soit la taille du cercle, le rapport de la circonférence $C$ au diamètre $d$ : $\pi ={\frac {C}{d}}$ . Cela marche avec tous les cercles !