Comment calculer la surface d’une figure géométrique

Informations concernant l'auteur.e

Qui dit aire, dit espace à deux dimensions. Parfois, il suffit de multiplier deux nombres pour obtenir une aire, parfois il y faut des calculs un peu plus complexes. Il est possible de calculer l'aire d'un quadrilatère, d'un triangle, d'un cercle, d'un prisme (aire totale), d'un cylindre (aire totale), même sous une courbe. En fait, pour les aires complexes, il est possible de les décomposer en somme d'aires de figures simples.

Méthode 1

Méthode 1 sur 10:

Calculer l'aire d'un rectangle

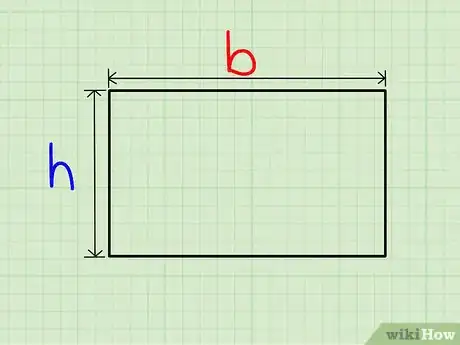
1
Déterminez la longueur et la largeur du rectangle. Ces deux côtés sont consécutifs, car un rectangle est constitué de quatre côtés, égaux deux à deux et opposés. La longueur est par convention notée $L$ , tandis que la largeur est notée $l$ , la première a une longueur supérieure à la seconde.
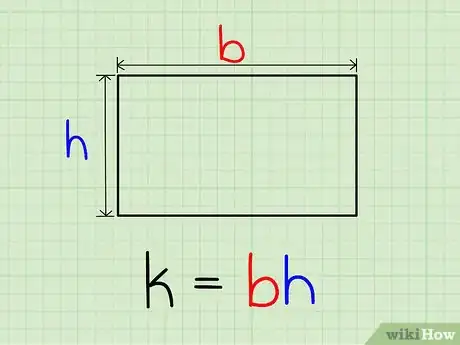
2
Multipliez la longueur d'un rectangle par la largeur. C'est ainsi que vous obtiendrez son aire. Si $A$ est l'aire, alors sa formule est : $A=L\times l$ . c'est simple, puisqu'il n'y a que deux nombres à multiplier.

Publicité

Méthode 2

Méthode 2 sur 10:

Calculer l'aire d'un carré

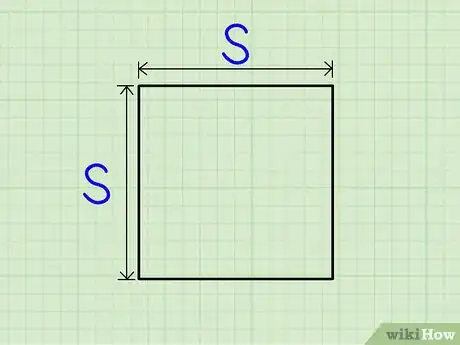
1
Déterminez la longueur d'un des côtés du carré. Par définition, un carré est une figure ayant 4 côtés (notés $a$ ) et 4 angles droits (90°). Pour l'aire, vous avez besoin de la longueur d'un seul côté.
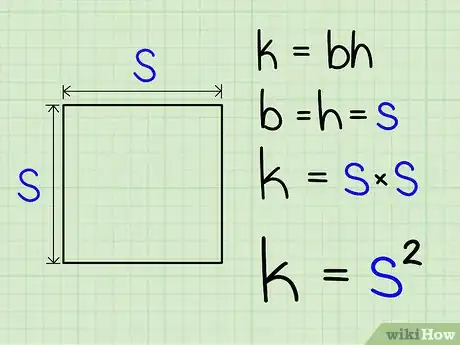
2
Élevez cette valeur au carré. Vous obtenez votre aire.
- En fait, l'aire du carré est la même que celle du rectangle, étant donné qu'un carré n'est jamais qu'un rectangle ayant des côtés égaux. La formule de l'aire ( $A$ ) du carré est : $A=a\times a=a^{2}$ .
Publicité

Méthode 3

Méthode 3 sur 10:

Calculer l'aire d'un parallélogramme

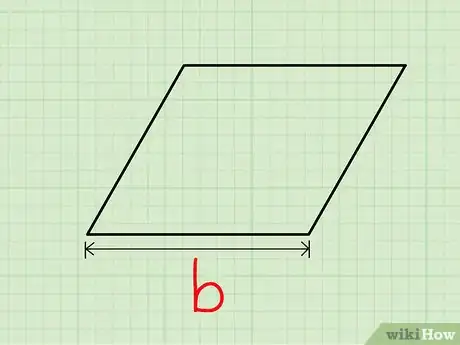
1
Choisissez un des côtés comme base du parallélogramme. Mesurez la longueur de cette base ( $b$ ).
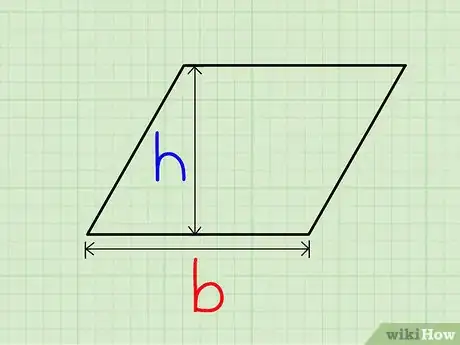
2
Tracez la hauteur ( $h$ ). C'est une ligne qui part à angle droit (90°) de la base choisie et se termine sur le côté opposé (aussi appelé base). Cette ligne doit être perpendiculaire aux deux bases.
- Si le côté opposé à la base n'est pas assez long pour tracer la hauteur, prolongez en pointillés la base opposée du côté qui vous arrange.
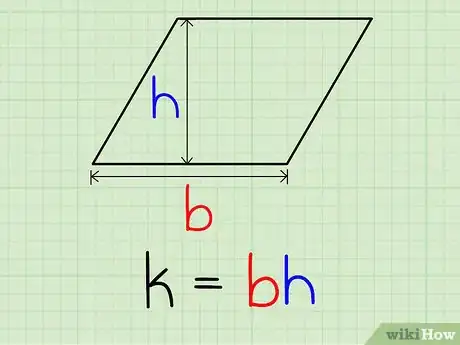
3
Calculez l'aire du parallélogramme. La formule de calcul est la suivante :
$A=b\times h$ .

Publicité

Méthode 4

Méthode 4 sur 10:

Calculer l'aire d'un trapèze

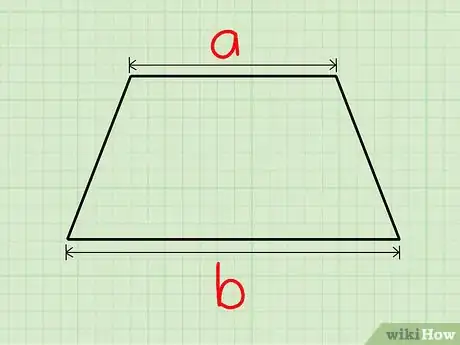
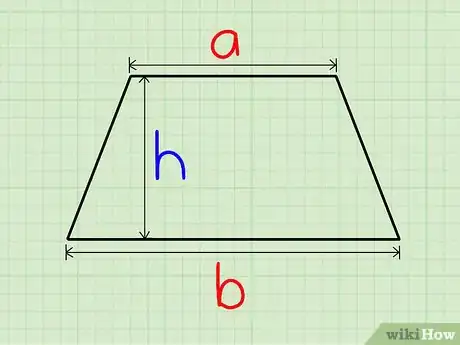
1
Déterminez la longueur des bases. Sont appelés bases dans un trapèze les deux segments parallèles. La plus grande base est notée $B$ , la petite $b$ .
2
Déterminez la hauteur. Tracez une ligne qui va d'une base à l'autre, perpendiculaire aux deux bases : c'est la hauteur ( $h$ ). Mesurez-la.
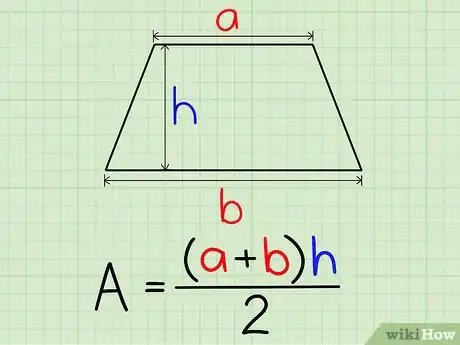
3
Calculez l'aire $A$ du trapèze. La formule de calcul est la suivante :
$A={\frac {(B+b)h}{2}}$ $A={\frac {(B+b)h}{2}}$ .
- Pour plus de détails, consultez cet article.
Publicité

Méthode 5

Méthode 5 sur 10:

Calculer l'aire d'un triangle

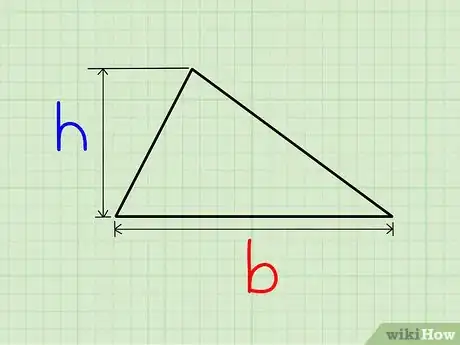
1
Déterminez la base et la hauteur de votre triangle. Mesurez un des côtés du triangle (celui qui est horizontal en général), ce sera la base. Mesurez aussi la hauteur associée à cette base. C'est le segment de droite qui part à l'angle droit (90°) de la base et aboutit au sommet opposé.
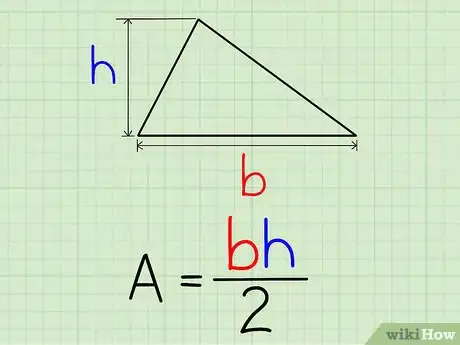
2
Calculez l'aire du triangle. Soit $A$ l'aire du triangle, la formule de calcul est la suivante : $A={\frac {1}{2}}bh={\frac {bh}{2}}$ .

Publicité

Méthode 6

Méthode 6 sur 10:

Calculer l'aire d'un polygone régulier

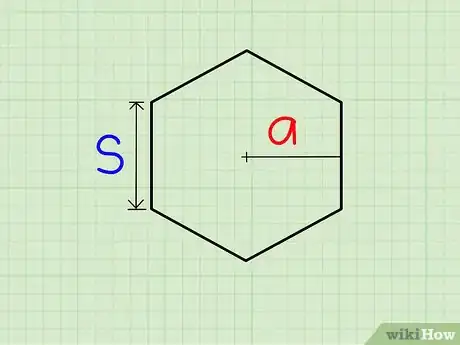
1
Déterminez deux longueurs. Pour ce calcul de l'aire d'un polygone régulier, vous devez connaitre la longueur d'un des côtés ( $c$ ) et celle de l'apothème ( $a$ ). Cette dernière est la distance du centre du polygone au centre d'un quelconque côté.
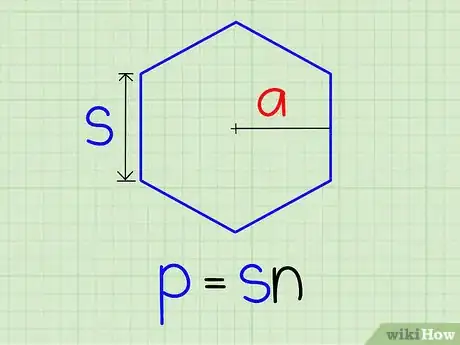
2
Calculez le périmètre ( $P$ ) du polygone. Multipliez la longueur ( $c$ ) d'un côté par le nombre ( $n$ ) de côtés : $P=c\times n$ .
3
Calculez l'aire d'un polygone régulier. La formule de calcul est la suivante :
$A={\frac {1}{2}}cp$ .

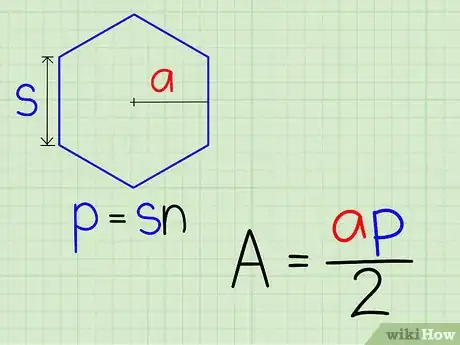
Publicité

Méthode 7

Méthode 7 sur 10:

Calculer l'aire d'un cercle

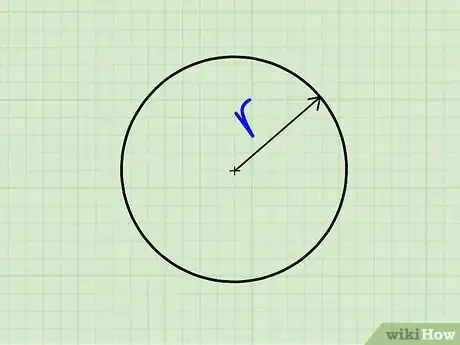
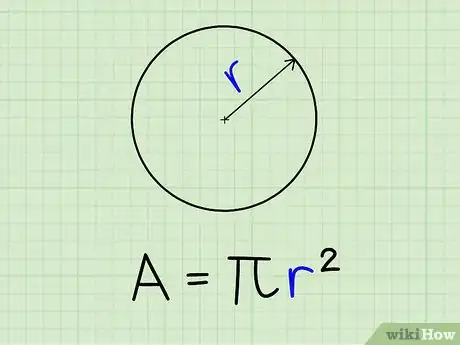
1
Déterminez le rayon du cercle ( $r$ ). C'est le segment de droite qui part du centre du cercle et rejoint n'importe quel point du périmètre.
2
Calculez l'aire d'un cercle. Avec comme seule donnée le rayon du cercle, vous pouvez calculer son aire avec la formule suivante : $A=\pi r^{2}$ $A=\pi r^{2}$ .
- Pour plus de détails, consultez cet article.
Publicité

Méthode 8

Méthode 8 sur 10:

Calculer l'aire totale d'une pyramide

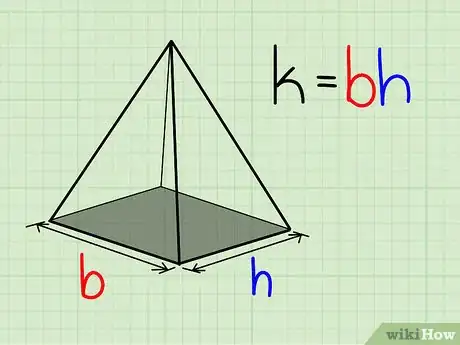
1
Déterminez l'aire de la face de base. Cette base est soit carrée soit rectangulaire, et son aire s'obtient avec la formule vue plus haut : $A=L\times l$ ,
$L$ étant la longueur et $l$ la largeur.
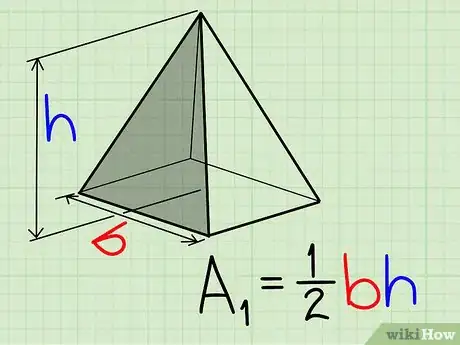
2
Calculez l'aire de chacun des côtés triangulaires. Utilisez la formule vue plus haut, à savoir : $A={\frac {1}{2}}bh={\frac {bh}{2}}$ .
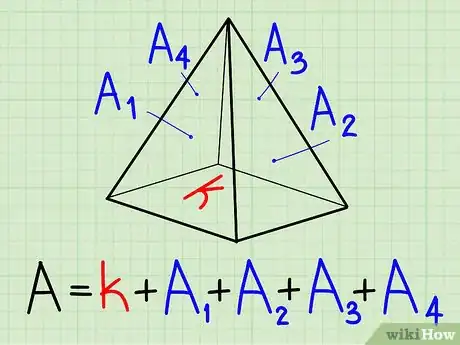
3
Faites la somme de toutes ces aires. Si les faces sont identiques, toutes ou deux par deux, il est inutile de faire deux fois les calculs. Ainsi, sur le dessin, on voit que les faces A1 et A3 sont identiques, tout comme les faces A2 et A4.

Publicité

Méthode 9

Méthode 9 sur 10:

Calculer l'aire totale d'un cylindre

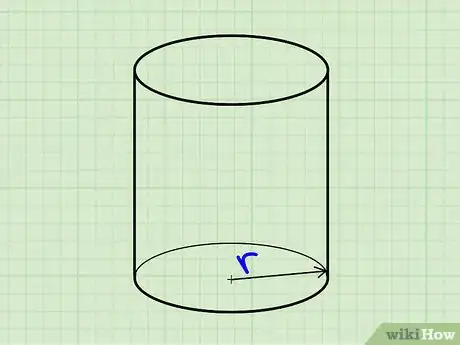
1
Déterminez le rayon d'un des cercles de base.
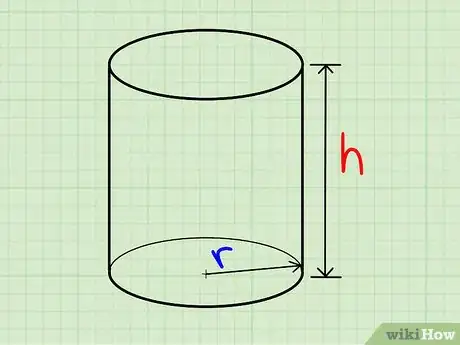
2
Déterminez la hauteur du cylindre.
3
Déterminez l'aire de la base circulaire. La formule est celle du cercle, soit :
$A=\pi r^{2}$ .
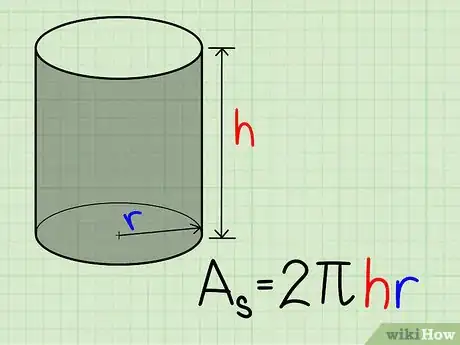
4
Déterminez l'aire de la face latérale. C'est en fait un rectangle qui a comme longueur la hauteur et comme largeur le périmètre de la base. Le périmètre ( $P$ ) du cercle est : $P=2\pi r$ , donc l'aire ( $A$ ) de la face latérale est : $A=2\pi rh$ .
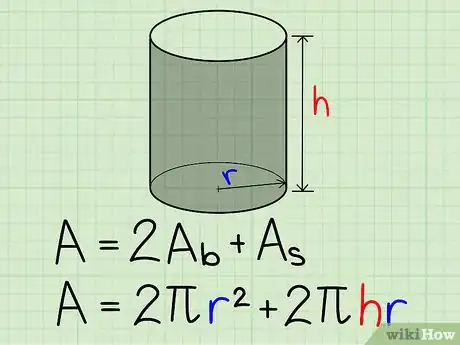
5
Faites la somme de toutes ces aires. L'aire totale est la somme des aires des 2 faces circulaires ( $A_{c}$ $A_{c}$ ) et une face latérale ( $A_{l}$ $A_{l}$ ) : il faut donc les additionner :
$A_{totale}=A_{c}+A_{l}=2(\pi r^{2})+2\pi hr$ $A_{totale}=A_{c}+A_{l}=2(\pi r^{2})+2\pi hr$ .
- Pour plus de détails, consultez cet excellent article.
Publicité

Méthode 10

Méthode 10 sur 10:

Calculer l'aire sous une courbe

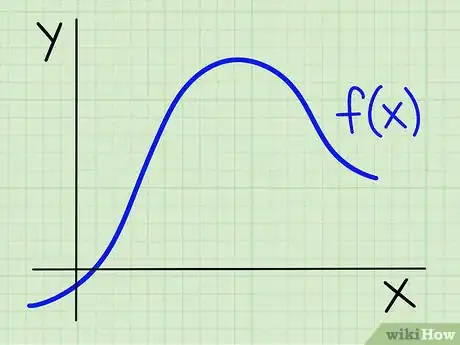
Supposons que vous vouliez déterminer l'aire qui se trouve entre une courbe (celle de la fonction f(x) sur un intervalle [a, b]) et l'axe des abscisses (axe des x). Cette partie ne peut être réalisée que par celles et ceux qui savent analyser une fonction, et ont déjà des notions sur les intégrales.

1
Analysez $f(x)$ . Pour pouvoir déterminer une aire sous la courbe, la fonction doit être continue et positive sur l'intervalle considéré.
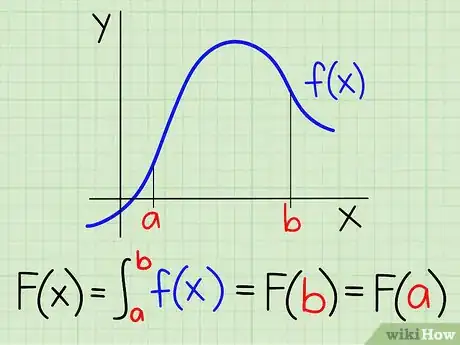
2
Prenez l'intégrale de $f(x)$ sur [a, b]. L'aire $A$ comprise sous la courbe, au-dessus de l'axe des abscisses et entre les droites d'équation $x=a$ et $x=b$ , est : $A=\int _{a}^{b}f(x)dx=F(b)-F(a)$ , $F$ étant une des primitives de $f$ .
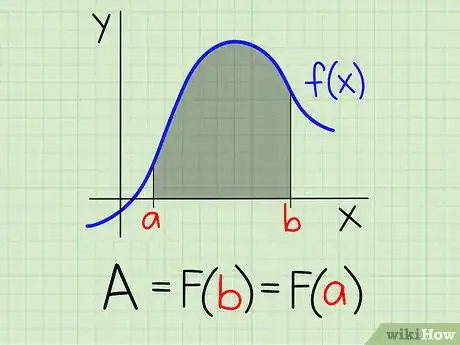
3
Calculez l'aire sous la courbe. Trouvez une primitive ( $F$ ) de votre fonction, celle que vous voulez, calculez $F(b)-F(a)$ et vous aurez votre aire sous la courbe entre $a$ et $b$ . Le résultat est obtenu en unités d'aire, définies par $OI$ et $OJ$ du repère utilisé.

Publicité