Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 101 950 fois.
Le rapport de la masse d’un objet à son volume est sa masse volumique. C’est une grandeur physique fréquemment utilisée en physique, en chimie, en géologie… La connaissant, vous saurez si votre objet d’étude coule ou non (flottabilité) lorsqu’il est plongé dans l’eau, dont la masse volumique est de 1 gramme par centimètre cube (g/cm3).
Étapes
Préparer le calcul d’une masse volumique
-
1Trouvez la tare de votre contenant. Pour évaluer la masse d’un liquide, vous devez connaitre la masse du récipient qui le contient : c’est la tare. Pesez le récipient à vide, puis rempli de votre substance et faites différence entre les deux pour avoir la masse de la substance étudiée [1] .
- Placez votre récipient sur la balance, laissez cette dernière se stabiliser, puis notez sur votre feuille sa masse à vide.
- Certaines balances électroniques sont équipées d’une fonction « tare ». Posez le récipient vide sur le plateau, appuyez sur le bouton de calibrage et l’appareil se remet à 0. Si vous versez un liquide, vous aurez directement sa masse.
-
2Trouvez la masse de votre substance. Avec ou sans récipient, mesurez la masse de votre substance en la posant sur le plateau de la balance. Si la balance est calibrée, vous avez directement sa masse, sinon vous ferez la différence avec la tare trouvée [2] .
-
3Convertissez la masse trouvée en kilogrammes. L’unité de la masse volumique dans le Système international d’unités est le kilogramme par mètre cube (kg/m3), mais rien ne vous empêche dans la vie quotidienne d’utiliser le gramme par centimètre cube. Si vous avez une masse en grammes, convertissez-la en kilogrammes et les centimètres cubes en mètres cubes.
- Pour passer des grammes aux kilogrammes, divisez par 1 000 (100 g = 0,1 kg) et pour passer des centimètres cubes aux mètres cubes, divisez par un million (10 000 cm3 = 0,01 m3).
- Pour passer des grammes par centimètre cube aux kilogrammes par mètre cube, il suffit de multiplier par 1 000 (10 g/cm3 = 10 000 kg/m3).
-
4Déterminez le volume d’un objet géométrique. Si vous avez une substance, liquide par exemple, qui remplit complètement un volume régulier (cube, parallélépipède), mesurez la longueur, la largeur et la hauteur du contenant, multipliez-les et vous aurez votre volume [3] .
-
5Déterminez le volume d’un objet irrégulier. Pour un liquide, vous pouvez, par exemple, utiliser un récipient gradué (bécher, éprouvette). Pour un solide ayant une forme géométrique, vous utiliserez la formule adaptée, sinon vous utiliserez la méthode du déversement.
- 1 millilitre est équivalent à 1 centimètre cube. À condition de retenir la conversion, le passage d’une unité à l’autre est simple !
- Il existe une formule de calcul du volume par forme géométrique, une pour le parallélépipède, une pour le cylindre, une pour la pyramide, etc.
- Si votre objet est solide et irrégulier (par exemple, un galet), il n’existe pas de formule toute faite pour trouver son volume. Prenez un récipient gradué ou un vase à déversement rempli d’eau. Vous notez le volume d’eau au départ, vous y plongez votre objet et vous faites la différence entre les deux volumes : c’est le volume de l’objet concerné [4] .
Publicité
Savoir utiliser la formule de la masse volumique
-
1Divisez la masse de l’objet par son volume. Selon votre inclination, calculez à la main ou avec une calculatrice, le rapport, comprenez la division, de la masse de votre objet (en grammes) à son volume (en cm3). Un objet d’une masse de 20 g qui occuperait un volume de 5 cm3 aurait une masse volumique de 4 g/cm3 [5] .
-
2Arrondissez éventuellement la masse volumique. Comme vous faites une division, il est fort probable que vous obteniez un résultat décimal. Tout dépend alors du contexte de votre expérience. Si c’est un exercice scolaire, votre professeur vous indiquera le degré de précision qu’il veut (1, 2, 3… décimales). Si vous voulez déterminer, par exemple, le poids d’une construction en béton à venir, peut-être qu’une seule décimale suffira.
- Faites attention, car cet arrondissement est moins innocent qu’il y parait. Dans une situation de la vie courante, le choix d’une ou deux décimales sur des volumes importants peut donner des différences de masse très importantes.
- Le plus souvent, on arrondit une masse volumique à deux ou trois décimales. Admettons que votre calculatrice ait affiché une masse volumique brute de 32,714907 g/cm3, vous pourrez l’arrondir à 32,71 ou 32,715.
-
3Passez de la masse volumique à la densité. Cette dernière s’obtient en faisant le rapport de la masse volumique d’un objet à la masse volumique de l’eau (1 g/cm3). Si la densité de votre objet est supérieure à 1, il coulera dans l’eau, sinon il flottera.
- Cette densité est intéressante pour déterminer la miscibilité ou non de deux liquides. Ainsi, la plupart des huiles ont une densité inférieure à 1, ce qui explique qu’elles flottent quand on les déverse sur de l’eau.
- La densité relative est une autre grandeur qui se calcule à partir de masses volumiques. Elle se calcule entre la masse volumique d’un corps et celle d’un autre corps de référence, souvent l’eau ou l’air, mais non systématiquement. Lors du calcul de cette grandeur, les unités s’annulent, ce qui fait qu’une densité s’exprime sans unité aucune. Cette notion de densité relative est fréquemment utilisée en chimie, quand sont concernés des composés avec des concentrations différentes [6] .
Publicité
Éléments nécessaires
- Une balance ou un peson
- Une règle ou tout autre instrument de mesure de longueur
- Une calculatrice
- Un récipient gradué (pour mesurer le volume d’un liquide ou d’un gaz)
Références
- ↑ https://www.grc.nasa.gov/WWW/K-12/airplane/fluden.html
- ↑ https://sciencing.com/calculate-mass-weight-6399639.html
- ↑ https://serc.carleton.edu/mathyouneed/density/index.html
- ↑ https://sciencing.com/do-volume-object-6199021.html
- ↑ https://serc.carleton.edu/mathyouneed/density/index.html
- ↑ https://serc.carleton.edu/mathyouneed/density/index.html







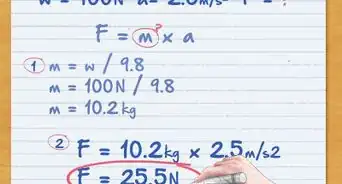











L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 101 950 fois.