إحصاء الجسيمات

في الميكانيك الكلاسيكي فإن كل الجسيمات سواءً كانت أولية أم مركبة، أو الذرات أو الجزيئات أو الإلكترونات فإنها تعد مميزة بحد ذاتها، أي أنه يمكن وسم إحداها وتتبعها ضمن نظام ما. بناءً على ذلك فإن تغيير موقع الجسيمات في نظام ما سيؤدي إلى حدوث تشكيل مختلف تماماً للنظام ككل. بالإضافة إلى ذلك فإنه لا يوجد تقييد على وضع جسيم واحد أو أكثر في أي وضع أو حالة افتراضية متاحة للنظام. يدعى الإحصاء الكلاسيكي للجسيمات باسم إحصاء ماكسويل-بولتزمان.

حسابات إحصاء الكم.

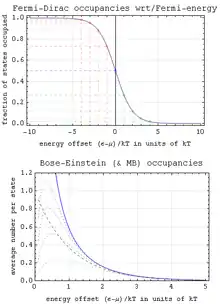
إن الميزة الأساسية لميكانيك الكم عن الميكانيك الكلاسيكي أن الجسيمات في إحصاء الكم هي جسيمات متماثلة لا تميز عن بعضها البعض. مما يعني أن تبديل أي جسيم في المجموعة الإحصائية المكونة من جسيمات متماثلة لا يؤدي إلى حدوث تشكيل جديد للنظام. يمكن التعبير عن ذلك بلغة ميكانيكا الكم أن الدالة الموجية للنظام غير متغيرة وذك في حال حدوث تغير في الجسيمات المكونة للنظام.

من الأمور المهمة التي ينبغي معرفتها في إحصاء الكم هو مقدار درجة الحرية للجسيمات. إن كل الجسيمات لها ثلاث درجات حرية في الحركة الانزلاقية بالإضافة إلى درجة حرية متقطعة (منفصلة) وهي اللف المغزلي، بالإضافة إلى كون جميع الجسيمات مؤلفة من جسيمات دون ذرية. بناء على ذلك، فإنه كلما كانت الجسيمات أكثر تعقيداً كلما كان أثر إحصاء الكم أقل. لذلك فإن استخدام وسائل إحصاء الكم يعد مفيداً في حالات مادة مثل الهيليوم السائل أو غاز الأمونيا، ولكنه لا يفيد في حالة جسيمات معقدة مثل الجزيئات الضخمة.

هناك نوعين من إحصاء الكم وذلك اعتماداً على تناظر النظام وهما إحصاء بوز-أينشتاين وإحصاء فيرمي ديراك، وذلك أن مبرهنة إحصاء اللف المغزلي تربط نوعين من زمرة التبديلات مع نوعين من زمرة اللف المغزلي.

• بوابة الفيزياء