انسحاب (هندسة)
في الفضاء الإقليدي، الانسحاب أو الإزاحة أو الانزلاق (بالإنجليزية: Translation) هو تحريك كل النقاط المتواجدة في الفضاء لمسافة محددة وبنفس الاتجاه.[1][2][3] وتعد إحدى الزمر الاقليدية الصارمة الحركة. والنوعان الصارما الحركة هما الدوران والانعكاس. كما يمكن وصف الانزلاق بإضافة متجه شعاعي ذي قيمة محددة لكل النقاط في الفضاء أو نقل مركز الإحداثيات.

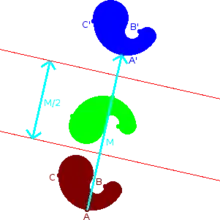
إن معامل الأنزلاق هو معامل حيث .
إذا كان v متجها شعاعيا ثابتا، فإن الانزلاق Tv يعمل مثل Tv(p) = p + v.
إذا اعتُبر أن T هي انزلاق، فان صورة (image) المجموعة الجزئية A بتأثير الدالة T هي «انزلاق» A بـ Tv. والتي تكتب بالعادة كـ A + v.
التشكيل المصفوفي
بما أن الانزلاق هو تحويل أفيني وليس تحويل خطي، فبالعادة تستعمل الإحداثيات المتجانسة لتمثيل معامل التحويل كمصفوفة رياضية وبالتالي تحويلها لعملية خطية. لذلك، نكتب التوجه الشعاعي الثلاثي الأبعاج w تساوي (wx, wy, wz) مستعملين 4 إحداثيات متجانسة w تساوي (wx, wy, wz, 1) . ولنقل مجسم بموجه شعاعي v يضرب كل متجه شعاعي متجانس p بالمصفوفة التالية:
وكما يظهر في النتيجة التالية، حاصل الضرب يكون كالمتوقع:
ويمكن الحصول على عكس مصفوفة الانزلاق بعكس الموجه الشعاعي:
وبنف المعيار، فان حاصل ضرب المصفوفات الانزلاقية هم مجموع المتجهات الشعاعية:
وبما أن جمع المتجهات الشعاعية هي عملية تبديلية (commutative)، لذلك عملية ضرب المصفوفات الانزلاقية هي عملية تبديلية أيضا، بخلاف عملية ضرب مصفوفات عشوائية.
مراجع
راجع: نقل (هندسة رياضية)، انعكاس انزلاقي، مجموعة افريزية (هندسة)، مجموعة ورق الجدران (هندسة)
- "معلومات عن انزلاق (هندسة) على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 30 مايو 2019.
- "معلومات عن انزلاق (هندسة) على موقع britannica.com"، britannica.com، مؤرشف من الأصل في 2 أبريل 2017.
- "معلومات عن انزلاق (هندسة) على موقع psh.techlib.cz"، psh.techlib.cz، مؤرشف من الأصل في 13 ديسمبر 2019.
- بوابة رياضيات
- بوابة هندسة رياضية
- بوابة الرسوميات الحاسوبية