شبه منحرف

لتكن K مساحة شبه منحرف كيفي

K بدلالة القاعدتين الكبرى والصغرى والارتفاع تكون: ${\displaystyle K={\frac {a+b}{2}}\cdot h}$

K بدلالة الأضلاع الأربعة تكون:${\displaystyle K={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}}}$

حيث أن: ${\displaystyle s={\tfrac {1}{2}}(a+b+c+d)}$

K حسب علاقة بريتشنايدر:${\displaystyle K={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{(2(b-a))^{2}}}-\left({\frac {b^{2}+d^{2}-a^{2}-c^{2}}{4}}\right)^{2}}}}$

ارتفاع شبه المنحرف بدلالة الأضلاع الأربعة يكون حسب العلاقة التالية:

${\displaystyle h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}}$

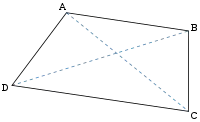
القاعدتان الكبرى والصغرى لشبه منحرف كيفي بدلالة القطرين والضلعين الجانبيين حسب علاقة بن عيشة جمال الدين:

${\displaystyle b={\sqrt {\frac {(c^{2}-p^{2})^{2}-(d^{2}-q^{2})^{2}}{2(c^{2}+p^{2})-2(d^{2}+q^{2})}}}}$

${\displaystyle a={\sqrt {\frac {(d^{2}-p^{2})^{2}-(c^{2}-q^{2})^{2}}{2(d^{2}+p^{2})-2(c^{2}+q^{2})}}}}$

حيث أن AC=p، BD=q، AD=c و BC=d مع p لايساوي q.

يمكن استعمال علاقة جمال في اثبات توازي مستقيمين، حيث بالنسبة للشكل الذي لدينا: إذا كان 0<b² فإن a و b متوازيان، وإذا كان b²<0 فإن a و b غير متوازيين.

يمكن حساب قطري شبه المنحرف انطلاقا من الأطوال الأربعة باستخدام العلاقة التالية:

${\displaystyle p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}}}$

${\displaystyle q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}}}$

مع p لايساوي q. الا في حالة ان يكون شبه المنحرف متطابق الساقين

• شبه منحرف متساوي الساقين
• متوازي الأضلاع

• إيريك ويستاين، شبه منحرف، ماثوورلد Mathworld (باللغة الإنكليزية).

• بوابة رياضيات
• بوابة هندسة رياضية

جزء من سلسلة مقالات حول
الهندسة الرياضية
الخطوط العريضة [الإنجليزية] التاريخ
الفروع إقليدية لاإقليدية إهليلجية كروية زائدية لا أرخميدية [الإنجليزية] إسقاطية نسبية تركيبية تحليلية جبرية حسابية ديوفانية [الإنجليزية] تفاضلية ريمانية هندسة تماسكية عقدية منتهية متقطعة رياضية رقمية محدبة رياضية حاسوبية وقعية [الإنجليزية]
المبادئ الخواص بعد الإنشاء بالمسطرة والفرجار زاوية منحنى ضلع قطري تعامد رياضي (تعامد هندسي) تواز رأس تطابق تشابه تناظر
صفري الأبعاد نقطة
وحيد البعد الطول مستقيم قطعة مستقيمة
المُسطَّحات مستو مساحة مضلع المثلثات مثلث الارتفاع الوتر مبرهنة فيثاغورس متوازيات الأضلاع متوازي أضلاع مربع مستطيل معين شبه معين رباعيات الأضلاع رباعي أضلاع شبه منحرف طائرة ورقية المنحنيات دائرة القطر المحيط المساحة قطع ناقص
المُجسَّمات حجم مكعب متوازي مستطيلات أسطوانة هرم كرة
ما فوق البعد الثالث مكعب رباعي الأبعاد كرة نونية الأبعاد
علماء الهندسة
وفق الاسم أيدا أريابهاتا أحمس [الإنجليزية] ابن الهيثم أبلونيوس أرخميدس عطية بولياي براهماغوبتا كارتن كوكستر ديكارت إقليدس أويلر غاوس غروموف هيلبرت جيهاديفا [الإنجليزية] كاتيايانا الخيَّام كلاين لوباتشيفسكي مانافا [الإنجليزية] مينكوفسكي مينغاتو [الإنجليزية] باسكال فيثاغورس باراميشفارا [الإنجليزية] بوانكاريه برنارد ريمان سكابي [الإنجليزية] السجزي الطوسي فيبلين [الإنجليزية] فيراسينا [الإنجليزية] يانغ هوي [الإنجليزية] ابن الياسمين زانج قائمة علماء الهندسة
وفق الحقبة قبل الميلاد أحمس [الإنجليزية] مانافا [الإنجليزية] فيثاغورس إقليدس أرخميدس أبلونيوس 1–1400م زانج كاتيايانا أريابهاتا براهماغوبتا فيراسينا [الإنجليزية] ابن الهيثم السجزي الخيَّام ابن الياسمين الطوسي يانغ هوي [الإنجليزية] باراميشفارا [الإنجليزية] 1400–1700م جيهاديفا [الإنجليزية] ديكارت باسكال مينغاتو [الإنجليزية] أويلر سكابي [الإنجليزية] أيدا 1700–1900م غاوس لوباتشيفسكي بولياي برنارد ريمان كلاين بوانكاريه هيلبرت مينكوفسكي كارتن فيبلين [الإنجليزية] كوكستر معاصرون عطية غروموف
بوابة هندسة رياضية