هندسة حسابية
في الرياضيات، تعد الهندسة الحسابية هي تطبيق تقنيات من الهندسة الجبرية إلى المشاكل في نظرية الاعداد الصحيحة.[1] تتمحور الهندسة الحسابية حول هندسة الديوفانتين، دراسة النقاط المنطقية للاصناف الجبرية.[2][3]
| جزء من سلسلة مقالات حول |
| الهندسة الرياضية |
|---|
 |
|
| علماء الهندسة |
| بوابة هندسة رياضية |
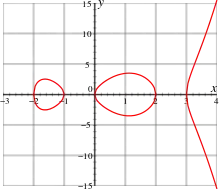
يمكن تعريف الهندسة الحسابية على أنها دراسة مخططات من النوع المحدود عبر حلقة الأعداد الصحيحة.[4]
نظرة عامة
الأشياء الكلاسيكية ذات الأهمية في الهندسة الحسابية هي نقاط عقلانية من حلول نظام متعدد الحدود من المعادلات على حقول الأرقام أو الحقول المحدودة أو الحقول الوظيفية. أي الحقول غير المغلقة جبريا باستثناء الأعداد أو الأرقام الصحيحة. يمكن أن تكون النقاط المنطقية مباشرة تتميز بوظائف الارتفاع تقيس التعقيد الجمالي لهيكل الأصناف الجبرية المحددة.[5]
هيكل الأصناف الجبرية المحددة على غير الحقول المغلقة جبريا منطقة مركزية لاهتمام الذي نشأ مع التطور التجريدي الحديث لهندسة الجبرية. عبر مدى مجالات محدودة، علم التعايش الجماعي يوفر الثوابت الطوبولوجية المرتبطة بالجبر. نظرية هودج تعطي أدوات لفحص متى الخصائص المشتركة للأصناف على مدى المجمع التي تلك الموجودة فوق الحقول.
التاريخ
القرن التاسع عشر: الهندسة الحسابية المبكرة
في أوئل القرن التاسع عشر، لاحظ كارل فريدريش جاوس ذلك حلول الأعداد الصحيحة غير الصفرية لكثير حدود متجانسة في أوئل القرن توجد معاملات ذات المعاملات العقلانية غير الصفرية.[6]
في خمسينات القرن التاسع عشر، صاغ ليوبولد نظرية، أي نظرية ويبر، قدمت نظرية القواسم وصنع نظرية الأعداد العديدة من الروابط الأخرى بين نظرية الأعداد والجبر. ثم تخمن له تعميم (أعز حلم الشباب) تم وضعه لاحقا إلى الامام من قبل هيلبرت في شكل معدل باعتباره مشكلته الثانية عشر وهو التعميم حاصل من الحل التي تحدد هدفا لجعل نظرية الأعداد الصحيحة.[7]
من أوائل القرن العشرين إلى منتصفه: التطورات الجبرية وتخمينات ويل
في أواخر العشرينات من القرن الماضي، أظهر أندريه ويل بعمق الجرية ونظرية الروابط بين الهندسة الجبرية ونظرية الأعداد مع عمله الدكتوراه الذي أدى إلى نظرية أن مجموعة النقاط المنطقية لأبليان متنوعة هي مجموعة أبليان ولدت بشكل نهائي.[8]
تطورت الأسس الحديثة للهندسة الجبرية على أساس الجبر التبادلي المعاصر، بما في ذلك نظرية التقييم ونظرية المثل العليا لأوسكار زاريسكي وآخرون في الثلاثينات والأربيعنيات.[9]
في عام 1949، طرح أندريه ويل تخمينات ويل التاريخية حول وظائف زيتا المحلية لأصناف الجبرية علة المنتهية الجبرية ونظرية تستخدم نظرية الحقول.[10] قدمت هذه التخمينات إطار بين الهندسة الجبرية ونظرية الأعداد التي دفعت في الخمسينات الكسندر جروتينديك لإعادة صياغة الأسس زيتا المحلية من تخمينات ويل إثبات من نظرية الحزم (مع جان بيير سير) و نظرية المخطط لاحقا، في الخمسينات والستينات. برنارد دورك أثبت أحد عقلانية المحلي. تخمينات في عام 1960.[11] طور نظرية لأثبات اثنين من تخمينات بقلم مايكل أرتين وجان لويس فيريدير في 1965.[12][13] اخ تخمينات ويل (تناضرية لفرضية ريمان) أخيرا في عام 1974 بواسطة بيير ديلين.[14]
من منتصف القرن العشرين إلى أواخره: التطورات في نمطية وأساليب بي-إسيد وما بعدها
بين عامي 1965 و1957، يوتاكا تانياما وغورو شيمورا (المعروف الآن باسم مبرهنة تمطية) التي تربط المنحنيات الناقصة إلى أشكال معيارية.[15][16] يؤدي هذا الارتباط في النهاية إلى الدليل الأول فيرما الأخير طورها أندرو من نظرية فيرما الأخيرة في نظرية الأعداد من خلال الجبر تقنيات هندسة الرفع المعيارية التي طورها أندرو وايليز.[17]
في الستينات، قدم تعميمات المنحنيات المعيارية منذ 1979،[18] لعبت أصناف شيمورا دورا مهما في لانجلاندز برنامج كمجال طبيعي من الأمثلة للاختيار التخمين.[19]
في ورقات في عامي 1977 و1978، أثبت باري مازور الإلتواء لتخمين يعطي قائمة كاملة بالإلتواء المحتمل في ورقات في مجموعات فرعية من المنحنيات الناقصة على الاعداد النسبية. مازور اعتمد الدليل الأول لهذه النظرية على تحليل كامل من النقاط المنطقية على منحنيات معيارية معينة.[20][21] في عام 1996، أور جيم بواسطة معيارية معينة الأرقام تم تمديد إثبات تخمين الالتواء إلى جميع حقول لويك ميريل.[22]
في عام 1983، أثبت جيرد فالتينجز تخمين مورديل، مما يدل على أن منحنى الجنس الأكبر له فقط عدد محدود حيث توجد نظرية من النقاط المنطقية يوضح فقط الجيل المحدود لمجموعة النقاط المنطقية مقابل التحديد.[23][24]
في عام 2001، تم إثبات تخمين معينة من شيمور المحلي لي كان يعتمد على هندسة أصناف معينة من شيمورا.[25]
في عام 2010، طور مساحات ونظريات الكوهومولوجيا الجديدة في الهندسة الحسابية فوق الحقول من التطبيق على تمثيلات وبعض حدسية الوزن أحان حالات تخمين أحادي الوزن.[26][27]
انظر أيضًا
مراجع
- "ساذرلاند ، أندرو ف. (5 سبتمبر 2013)." (PDF)، مؤرشف من الأصل (PDF) في 08 يناير 2016.
- "معلومات عن المعادلة الحسابية على موقع ams.org"، ams.org، مؤرشف من الأصل في 27 أكتوبر 2020.
- "بيورن بونين، تم الاسترجاع في 22 مارس، 2019." (PDF)، مؤرشف من الأصل (PDF) في 07 مايو 2021.
- "arithmetic geometry in nLab"، ncatlab.org، مؤرشف من الأصل في 24 يونيو 2021، اطلع عليه بتاريخ 08 أغسطس 2021.
- Lang, Serge (1997)، Survey of Diophantine Geometry، شبغنكا، ص. 43–67، ISBN 3-540-61223-8، Zbl 0869.11051.
- Mordell, Louis J. (1969)، Diophantine Equations، Academic Press، ص. 1، ISBN 978-0125062503.
- Gowers, Timothy؛ Barrow-Green, June؛ Leader, Imre (2008)، The Princeton companion to mathematics، Princeton University Press، ص. 773–774، ISBN 978-0-691-11880-2، مؤرشف من الأصل في 3 أغسطس 2021.
- A. Weil, L'arithmétique sur les courbes algébriques, Acta Math 52, (1929) p. 281-315, reprinted in vol 1 of his collected papers (ردمك 0-387-90330-5).
- Zariski, Oscar (2004) [1935]، Abhyankar, Shreeram S.؛ Lipman, Joseph؛ Mumford, David (المحررون)، Algebraic surfaces، Classics in mathematics (ط. second supplemented)، Berlin, New York: شبغنكا، ISBN 978-3-540-58658-6، MR 0469915، مؤرشف من الأصل في 09 يوليو 2021.
- Weil, André (1949)، "Numbers of solutions of equations in finite fields"، Bulletin of the American Mathematical Society، 55 (5): 497–508، doi:10.1090/S0002-9904-1949-09219-4، ISSN 0002-9904، MR 0029393. Reprinted in Oeuvres Scientifiques/Collected Papers by André Weil (ردمك 0-387-90330-5)
- Serre, Jean-Pierre (1955)، "Faisceaux Algebriques Coherents"، The Annals of Mathematics، 61 (2): 197–278، doi:10.2307/1969915، JSTOR 1969915.
- Grothendieck, Alexander (1960)، "The cohomology theory of abstract algebraic varieties"، Proc. Internat. Congress Math. (Edinburgh, 1958)، مطبعة جامعة كامبريدج، ص. 103–118، MR 0130879.
- Grothendieck, Alexander (1995) [1965]، "Formule de Lefschetz et rationalité des fonctions L"، Séminaire Bourbaki، Paris: جمعية رياضيات الفرنسية ، ج. 9، ص. 41–55، MR 1608788.
{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link) - Deligne, Pierre (1974)، "La conjecture de Weil. I"، Publications Mathématiques de l'IHÉS، 43 (1): 273–307، doi:10.1007/BF02684373، ISSN 1618-1913، MR 0340258، مؤرشف من الأصل في 07 مايو 2021.
- Taniyama, Yutaka (1956)، "Problem 12"، Sugaku (باللغة اليابانية)، 7: 269.
- Shimura, Goro (1989)، "Yutaka Taniyama and his time. Very personal recollections"، The Bulletin of the London Mathematical Society، 21 (2): 186–196، doi:10.1112/blms/21.2.186، ISSN 0024-6093، MR 0976064.
- Wiles, Andrew (1995)، "Modular elliptic curves and Fermat's Last Theorem" (PDF)، Annals of Mathematics، 141 (3): 443–551، CiteSeerX 10.1.1.169.9076، doi:10.2307/2118559، JSTOR 2118559، OCLC 37032255، مؤرشف من الأصل (PDF) في 15 ديسمبر 2017.
- Shimura, Goro (2003)، The Collected Works of Goro Shimura، Springer Nature، ISBN 978-0387954158.
- Langlands, Robert (1979)، "Automorphic Representations, Shimura Varieties, and Motives. Ein Märchen" (PDF)، في Borel, Armand؛ Casselman, William (المحررون)، Automorphic Forms, Representations, and L-Functions: Symposium in Pure Mathematics، Chelsea Publishing Company، ج. XXXIII Part 1، ص. 205–246.
- Mazur, Barry (1977)، "Modular curves and the Eisenstein ideal"، Publications Mathématiques de l'IHÉS، 47 (1): 33–186، doi:10.1007/BF02684339، MR 0488287، مؤرشف من الأصل في 18 فبراير 2020.
- Mazur, Barry (1978)، with appendix by Dorian Goldfeld، "Rational isogenies of prime degree"، Inventiones Mathematicae، 44 (2): 129–162، Bibcode:1978InMat..44..129M، doi:10.1007/BF01390348، MR 0482230.
- Merel, Loïc (1996)، "Bornes pour la torsion des courbes elliptiques sur les corps de nombres" [Bounds for the torsion of elliptic curves over number fields]، Inventiones Mathematicae (باللغة الفرنسية)، 124 (1): 437–449، Bibcode:1996InMat.124..437M، doi:10.1007/s002220050059، MR 1369424.
- Faltings, Gerd (1983)، "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" [Finiteness theorems for abelian varieties over number fields]، Inventiones Mathematicae (باللغة الألمانية)، 73 (3): 349–366، Bibcode:1983InMat..73..349F، doi:10.1007/BF01388432، MR 0718935.
- Faltings, Gerd (1984)، "Erratum: Endlichkeitssätze für abelsche Varietäten über Zahlkörpern"، Inventiones Mathematicae (باللغة الألمانية)، 75 (2): 381، doi:10.1007/BF01388572، MR 0732554.
- Harris, Michael؛ Taylor, Richard (2001)، The geometry and cohomology of some simple Shimura varieties، Annals of Mathematics Studies، دار نشر جامعة برنستون، ج. 151، ISBN 978-0-691-09090-0، MR 1876802، مؤرشف من الأصل في 24 مايو 2021.
- "Fields Medals 2018"، الاتحاد الدولي للرياضيات، مؤرشف من الأصل في 14 أبريل 2021، اطلع عليه بتاريخ 02 أغسطس 2018.
- Scholze, Peter، "Perfectoid spaces: A survey" (PDF)، University of Bonn، مؤرشف من الأصل (PDF) في 07 مارس 2021، اطلع عليه بتاريخ 04 نوفمبر 2018.
- بوابة رياضيات