هندسة إقليدية
الهندسة الإقليدية (بالإنجليزية: Euclidean geometry) هي نظام رياضياتي يُنسَب إلى إقليدس الإسكندري، التي وضع أسسها في كتابه عن الهندسة: العناصر.[1][2][3] طرق إقليدس تتكون من افتراض مجموعة بسيطة من المُسلّمات البدهية، واستنتاج باقي المُبرهنات منها. مع أن النتائج التي توصل لها إقليدس سبقه إليها رياضياتيون قُدماء، إقليدس كان أول من وضع تلك المبرهنات في نظام منطقي مُحكَم. كتاب العناصر يبدأ بالهندسة المُستوية وهي التي لا تزال تُدرّس في المرحلة الثانوية بصفتها أول نظام مُسلّمات وأول الأمثلة على البرهنة الرسمية. الهندسة الإقليدية تشمل أيضاً الهندسة الفراغية ثلاثية الأبعاد. علاوةً على ذلك، كثيرٌ من النتائج في كتاب العناصر تندرج تحت ما يُسمّى حالياً بالجبر ونظرية الأعداد إلا أنّها مشروحة في لغة هندسية.

لأكثر من ألفي سنة، إطلاق وصف «إقليدية» لم يكن ضرورياً بسبب عدم وجود أنواع أخرى من الهندسة. مُسلّمات إقليدس بّدت واضحةً جليّاً (مع الاستثناء الممكن لمُسلّمة التوازي) لدرجة أنّ أي مبرهنة مُستقاة منها كانت تُعدّ صحيحةً إطلاقاً. بيد أنّه حالياً تُعرَف هندسات أُخرى لاأقليدية مُتّسقة. أولاها اكتُشِفَت في بداية القرن التاسع عشر.
إحدى مقتضيات نظرية آينشتاين عن النسبية العامة أن الحالة الفيزيائية للفضاء ليست إقليدية، وأنّ الفضاء الإقليدي هو تقريب جيد لها فقط ضمن المسافات القصيرة (بالنسبة لقوة مجال الجاذبية).
الهندسة الإقليدية هي إحدى الأمثلة على الهندسة التركيبية في أنّها تسير منطقياً من مسلمات تصف خواصّاً بسيطةً عن الأجسام الهندسية كالنقاط والخطوط، إلى مبرهنات عن تلك الأجسام دون استعمال نُظمٍ إحداثيّةٍ لوصفها. هذا على عكس الهندسة التحليلية التي تُوظّف النظم الإحداثية في ترجمة المبرهنات الهندسية إلى صيغ جبرية.
العناصر
كتاب العناصر بصورة رئيسة كان تنظيماً للمعارف السابقة عن الهندسة. تحسينها لطرق الحل السابقة اشتهرت سريعاً نتيجةَ قلّة الاهتمام في الاحتفاظ بالمنشورات السابقة عن الهندسة التي ضاعت أغلبها.
العناصر يتألّف من 13 مُجلّداً. تُناقش الكتب 1-4 الهندسة المستوية. العديد من النتائج عن المستوى تضمنت معها براهين. على سبيل المثال، «في أي مثلث، مجموع أي زاويتين فيه أقل من مجموع زاويتين قائمتين.» (الكتاب الأول، الفرضية 17) وكذلك مبرهنة فيثاغورس: «مربع الضلع المقابل للزاوية القائمة يساوي مجموع مربعي الضلعين الآخرين.» (الكتاب الأول، المبرهنة 47)
تضمنت الكتب 5 و7 حتى 10 حقائق عن نظرية الأعداد مع التعامل مع الأعداد على أنها أطوال قطع مستقيمة أو مساحات أشكال ما. عرّفت تلك الكتب مفاهيم مثل الأعداد الأولية، الأعداد النسبية وغير النسبية. ومن البراهين الشهيرة هو برهان لانهائية الأعداد الأولية.
الكتب 11-13 تضمنت الهندسة الفراغية. من النتائج الاعتيادية المذكورة هي نسبة حجم القمع للأسطوانة المشتركين في الارتفاع والقاعدة نفسهما.
المُسلّمات
الهندسة الإقليدية هي نظام من المُسلّمات تُشتَقٌ من خلاله جميع المبرهنات. إلى حين مجيئ الهنديات اللاإقليدية، كانت هذه المسلمات تُعتَبر صحيحة بَدَهيّاً في العالم الفيزيائي. براهين إقليدس من الافتراض حتى الاستنتاج بقيت صحيحة بغض النظر عن صحّتها فيزيائيّاً.
منذ بدايات أول كتاب من العناصر، إقليدس أعطى خمس مُسلّمات للهندسة المستوية موصوفة بالنسبة للإنشاءات:
ليكن الآتي مُسلّماً به:
- إمكانية رسم خط مستقيم من أي نقطة إلى أي نقطة.
- إمكانية مدّ قطعة مُستقيمة في خط مستقيم
- إمكانية رسم دائرة بأي مركز وأي شعاع.
- جميع الزوايا القائمة متساوية.
- مُسلّمة التوازي: إذا تقاطع خط مستقيم مع خطين مستقيمين آخرين مُنشئاً زوايا على الجهة نفسها مجموعها أقل من مجموع زاويتين قائمتين، فإنّ هذين الخطين المستقيمين يلتقيان في الجهة التي تكون فيهما مجموع الزاويتين أقل من زاوية قائمة.
على الرغم من أن إقليدس يزعم بوجود الأجسام الهندسية المنشأة، إلا أنّ براهينه الرياضية تفترض ضمنيّاً أن هذه الأجسام الهندسية وحيدة.
كتاب العناصر يتضمن أيضاً «المفاهيم المشتركة» الخمسة:
- الأشياء التي تُساوي الشيءَ نفسَه تساوي بعضها البعض أيضاً (خاصيّة التعدي لعلاقة إقليدية)
- إذا أُضيفت مُتساويات إلى مُتساويات، فإنّ الكُلّ يُساوي الكُلّ. (خاصية التجميع للتساوي)
- إذا طُرحت مُتساويات من مُتساويات، فإن الكل يُساوي الكل. (خاصية الطرح للتساوي)
- الأشياء التي تنطبق مع بعضها تساوي بعضها بعضاً. (خاصية الانعكاس)
- الكُلّ أكبر من الجزء.
العلماء المُعاصرين يتفقون أن مُسلّماتِ إقليدس لا تُوفّر الأساس الكامل الذي يتطلبه إقليدس لبراهينه. ولذلك، فإنّ المعالجات والإصلاحات الحديثة للهندسة الإقليدية تتضمن مجموعة أكبر وأشمل من المُسلّمات.
مُسلّمة التوازي
بالنسبة للقدماء، مُسلّمة التوازي بّدت أقلّ بداهةً من الأخريات. كانوا يأملون إنشاء نظام من مُسلّمات قاطعة تماماً. بمنظورهم، ظهرت مسلّمة التوازي وكأنها مُبرهنة تحتاج لبرهان من جُمَل أبسط. بات اليوم معروفاً أن البرهان لذلك مستحيل، لأنه بالإمكان إنشاء أنظمة مُتّسقة من الهندسة التي قد تكون فيها مسلمة التوازي صحيحة وقد تكون خاطئة. إقليدس بنفسه تعامل مع المسلمة بنحوٍ مُختلف عن بقية المسلمات عندما كتب أول 28 مبرهنة دون استعمال مبرهنة التوازي.
هناك العديد من المُسلّمات التي بالإمكان صياغتها لتكون مُتطابقة منطقياً مع مُسلّمة التوازي (في سياق المُسلّمات الأخرى نفسه). على سبيل المثال، مُسلّمة بلاي فير تنص على أنّ:
في المُستوى، لأي نُقطة لا تقع على خط مُستقيم مُعطى، ثمّة خط واحد على الأكثر لا يلتقي الخط المُعطى.
عبارة «على الأكثر» هي كل ما تحتاجه المُسلّمة، لأنه بالإمكان إثبات من خلال المٌسلّمات الأخرى أن هناك خط موازي واحد على الأقل.
طرق البرهنة
الهندسة الإقليدية هندسة إنشائية. المسلمات 1، 2، 3، و5 تزعم وجود ووحدانية بعض الأجسام الهندسية وهذه الافتراضات إنشائية الطبيعة. بمعنى أنه ليس فقط هذه الأجسام الهندسية موجودة، بل وأننا نعلم طريقة إنشائها باستعمال المسطرة والفرجار فقط. بهذا المعنى، الهندسية الإقليدية أكثر عينيةً وصلادة من العديد من نظم المُسلمات كنظرية المجموعات، التي عادةً تفترض وجود أجسام دون شرح طريقة إنشائها، أو حتّى تفترض أنها غير قابلة للإنشاء في النظرية. من منظور أكثر صرامة، الخطوط على الورق هي مجرد نماذج للأجسام المُعرفة ضمن النظام الرسمي، بدلاً من كونها أمثلة من تلك الأجسام. على سبيل المثال، الخط المستقيم الإقليدي ليس له سُمك، لكن أي خط واقعي سيكون له. غالب الرياضياتيين يعتبرون طرق البرهان غير الإنشائية لها نفس صحة البراهين الإنشائية.
إقليدس كثيراً ما استعمل البرهان بالتناقض. الهندسة الإقليدية تسمح كذلك بوجود الموقع الفائق، الذي يكون فيه الشكل مُزاحاً لموقعٍ آخر في المستوى. مثلاً، المبرهنة الرابعة: تطابق ضلع-زاوية-ضلع للمثلث إثباته بتحريك أحد المثلثين بحيث أضلاعه تنطبق على ضلعين من الآخر، ثم إثبات أنّ الضلع الأخير منطبق أيضاً. بعض الإصلاحات الحديثة في الهندسة أضافت مُسلّمةً سادسة: تصلُّب المُثلث، والتي اقتُرحَت بديلاً للموقع الفائق.
نظام القياس والحساب
الهندسة الإقليدية تتضمن اثنين من أنواع القياس الأساسية: الزاوية، والمسافة. قياس الزاوية قياسٌ مُطلقٌ. استعمل إقليدس الزاوية القائمة بوصفها وحدته الأساسية. بحيث أن الزاوية 45 يُشار إليها بنصف زاوية قائمة مثلاً. على الوجه المقابل، قياس المسافة نسبي. بإمكان اختيار أي قطعة مستقيمة لامنعدمة على أنها وِحدةُ الطول المُستعملة وبقية الأطوال يُعبّرُ عنها بالنسبة لها. جمع الأطوال يُمثّل بإنشاء تكون فيه قطعة مستقيمة منسوخة إلى الطرف الآخر من قطعةٍ مُستقيمةٍ أخرى، وبالمثل للطرح. قياسات المساحة والحجم تُشتَقُّ من المسافات. مثلاً، المستطيل ذو الطول 3 وحدات والعرض 4 وحدات له مساحة تبلغ 12 وحدة مربعة. لأن هذا المفهوم الهندسي من الضرب كان محدوداً ضمن إطار التصور الهندسي، لم يكن هناك طريقة مباشرة لتفسير حاصل ضرب 4 أعداد فأعلى. ولذا يُرَى أن إقليدس تجنّب مثل حواصل الضرب هذه على الرغم من احتواء براهينها بها ضمنياً، مثلاً في كتابه السادس، المبرهنة 20. إقليدس يُشير إلى أزواج المستقيمات أو الأشكال، سواءً المُسطّحة أو المُجسّمة، على أنها متساوية (ἴσος) إذا كانت أطوالها، مساحاتها، أو أحجامها متساوية توالياً، وبالمثل للزوايا. المصطلح «متطابق» هو المُصطلح المُحبّذ وهو يُشير إلى مفهوم أن أي جسم هندسي له نفس الشكل والحجم أو المساحة لشكل آخر، بحيث أنه بالإمكان قلبه أو تحريكه بحيث ينطبق على الآخر. على سبيل المثال، المستطيلات ذات الأبعاد 2×6 و 3×4 متساوية المساحة لكنها ليست متطابقة. لكن الحرف «س» وصورته في المرآة شكلان متطابقان. الأشكال المتطابقة لكنها تختلف في أحجامها يُشار إليها بأنها «مُتشابهة». الزوايا المتناظرة في أزواج الأشكال المُتشابهة متطابقة، والأضلاع متناسبة في الطول.
الترميز والتسمية
تسمية النقاط والأجسام جرت العادة بتسمية النقاط باستعمال الأحرف اللاتينية الكبيرة (بالإنجليزية: Capital letters) أما بقية الأشكال، كالخطوط، المثلثات أو الدوائر تُسمّى بتعداد عددٍ كافٍ من النقاط التي تُمثّلها دون لبس. مثلاً، المثلث ABC يُطلق على المثلث ذو الرؤوس A، B، وC.
الزوايا المتكاملة والمتتامة الزوايا التي مجموعها زاوية قائمة تُسمّى مُتتامّة. الزوايا المتتامة تُنشئ عند انطلاق شعاع من رأس زاويةٍ قائمةٍ. عدد الأشعّة بين شُعاعين لامنتهٍ. الزوايا التي مجموعها زاوية مستقيمة تُسمّى زوايا متكاملة. الزوايا المتكاملة تُنشَئ عندما يُطلع شعاع من نقطة على خطٍ مُستقيم.
الأجسام الهندسية
النقطة
لا حاجة لتعريف النقطة بواسطة مصطلحات وإنما يمكن تعريفها بواسطة بديهية معينة، كما يمكن تعريفها على أنها كل ما ليس له جزء أو كل مايمكن إهمال أبعاده الثلاثة ويعبر عنها هندسيا بالأثر الذي يتركه القلم عند الضغط عليه بدون تحريكه. أو هي تقاطع خطين مستقيمين.
المستقيم
هو عدد لا متناهي من النقاط التي تقع علي مستوى واحد وتصل بين أي نقطتتين.
نصف مستقيم
يطلق عليه أيضا اسم «الشعاع» وهو جزء من مستقيم محدد بنقطة تسمى أصل نصف المستقيم.له بداية وليس له نهاية ويتكون من عدد غير نهائى من النقاط
مسلمات إقليدس
- من نقطتين يمر مستقيم وحيد.
- يمكن إنشاء خط مستقيم من خلال تمديد نهايتي قطعة مستقيمة من الجهتين إلى ما لانهاية.
- يمكن رسم دائرة من خلال نقطة مركز ونصف قطر.
- كل الزوايا القائمة متساوية فيما بينها.
- (مسلمة التوازي) إذا قطع مستقيم مستقيمين وكان مجموع الزاويتين المتقابلتين عند جهة القاطع أقل من مجموع زاويتين قائمتين (أقل من 180°) وعند مد هذين المستقيمين من جهة الزاويتين فسوف يتقاطعان.
إنشاءات هندسية
لا تستعمل الهندسة الإقليدية سوى المسطرة والفرجار لإنشاء الأشكال وهذا أدى إلى ظهور مسائل هندسية لم يتم حلها إلا في القرن 19 وهذه المسائل هي:
- تقسيم زاوية إلى ثلاثة أقسام متساوية.
- إنشاء مكعب حجمه ضعف حجم مكعب معلوم.
- إنشاء مربع مساحته تساوي مساحة دائرة معينة.
و هذه المسائل يستحيل حلها باستعمال المسطرة والفرجار فقط.
بواسطة المسطرة والفرجار يمكن إنشاء ما يلي:
- مستقيمين متوازيين
- مستقيمين متعامدين
- منصف زاوية
- واسط قطعة
- دائرة
- قطعة طولها جداء طول قطعتين
- قطعة طولها خارج قسمة طول قطعتين
- قطعة طولها جذر مربع طول قطعة معينة
- زاويتان متساويتان.
طرق الإثبات
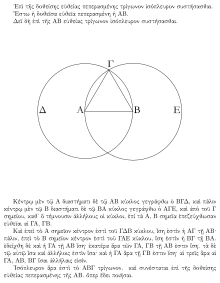
مراجع
- "معلومات عن هندسة إقليدية على موقع britannica.com"، britannica.com، مؤرشف من الأصل في 27 يناير 2018.
- "معلومات عن هندسة إقليدية على موقع jstor.org"، jstor.org.
- "معلومات عن هندسة إقليدية على موقع d-nb.info"، d-nb.info، مؤرشف من الأصل في 2 مايو 2021.
- بوابة رياضيات
- بوابة هندسة رياضية
| جزء من سلسلة مقالات حول |
| الهندسة الرياضية |
|---|
 |
|
| علماء الهندسة |
| بوابة هندسة رياضية |

