خماسي أضلاع
في الهندسة الرياضية، خُمَاسِيّ الأَضْلاَعِ[1] أو المُخَمَّس[1][2] (بالإنجليزية: Pentagon) هو مضلع له خمسة أضلاع.[3][4][5] مجموع الزوايا الداخلية لخماسي أضلاع بسيط (أي أضلاعه لا تتقاطع مع بعضها البعض) ومحدب يساوي 540 درجة.
مخمس 
|
مخمس منتظم | |
|---|---|
 مخمس منتظم | |
| أضلاع ورؤوس | 5 |
| رمز شليفلي | {5} |
| مخطط كوكستير-دينكين | |
| مجموعة التناظر | تناظر ثنائي السطوح (D5) |
| زاوية داخلية (درجة) | 108° |
| خصائص | محدب، مضلع دائري، منتظم، رأسي، متعدي الحافة |

الصفحة 34 من كتاب فيما یحتاج إليه الصانع من أعمال الهندسة لأبي الوفاء البوزجاني حيث يذكر فيها كيفية رسم مخمس في دائرة
قد يكون خماسي الأضلاع بسيطا وقد يكون ذاتي التقاطع. خماسي ذاتي التقاطع يسمى نجمة خماسية.
الخماسي المنتظم

خطوات إنشاء المخمس باستخدام الفرجار والمسطرة.
- الزاوية الداخلية للخماسي تساوي 108°.
مساحة خماسي منتظم
- تعطى مساحة المخمس ذو طول الضلع t بالعلاقة التالية:
تعطى مساحة المخمس بدلالة نصف قطر الدائرة المحاطة داخله r بالعلاقة:
.
إنشاء خماسي منتظم
المخمس هو مضلع قابل للإنشاء باستخدام إنشاءات الفرجار والمسطرة. ويعود ذلك إلى كون 5 عددا أوليا لفيرما. هناك العديد من الطرق اللائي يمكنن من إنشاء خماسي منتظم. منهن ما يلي.
طريقة ريشموند


دوائر كارليل

رسم خماسي باستعمال دوائر كارليل
البرهان على أن cos 36° =
- ليكن u = cos 36°. أولا لاحظ أن
0 < u < 1 (والتي ستساعدنا في التبسيط أثناء العمل). الآن،
قد يعبر عن هذه النتيجة نثرا كما يلي :
الجيب التمام لزاوية تساوي ستة وثلاثين درجة هو نصف النسبة الذهبية.
أمثلة عن الخماسيات
نباتات
 المقطع العرضي للبامية.
المقطع العرضي للبامية. مجد الصباح، مثل العديد من الزهور الأخرى ، لها شكل خماسي.
مجد الصباح، مثل العديد من الزهور الأخرى ، لها شكل خماسي. يحتوي متاع التفاح على خمس نقرات ، مرتبة بنجمة ذات خمس فروع.
يحتوي متاع التفاح على خمس نقرات ، مرتبة بنجمة ذات خمس فروع.
حيوانات
 نجم البحر، مجموعة من شوكيات الجلد لها تماثل خماسي.
نجم البحر، مجموعة من شوكيات الجلد لها تماثل خماسي.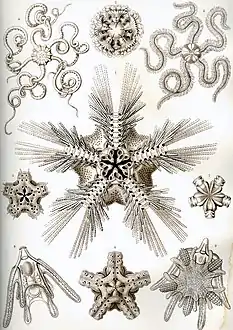 رسم توضيحي لنجم البحر الهش، أيضا من شوكيات الجلد اللائي لهن شكل خماسي.
رسم توضيحي لنجم البحر الهش، أيضا من شوكيات الجلد اللائي لهن شكل خماسي.
معادن
 الشبه بلورة "Ho-Mg-Zn" عشرينية الأوجه تشكلت كاثنا عشري سطوح خماسي الشكل. الوجوه كلها خماسيات منتظمة.
الشبه بلورة "Ho-Mg-Zn" عشرينية الأوجه تشكلت كاثنا عشري سطوح خماسي الشكل. الوجوه كلها خماسيات منتظمة. بلورة بيريت، عبارة عن اثنا عشري الوجوه له 12 وجهًا خماسيًا متطابقًا غير مقيد ليكون منتظمًا.
بلورة بيريت، عبارة عن اثنا عشري الوجوه له 12 وجهًا خماسيًا متطابقًا غير مقيد ليكون منتظمًا.
إنشاءات إنسانية
 بنتاغون، المقر الرئيسي لوزارة دفاع الولايات المتحدة.
بنتاغون، المقر الرئيسي لوزارة دفاع الولايات المتحدة. صفيحة ملعب كرة القاعدة (Home Plate)
صفيحة ملعب كرة القاعدة (Home Plate) كرة قدم أديداس تيليستار، باللونين المعتادين الأبيض والأسود. هي على شكل عشريني أوجه مقطع الرؤوس. ابتكرت في عام 1970. الأشكال السوداء هن خماسيات أضلاع.
كرة قدم أديداس تيليستار، باللونين المعتادين الأبيض والأسود. هي على شكل عشريني أوجه مقطع الرؤوس. ابتكرت في عام 1970. الأشكال السوداء هن خماسيات أضلاع.
المراجع
- ترجمة كلمة pentagon على موقع قاموس المعاني. (تاريخ الاطلاع: 5 نوفمبر 2017) نسخة محفوظة 07 نوفمبر 2017 على موقع واي باك مشين.
- كتاب فيما یحتاج إليه الصانع من أعمال الهندسة لأبي الوفاء البوزجاني.
- "معلومات عن مخمس على موقع babelnet.org"، babelnet.org، مؤرشف من الأصل في 13 ديسمبر 2019.
- "معلومات عن مخمس على موقع vocab.getty.edu"، vocab.getty.edu، مؤرشف من الأصل في 18 أبريل 2020.
- "معلومات عن مخمس على موقع jstor.org"، jstor.org، مؤرشف من الأصل في 26 مايو 2019.
- بوابة رياضيات
- بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.