تحاك
التحاكي (بالإنجليزية: Homothetic transformation) هو عملية نقل رياضي لفضاء ما، بحيث ينقل كل خط إلى خط مواز.[1][2] كل توسع يشكل زمر في الفضاء الاقليدي أو الفضاء التآلفي. من أشهر الأمثلة للتوسع هي الانزلاق، الدوران النصفي والدالة المتطابقة.
في الهندسة الأقليدية، نسبة التكبير هي قيمة مفردة c والتي تستعمل لحساب نسبة التوسع من خلال ضرب كل قيمة بها. وتسمى أيضا: معامل التوسيع أو نسبة الشبه. ويمكن تسمية عملية النقل هذه بالتضخيم [الإنجليزية]. وبشكل أعم، فيمكن ل c أن تكون سالبة، وفي هذه الحالة، تضرب كل المقادير بـ كما تقوم بعكس كل النقاط بالنسبة لنقطة ثابتة.
لشرح المبدأ بمعادلة، فافترض وجود مركز أو مصدر c وعدد حقيقي (ممكن أن يكون سالبا). فإن التحاكي تنقل كل نقطة M إلى نقطة أخرى بحيث:
التحاكي هو عملية نقل تآلفي وبنفس الوقت هي عملية نقل تشابه حيث تضاعف كل المسافات بـ وكل المساحات بـ . أما إذا كانت نقطة المصدر هي نفسها نقطة المركز، فتعد كنقل خطي.
تطبيقات
علاقات التحاكي
إحدى تطبيقات المفهوم هي علاقة التحاكي R والتي تعتبر كذلك إذا كان: لكل بحيث
ومن التطبيقات الاقتصادية لهذه المعادلة أن الدالة البديلة المتجانسة بدرجة 1 تطابق علاقة أفضلية [الإنجليزية] تحاك [الإنجليزية].
تطبيقات اقتصادية
في علم الاقتصاد، دالة التحاكي التي تفصل إلى دالتين: الدالة الخارجية (U(x وهي دالة تحاك من الدرجة 1 ودالة داخلية (f(y وهي دالة متزايدة رتيبة، فإن (U(f(y هي دالة تحاك.
في الهندسة الوصفية
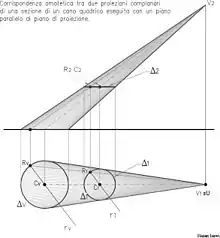
وبالإشارة إلى التمرين المبين في الشكل 2 [3]، من المهم معرفة انه بمجرد ما تم تحديد واحد من الشكلين المتقابلين، نقوم بتكراره عن طريق استخدام مثلا العلاقة التقابلية التي تسمى تحاك أو تحول متماثل (Homothetic transformation). علما بأن جميع أنواع العلاقات التقابلية تتميز بما يلي:
- تصطف جميع النقاط المتقابلة، مثل A, A' و B,B' مع نقطة U تسمى مركز التقابل
- تلتقي جميع الخطوط المتقابلة مثل AB و A على خط يسمى محور التقابل.
وعندما تكون الاشكال المتقابلة متشابهة كما في المثال المرفق، تسمى العلاقة التقابلية تحاكي. التي تتميز بكون محور التقابل خط لانهائي، وهذا يعني ان الخطوط المتقابلة مثل A-B ، A'B تكون متوازية لبعضها البعض. على سبيل المثال وبعد الانتهاء من تحديد الشكل الملون بالأصفر، وبهدف تحديد الشكل المقابل له (الملون بالأخضر)، نقوم بتعيين زوجين من النقاط المتقابلة، مثل A ، A 'و B ، B' .. ومن ثم نشرع بتحديد مركز التقابل U كنقطة تقاطع بين الخطوط التي تمر بتلك النقاط. مثلا لتحديد النقطة C'، نقوم بتوصيلها مع نقطة B معلومة النقطة المقابلة لها B'. وهكذا نحصل على الخط r'. الخط r' المقابل للخط r يمر بالنقطة B' ويكون أيضا موازي للخط r. وأخيرا نحدد النقطة المطلوبة B' كتقاطع بين r' والخط U-B وبطريقة مماثلة للخطوات السابقة من الممكن تحديد جميع نقاط الشكل الأخضر

مراجع
- "معلومات عن تحاك على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 31 مارس 2019.
- "معلومات عن تحاك على موقع thes.bncf.firenze.sbn.it"، thes.bncf.firenze.sbn.it، مؤرشف من الأصل في 14 ديسمبر 2019.
- homothetic transformation نسخة محفوظة 2019-09-28 على موقع واي باك مشين.
انظر أيضًا
- تناظر
- تماثل
- تناسب
- تشابه (هندسة)
- تجانس (هندسة) [الإنجليزية]
- توسع (هندسة) [الإنجليزية]
- محاكاة
- التفاف
- هندسة أفينية
- هندسة إقليدية
- غير إقليدية
- بوابة رياضيات
- بوابة هندسة رياضية