استقرار أسي
في نظرية التحكم، النظام الخطي المستقل زمنيًّا يكون مستقرًّا أسيًّا، إذا وفقط إذا كان لديه متجه خاص (أي أقطاب أنظمة الإدخال للإخراج) بعدد حقيقي سالب فقط (أي في النصف الأيسر من المستوى المركب).[1] نظام خطي مدخل إلى مخرج ومستقل ومتقطع زمنيًّا يكون مستقرًّا أسيًّا إذا وفقط إذا كانت أقطاب دالة التحويل تقع داخل دائرة الوحدة التي مركزها نقطة أصل المستوى المركب. الاستقرار الأسي هو شكل من أشكال الاستقرار التقاربي. والأنظمة التي ليست خطية ومستقلة زمنيًّا تكون مستقرة بشكل كبير إذا كان تقاربها يحده اضمحلال أسي.
- طالع استقرار ليابنوف ، الذي يعطي تعريفًا لـللاستقرار التقاربي بشكل أعم للأنظمة الديناميكية (التحريكية). كما أن جميع الأنظمة المستقرة أسيًا مستقرة تقاربيًّا.
عواقب عملية
النظام الخطي المستقل زمنيًّا المستقر أسيًّا لن ينفجر (أي أنه لن يُعطي مخرجًا غير محدود) إذا أُعطيَ مُدخلًا محدودًا (نهائيًّا) أو شرط أولي غير صفري. علاوةً على ذلك، إذا تم إعطاء النظام مُدخلًا ثابتًا ومحدودًا (مثل دالة هيفيسايد الدرجي) ، فسوف يتحلل إلى تذبذبات تتحلل بمعدل أسي، وسوف يميل الناتج بشكل تقاربي إلى قيمة نهائية ثابتة وجديدة. إذا تم إعطاء النظام دفعة من الدوال النبضية كمدخل بدلاً من ذلك، فسوف تتلاشى التذبذبات المستحثة وسيعود النظام إلى قيمته السابقة. إذا لم تتلاشى التذبذبات، أو لم يعد النظام إلى ناتجه الأصلي عند تطبيق دفعة من الدوال النبضية، فإن النظام يكون مستقرًا بشكل هامشي بدلاً من ذلك.
أمثلة على أنظمة خطية ومستقرة زمنيًّا تكون مستقرة أسيًّا
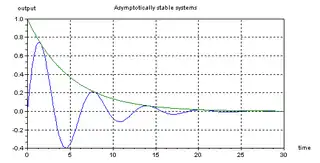
يُظهر الرسم البياني الذي على اليسار، استجابة نبضية لنظامين مختلفين. المنحنى الأخضر يُمثل الاستجابة النبضية لـ، بينما يُمثل المنحنى الأزرق الاستجابة النبضية لـ، على الرغم من أن هناك استجابة تذبذبية في النظام، إلا أن كلاهما يعودان إلى القيمة الأصلية 0 مع مرور الوقت.
مثال من حياتنا اليومية
تخيل وضعك رخامًا في مغرفة. سيستقر الرخام في أدنى نقطة من المغرفة وسيبقى هناك ما لم تُؤثر عليه قوة خارجية. تخيل الآن إعطاءك المغرفة دفعةً قديرة، وهو تقريب لقوة الدالة النبضية. سوف يتدحرج الرخام ذهابًا وإيابًا، ولكن في النهاية سيستقر في قاع المغرفة. إن رسم الوضع الأفقي للرخام بمرور الوقت سيعطيك استجابة دالة الجيب المتناقصة تدريجيًّا مثل المنحنى الأزرق في الصورة أعلاه. يتطلب الإدخال التدريجي (طالِع: دالة الوحدة والدالة الدرجية) في هذه الحالة دعم الرخام بعيدًا عن الجزء السفلي من المغرفة، بحيث لا يمكنه التراجع. سيبقى في نفس الوضع ولكن لن يستمر، كما هو الحال إذا كان النظام مستقرًا بشكل هامشي أو غير مستقر تمامًا، والذي يحدث عند مواصلة الابتعاد عن الجزء السفلي من المغرفة تحت تأثير تحت القوة الثابتة (والتي تكون مساوية لوزنه). من المهم ملاحظة أن النظام في هذا المثال غير مستقر لجميع المدخلات. للتوضيح، أعطِ الرخام دفعةً قويةً جدًّا، وستكون كفيلة بإصقاطه من المغرفة، وتوقفه فقط عندما يصل إلى الأرضية. لذلك، بالنسبة لبعض الأنظمة، من المناسب أن نقول إن النظام مستقر بشكل كبير عبر نطاق معين من المدخلات فقط.
طالِع ايضًا
مراجع
- ديفيد ن. شيبان (2004)، الجاذبون العالميون للأنظمة الديناميكية (التحريكية) التبادلية غير المستقلة. صفحة 47
روابط خارجية
- تقدير العوامل وتصفية الاستقرار التقاربي[وصلة مكسورة]، أنستافيا باباسلفيو - 28 أيلول (سبتمبر) 2004
- بوابة علم الأنظمة