قطب (تحليل عقدي)
في التحليل العقدي، قطب (بالإنجليزية: Pole) دالة جزئية الشكل هو نوع ما من خصوصية تتصرف كما تتصرف خصوصية الدالة عندما يكون z مساويا للصفر.[1] إذا كان a قطبا لدالة ما (f(z، فإن هذه الدالة تؤول إلى ما لا نهاية له عندما يقترب z من a.
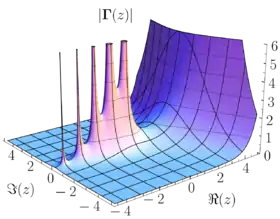
القيمة المطلقة لدالة غاما. هذا الشكل يشير إلى أن الدوال تؤول إلى ما لا نهاية له عند الأقطاب (اليسار). في اليمين، دالة غاما ليس لها أقطاب بل تتصاعد بوتيرة كبيرة.
تعريف
ليكن U مجموعة مفتوحة من المستوى العقدي C وليكن a عنصرا من U ولتكن f دالة f : U \ {a} → C، حيث f دالة تامة الشكل على نطاقها. إذا وجدت دالة g تامة الشكل g : U → C حيث (g(a مختلف عن الصفر، ووجد عدد صحيح موجب n حيث يتوفر ما يلي مهما كان z في {U \ {a:
فإن a يسمى قطبا للدالة f.
أمثلة
- الدالة
- لها قطب من الدرجة الأولى 1 (قطب بسيط) عند .
- الدالة
- لها قطب من الدرجة الثانية عند وقطب من الدرجة الثالثة عند .
- الدالة
- لها أقطاب من الدرجة الأولى 1 عند من أجل مشاهدة ذلك، اكتب على شكل متسلسلة تايلور حول أصل المعلم.
- الدالة
- له قطب وحيد عند ما لا نهاية له، وهو من الدرجة الأولى.
انظر أيضا
مراجع
- "معلومات عن قطب (تحليل عقدي) على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 9 يونيو 2019.
- بوابة تحليل رياضي
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.