دالة غاما
في الرياضيات، دالة غاما (بالإنجليزية: Gamma function) (والممثلة عموما بالحرف Γ، الحرف اليوناني الكبير غاما) هي امتداد لدالة المضروب في الأعداد الحقيقية والمركبة.[1][2][3] إذن، دالة غاما هي دالة تحقق ما يلي بالنسبة عدد صحيح موجب n:
| دالة غاما | |
|---|---|
 تمثيل لدالة غاما على الإحداثيات الديكارتية تمثيل لدالة غاما على الإحداثيات الديكارتية | |
| تدوين | |
| تعريف الدالة | |
| مشتق الدالة | ، حيث هي دالة بوليغاما [الإنجليزية]. |
| الميزات الأساسية | |
| مجال الدالة | |
| قيم محددة | |
| القيمة/النهاية عند الصفر |
|
| نهاية الدالة عند +∞ | +∞ |
| القيمة/النهاية عند 1 | 1 |
| القيمة/النهاية عند 12 | |
| القيمة/النهاية عند 32 | |
| القيمة/النهاية عند 52 | |
| القيمة/النهاية عند 4 | 6 |
| خطوط مقاربة | مع |
| نقاط ثابتة | 1، و 3.562...، ... وغيرها |
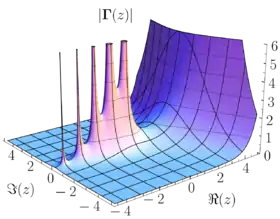
دالة غاما هي دالة معرفة عند جميع الأعداد المركبة باستثناء الأعداد الصحيحة السالبة. فللعدد z الذي يتكون من جزء حقيقي موجب تعرف دالة غاما كما يلي: حيث .
دانييل برنولي هو من اكتشف هذه الصيغة.
ويمكن أن يمتد هذا التعريف بالامتداد التحليلي إلى دالة جزئية الشكل تصير دالة تامة الشكل على المستوى العقدي كله باستثناء الصفر والأعداد الصحيحة السلبية حيث للدالة أقطاب بسيطة.
انظر إلى تحويل ميلين.
هناك دوال أخرى تمدد دالة العاملي، ولكن دالة غاما هي الأكثر شيوعا ونفعا. تظهر في العديد من دوال التوزيعات الاحتمالية، مما يجعلها مهمة في مجالات الاحتمال والإحصاء كما في مجال التوافقيات.
أهداف تعريف دالة غاما
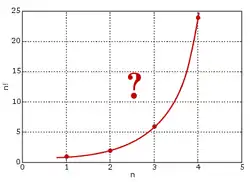
يمكن أن يُنظر إلى دالة غاما حلحلةً لمعضلة الاستيفاء التالية:
- من هو المنحنى القابل للاشتقاق الذي يربط جميع النقط (x, y) حيث y = (x − 1)! كلما كان x عددا صحيحا طبيعيا موجبا قطعا؟
تعريف
التعريف الأساسي
عالم الرياضيات الفرنسي ليجاندر هو أول من استعمل الرمز (Γ(z. باستعمال التكامل بالتجزيء، يمكن أن نجد أن دالة غاما تحقق المعادلة التالية :
علما أن 1 = (Γ(z، نحصل على ما يلي:
خصائص
الامتداد باستعمال متسلسلة فورييه
قيم خاصة
فيما يلي بعض من القيم الخاصة لدالة غاما
التاريخ
القرن الثامن عشر : أويلر وستيرلينغ
معضلة تمديد دالة العاملي إلى الأعداد غير الصحيحة درست لأول مرة من طرف كل من دانييل برنولي وكريستيان غولدباخ في عشرينات القرن الثامن عشر. إلا أنها حلحلت من طرف عالم الرياضيات ليونهارت أويلر. كان ذلك في نهاية ذلك العقد ذاته. أعطى أويلر تعريفين اثنين لدالة عاملي. الأول لم يكن تكامله ولكنه كان جداءا غير منته.
والذي أخبر به غولدباخ في رسالة أرسلها إليه في الثالث عشر من أكتوبر عام 1729. كتب أويلر مجددا إلى غولدباخ في الثامن من يناير عام 1730 من إجل إخباره أن توصل إلى صيغة أخرى عل شكل تكامل تساوي دالة العاملي.
انظر إلى جيمس ستيرلينغ وإلى صيغته صيغة ستيرلينغ وإلى جداء غير منته.
القرن التاسع عشر : غاوس وفايرشتراس وليجاندر

أعاد كارل فريدريش غاوس كتابة صيغة أويلر كما يلي:
انظر إلى كارل فايرشتراس وإلى أدريان ماري ليجاندر.
انظر أيضا
- دالة عاملي
- توزيع غاما
- مجموع غاوس
مراجع
- "معلومات عن دالة غاما على موقع id.ndl.go.jp"، id.ndl.go.jp، مؤرشف من الأصل في 9 أغسطس 2020.
- "معلومات عن دالة غاما على موقع psh.techlib.cz"، psh.techlib.cz، مؤرشف من الأصل في 22 نوفمبر 2020.
- "معلومات عن دالة غاما على موقع xlinux.nist.gov"، xlinux.nist.gov، مؤرشف من الأصل في 13 أكتوبر 2018.
وصلات خارجية
- NIST Digital Library of Mathematical Functions:Gamma function
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
- C++ reference for std::tgamma
- Examples of problems involving the gamma function can be found at Exampleproblems.com.
- Hazewinkel, Michiel, المحرر (2001)، "Gamma function"، Encyclopedia of Mathematics، سبرنجر، ISBN 978-1-55608-010-4
- Wolfram gamma function evaluator (arbitrary precision)
- قالب:WolframFunctionsSite
- Volume of n-Spheres and the Gamma Function at MathPages
- إيريك ويستاين، Gamma Function، ماثوورلد Mathworld (باللغة الإنكليزية).
- بوابة رياضيات
- بوابة تحليل رياضي