مشتق (رياضيات)
العدد المُشتَقّ (بالإنجليزية: Derivative) في نقطة، على رسم بياني لدالة ذات متغيرات وقيم حقيقية، هو معامل المماس الموجِّهُ.[1][2][3] يعبر التفاضل عن المعدل الذي تتغير به قيمة y نتيجة تغير قيمة x توجد بينهما علاقة رياضية أو دالة رياضية. وتعرف الدالة المشتقة بأنها ميل المماس لمنحنى (f(x عند أي نقطة بشرط وجود هذه المشتقة أو هي السرعة اللحظية أو معدل التغيير اللحظي للدالة. نستخدم الرمز Δ للدلالة على التغير في الكمية. ويكون معدل التغير هو نهاية نسبة تغير y إلى نسبة تغير x :
| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
 |
| بوابة رياضيات |
عندما Δx تقارب 0.
يمكن أن نكتب مشتق y بالنسبة ل x : (ترميز لايبنز)
التعبير الدقيق عن مفهوم الاشتقاق يكون باستخدام مقادير لا متناهية في الصغر:

التاريخ
يعود تاريخ الحساب متناهي الصغر بشكل عام إلى العصور القديمة، ويرتبط بالرياضيين إسحاق نيوتن وغوتفريد لايبنتس،[4] حيث اكتشفاه في القرن السابع عشر. ومع ذلك نجد أن هذا النوع من الحساب بدأه علماء رياضيات سابقين: أرخميدس وبيير دي فيرما، وخاصة إسحاق بارو.[5]
رمز الاشتقاق
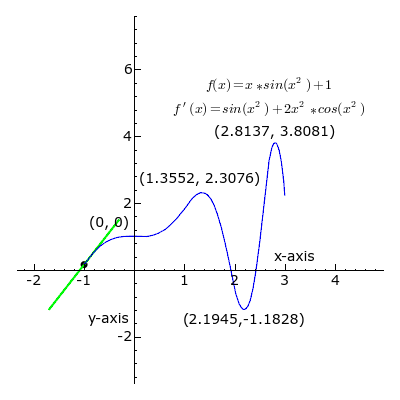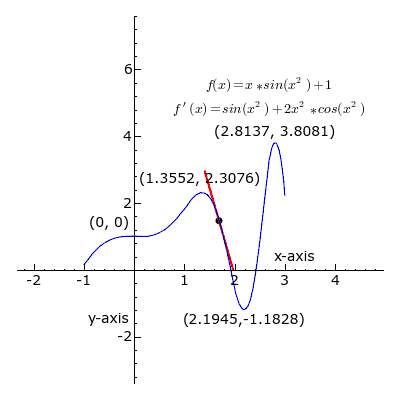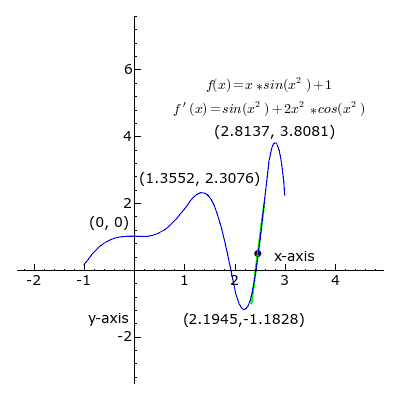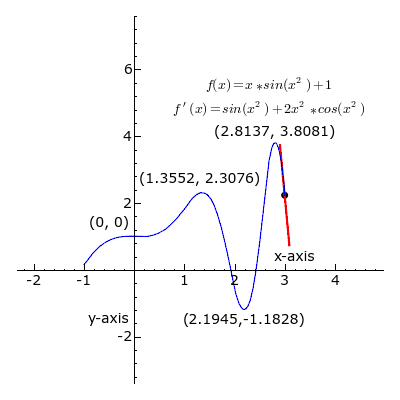
يمكن التعبير عن المشتق بعدة صيغ، منها ما يلي :
صيغة لايبنتز
- ،والتي تكافئ الصيغة
و تُقرأ ((dfdx)) أو ((مشتقة f بدلالة x)) ، أما d(f(x))/dx فتُقرأ ((ddx للدالة f عند x)) أو ((مشتقة f عند x))
dy/dx
و تُقرأ ((dydx)) أو ((مشتقة y بدلالة x))
صيغة لاغرانج
واحدة من الترميزات الأكثر استعمالا في الرياضيات المعاصرة تعود إلى عالم الرياضيات الفرنسي جوزيف لويس لاغرانج.
- أو y'، و تُقرأ الأخيرة مشتقة y.
صيغة إسحاق نيوتن
- أو ،تستعمل خاصة في الفيزياء.
صيغة ليونهارد أويلر
قواعد حساب الدالة المشتقة
الاشتقاق الثابت
في التحليل الرياضي، مشتق ثابت أو تابع ثابت هو الصفر. التابع الثابت هو تابع لا يعتمد على أي متغير مستقل مثل :
f(x) = 7
مشتقات بعض الدوال المعروفة
| الدالة |
المشتقة |
شرط الاشتقاق |
|---|---|---|
|
| ||
| أو | , | |
مراجع
- Evans, Lawrence (1999)، Partial Differential Equations، American Mathematical Society، ص. 63، ISBN 0-8218-0772-2.
- "The Notation of Differentiation"، MIT، 1998، مؤرشف من الأصل في 05 ديسمبر 2017، اطلع عليه بتاريخ 24 أكتوبر 2012.
- Kreyszig, Erwin (1991)، Differential Geometry، New York: Dover، ص. 1، ISBN 0-486-66721-9.
- Bos, H. J. M. (01 مارس 1974)، "Differentials, higher-order differentials and the derivative in the Leibnizian calculus"، Archive for History of Exact Sciences (باللغة الإنجليزية)، 14 (1): 1–90، doi:10.1007/BF00327456، ISSN 1432-0657، مؤرشف من الأصل في 13 مارس 2020.
- Émerand (1860)، Biographie de Tarn-et-Garonne: études historiques et bibliographiques ... (باللغة الفرنسية)، Forestié neveu، مؤرشف من الأصل في 14 يناير 2020.
- بوابة رياضيات
- بوابة تحليل رياضي