تبليط لادوري

التبليط اللادوري (بالإنجليزية: aperiodic tiling)‏ هو نوع من زمر التبليط الذي لا يشكل نمط متتابع. وأي زمرة من البلاط اللادوري يمكن أن يشكل عدد لا نهائي من أشكال التبليط.

تبليط بنروز هو نوع من التبليط اللادوري

مثال على ترتيبات تبليطات بنروز تظهر لادوريتها

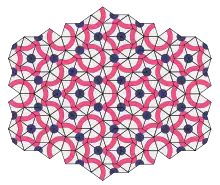
التبليط أو الفسيفساء في الفضاء الإقليدي هي إمكانية رص مجموعة من الأشكال مع بعضها لتغطي مساحة ما من دون أي فراغات ودون تشابك الأشكال مع بعضها. والتبليط الدوري هو استعمال أنواع من الأشكال التي تكرر نفسها أن رصت مع بعض. وعادة، هذه الأشكال تكون أشكال غير متغيرة ان تعرضت لانزلاق هندسي. مثلا، رص شكل المربع يشكل تبليط دوري. أمأ زمرة التبليط اللادوري، فهي تتألف من أشكال غير دورية[1][2]

مثال على هذه الفكرة هي تبليط بنروز الذي، باستعمال شكلين لادوريين، يمكن أن نشكل عدد لانهائي من الأشكال اللادورية.

يوجد في الطبيعة العديد من الأمثلة مثل اشباه البلورات والتي تتألف من أشكال لادورية والتي اكتشفت من قبل العالم داني شيختمان في 1984 الأ اننا لا نعلم الكثير عن ماهيتها.[3]

وصلات خارجية

(بالإنجليزية: [http://www.ics.uci.edu/~eppstein/junkyard/tiling.html هندسة ساحة السكراب)‏]
(بالإنجليزية: تبليطات لادورية)‏

مراجع

skahg, lhv[,vd (1995)، أشباه البلورات والهندسة، مطبعة جامعة كامبريدج، ISBN 0-521-57541-9.
غرونباون, Branko (1986)، التبليط والأنماط، W.H. Freeman & Company، ISBN 0-7167-1194-X.
شيختمان, دان؛ بليش, أ.؛ غراتياس, د،؛ كاهن, J.W. (1984)، "Metallic Phase with long-range orientational order and no translational symmetry"، Phys. Rev. Letters، 53: 1951–1953، doi:10.1103/PhysRevLett.53.1951.

بوابة رياضيات
بوابة هندسة رياضية

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[senechal-1] skahg, lhv[,vd (1995)، أشباه البلورات والهندسة، مطبعة جامعة كامبريدج، ISBN 0-521-57541-9.

[grunbaum_and_shephard-2] غرونباون, Branko (1986)، التبليط والأنماط، W.H. Freeman & Company، ISBN 0-7167-1194-X.

[schechtman-3] شيختمان, دان؛ بليش, أ.؛ غراتياس, د،؛ كاهن, J.W. (1984)، "Metallic Phase with long-range orientational order and no translational symmetry"، Phys. Rev. Letters، 53: 1951–1953، doi:10.1103/PhysRevLett.53.1951.