تقابل (دالة)

في الرياضيات، الدالة التقابلية (بالإنجليزية: Bijective Function)‏ أو ببساطة، التقابل، هي دالة رياضية من مجموعة X إلى مجموعة Y حيث كل عنصر y من المجموعة المستقر Y ،هناك سابق واحد فقط x من المجموعة المنطلق X حيث يكون : f(x) = y أي أن y هي صورة x بالدالة f.[1][2][3]

دالة تباينية ولكنها غير شمولية. إذن، هي ليست دالة تقابلية.
دالة تباينية ولكنها غير شمولية. إذن، هي ليست دالة تقابلية.  
دالة تباينية وشمولية في آن واحد. إذن، هي دالة تقابلية.
دالة تباينية وشمولية في آن واحد. إذن، هي دالة تقابلية.  
دالة غير تباينية ولكنها شمولية. إذن، هي ليست دالة تقابلية.
دالة غير تباينية ولكنها شمولية. إذن، هي ليست دالة تقابلية.  
دالة غير تباينية وغير شمولية. إذن، هي ليست دالة تقابلية.
دالة غير تباينية وغير شمولية. إذن، هي ليست دالة تقابلية.  
  لمعانٍ أخرى، طالع تقابل (توضيح).

تعريف

تكون الدالة f تقابلا إذا كانت رابطا واحد لواحد بين عناصر المجموعتين المنطلق والمستقر أي أنها دالة تباينية (العناصر في المستقر لا ترتبط بعنصرين مختلفين في المنطلق) وفي نفس الوقت شمولية (لجميع عناصر المستقر مقابل ترتبط فيه من المنطلق).

التقابل في الهندسة الوصفية

في الهندسة الوصفية العلاقة التقابلية بين شكلين هندسيين delta و'delta (الشكل-2) هو رابط إسقاطي، بحيث أن:

  • كل نقطة A من delta تقابلها نقطة واحدة 'A من 'delta والعكس بالعكس.
  • أزواج الخطوط المتقابلة a' a، التي تمر بنقاط متقابلة A'B' A B، تلتقي على نفس الخط u (يُسمى محور التقابل).
  • النقاط المتقابلةِ 'A A و'B B تكون مصطفة مع نفس النفطة U (تُسمى مركز التقابل)
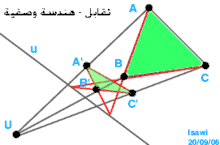
تقابل بين مثلثين 'ABC A'B'C صورة2. u: محور التقابل. U: مركز التقابل
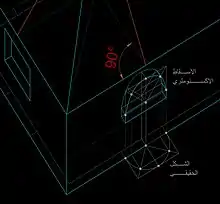
العلاقة التقابلية لتحديد فتحة قوسية على جدار رأسي في الاكسنومتري الكافاليرا الافقية (Plan oblique)

أمثلة
  • الدالة المحايدة هي دالة تقابلية.
  • الدالة التزايدية قطعا والمتصلة هي دالة تقابلية .
  • الدالة التناقصية قطعا والمتصلة هي دالة تقابلية .

الدوال العكسية

إذا كانت الدالة تقابلية فإنه سيكون لها دالة عكسية.

التركيب
دالة تقابلية مكونة من تركيب دالة تباينية (في اليسار) ودالة شمولية (في اليمين).

اختبار الخط الأفقى للدالة

إذا مر بالدالة خط مستقيم واحد على الأكثر فإن الدالة هي دالة تقايبلية .

مراجع
  1. Christopher Hollings (16 يوليو 2014)، Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups، American Mathematical Society، ص. 251، ISBN 978-1-4704-1493-1، مؤرشف من الأصل في 11 أبريل 2020.
  2. Pierre A. Grillet (1995)، Semigroups: An Introduction to the Structure Theory، CRC Press، ص. 228، ISBN 978-0-8247-9662-4، مؤرشف من الأصل في 17 مارس 2017.
  3. John Meakin (2007)، "Groups and semigroups: connections and contrasts"، Groups St Andrews 2005 Volume 2، Cambridge University Press، ص. 367، ISBN 978-0-521-69470-4.

انظر أيضًا
  • بوابة رياضيات
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.