متباينة ينسن
متراجحة ينسن في الرياضيات، والمنسوبة إلى عالم الرياضيات الدانيماركي يوهان ينسن، تربط ما بين قيمة تراكب دالة محدّبة على تكامل وبين قيمة تراكب التكامل على نفس الدالة المحدّبة. وقد قام ينسن ببرهان هذه المتراجحة في عام 1906.[1] كون المتراجحة قانونًا عامًا يؤدي إلى أن يصلح استخدامها في عدة سياقات وعدة أشكال. وبصيغتها الأكثر بساطة، تنص المتراجحة على أنّ «التحويل المحدّب لمتوسّط حسابي لمتغير أو قيم معينة أصغر من أو مساوٍ للمتوسّط الحسابي لذات التحويل المحدب لنفس المتغير أو القيم».
متباينة ينسن
|
نصوص
الصيغة المحدودة
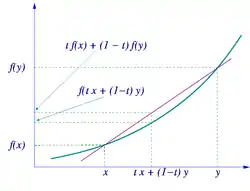
لأي دالة محدبة ، وأعداد في نطاق الدالة، وعوامل ترجيح موجبة ملائمة ، بالإمكان نص متراجحة ينسن كالتالي:
حيث أن المتراجحة تكون معكوسة إذا كانت الدالة مقعرة. وبشكل خاص، فإذا كانت جميع عوامل الترجيح متساوية، نحصل على المتراجحة الآتية:
- .
على سبيل المثال، إذا أخذنا الدالة ، وهي دالة مقعرة (إذ ) وتصاعدية، فبما أنّ المتراجحة الآتية صحيحة لكونها المتراجحة الشهيرة بين المتوسط الحسابي والمتوسط الهندسي لـn أعداد:
وبما أنّ تصاعدية:
أي أنّ متباينة ينسن تتحقّق لهذه الحالة. يشار إلى أنّ المتغيرات قد تكون دالة من متغير آخر t، بحيث . وبشكل عام أكثر، فبالإمكان النظر إلى الحالة المستمرّة، حيث تستبدل الجموع بتكاملات، وتستبدل عوامل الترجيح بدالة ترجيح غير سالبة، كدالة توزيع احتمالي، مثلاً.
الصيغة الاحتمالية
بالإمكان صياغ قانون مكافئ في سياق نظرية الاحتمالات. فإذا كان فضاء احتمالي، وكان متغيرًا عشوائيًا قابل للتكامل وذو قيم حقيقية وكانت الدالة دالة محدبة، فإنّ:
بحيث أنّ هي القيمة المتوقعة للمتغير .
انظر أيضًا
ملاحظات
- Jensen, J. L. W. V. (1906)، "Sur les fonctions convexes et les inégalités entre les valeurs moyennes"، Acta Mathematica، 30 (1): 175–193، doi:10.1007/BF02418571.
وصلات خارجية
- بوابة رياضيات
- بوابة تحليل رياضي