هرمية كثيرة الحدود

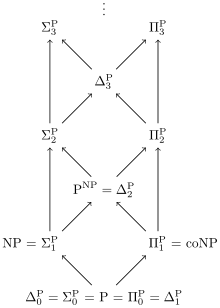
1. نعرف الاقسام التالية:

• ${\displaystyle \Sigma _{1}={\mbox{NP}}}$
• وبطريقة البناء عن طريق الاستقراء نعرف: ${\displaystyle \Sigma _{i}={\mbox{NP}}^{\Sigma _{i-1}}}$

في حين أنَّ:${\displaystyle {\mbox{NP}}^{C}}$ هي مجموعة اللغات التي يمكن تقريرها بواسطة آلة تيورنج كثيرة الحدود غير قطعية مع امكانية الدخول إلى اوراكل من القسم C .

حينها: ${\displaystyle {\mbox{PH}}=\cup _{i=0}^{\infty }\Sigma _{i}}$

2. نعرف القسم ${\displaystyle \Sigma _{i}}$ بشكل اخر:${\displaystyle {\mbox{L}}\in \Sigma _{i}}$ إذا يوجد علاقة محدودة بكثير حدود وقابلة للتمييز بوقت كثير الحدود مع i+1 متغيرات حيث أنَّ: ${\displaystyle x\in L\iff \exists y_{1}\forall y_{2}\cdots Q_{i}y_{i}(x,y_{1},y_{2},\cdots ,y_{i})\in R_{L}}$ في حين أنَّ

يمكن ان نبين أنَّ التعريفان متكافئان وذلك بواسطة الاستقراء لكل i .

على غرار co-NP , P يمكن تعريف اقسام مشابهة وهي:

• ${\displaystyle \Delta _{1}={\mbox{P}}}$
• ${\displaystyle \Delta _{i}={\mbox{P}}^{\Delta _{i-1}}}$
• ${\displaystyle \Pi _{1}={\mbox{co-NP}}}$
• ${\displaystyle \Pi _{i}={\mbox{co-NP}}^{\Pi _{i-1}}}$

ويمكن تعريف PH بواسطة ${\displaystyle \Delta _{i}}$ أو بواسطة ${\displaystyle \Pi _{i}}$ وذلك لانَّ:

• ${\displaystyle \Pi _{i}\subseteq \Sigma _{i+1}}$
• ${\displaystyle \Sigma _{i}\subseteq \Pi _{i+1}}$
• ${\displaystyle \Sigma _{i}\cup \Pi _{i}\subseteq \Delta _{i}\subseteq \Sigma _{i+1}\cap \Pi _{i+1}}$

نقول أنَّ PH انهارت إذا تحقق التالي:

يوجد k بحيث أنَّ ${\displaystyle \Sigma _{k}=\Sigma _{k+1}}$

حيث أنه إذا وجد k كهذا حينها: ${\displaystyle \Sigma _{k}={\mbox{PH}}}$ واغلب علماء الحاسوب والرياضيات يقولون بعدم انهيار الهرم كثير الحدود، ومع هذا فإنه غير معلوم إذا ما PH مُنهار أو لا !

• يمكن بسهولة تبيين أنَّ ${\displaystyle {\mbox{PH}}\subseteq {\mbox{PSPACE}}}$ . وذلك لاننا يمكننا تجربة كل الامكانيات كما في تعريف PH ونستخدم مساحة اضافية متعددة الحدود.
• إذا ${\displaystyle {\mbox{NP}}={\mbox{coNP}}}$ حينها ${\displaystyle {\mbox{PH=NP}}}$
• لكل i إذا ${\displaystyle \Sigma _{i}=\Pi _{i}}$ حينها ${\displaystyle {\mbox{PH}}=\Sigma _{i}}$
• مبرهنة سبسر ولوتومان: ${\displaystyle {\mbox{BPP}}\subseteq {\mbox{PH}}}$
• إذا ${\displaystyle {\mbox{NP}}\subseteq {\mbox{P/Poly}}}$ حينها: ${\displaystyle \Sigma _{2}=\Pi _{2}}$ أي انه ${\displaystyle {\mbox{PH}}=\Sigma _{2}}$ .
• مبرهنة كانان: لكل k، ${\displaystyle \Sigma _{2}}$ لا يتبع القسم: (Size(n^k
• مبرهنة تودا: ${\displaystyle {\mbox{PH}}\subseteq P^{\#P}}$

لكل Σ_i يمكن تعريف المسألة التالية: Σ_iSAT :

المعطى: صيغة ${\displaystyle \varphi ({\mbox{x,y}})}$ والتي هي بشكل SAT

المخرج: هل صحيح أنَّ: ${\displaystyle \exists x\forall y_{1}\exists y_{2}\cdots Q_{i}y_{i}\varphi ({\mbox{x}},{\mbox{y}}_{1},\cdots ,{\mbox{y}}_{i})}$ حيث أنَّ:

هذه المسألة كاملة ل-${\displaystyle \Sigma _{i}}$ . يمكن ايجاد مسائل أخرى كاملة [1] في الهامش.

لنفرض أن المسألة L هي كاملة في PH ، حينها يوجد k بحيث أنَّ ${\displaystyle {\mbox{L}}\in \Sigma _{k}}$ وبما أن هذه المسألة كاملة كل مسألة في PH يمكن اختزالها لهذه المسألة أي L ومن ضمن هذه المسائل نأخذ المسائل التي تتبع ${\displaystyle \Sigma _{k+1}}$ حينها كل مسألة كهذه تتبع أيضا ${\displaystyle \Sigma _{k}}$ وهذا يعني أنَّ ${\displaystyle \Sigma _{k+1}\subseteq \Sigma _{k}}$ وهذا يعني أنَّ ${\displaystyle PH=\Sigma _{k}}$ وهذا يعني أنَّ الهرم كثير الحدود ينهار ! لذا لا يمكن أن يكون هنالك مسائل كاملة الا إذا انهار PH . وهذا يعطي دليلا أنَّ PH و-PSPACE لا يمكن ان يكونا متساويتيين!

• قسم تعقيد
• نظرية التعقيد الحسابي.
• مسألة P=NP
• خوارزمية

• بوابة رياضيات
• بوابة علم الحاسوب