Bühlmann decompression algorithm

To calculate the minimum tolerable pressure ${\displaystyle P_{tol}}$, the constants ${\displaystyle a}$ and ${\displaystyle b}$, which are derived from the saturation half-time as follows (ZH-L 16 A):

${\displaystyle a={\frac {2\,{\text{atm}}}{\sqrt[{3}]{t_{1/2}}}}}$

${\displaystyle b=1.005-{\frac {1}{\sqrt[{2}]{t_{1/2}}}}}$

are used to calculate M-Value (${\displaystyle P_{tol}}$):

${\displaystyle P_{tol}=(P-a)\cdot b}$

The ${\displaystyle b}$ values calculated do not correspond to those used by Bühlmann for tissue compartments 4 (0.7825 instead of 0.7725) and 5 (0.8126 instead of 0.8125).[8]

Versions B and C have manually modified[8] the coefficient ${\displaystyle a}$.

The modified values of ${\displaystyle a}$ and ${\displaystyle b}$ are shown in bold in the table below.

According to Graham's Law, the speed of diffusion (or effusion) of two gases under the same conditions of temperature and pressure is inversely proportional to the square root of their molar mass (28.0184 g/mol for ${\displaystyle N_{2}}$ and 4.0026 g/mol for ${\displaystyle He}$, i.e. ${\displaystyle {\sqrt[{2}]{\frac {28.0184}{4.0026}}}=2.645}$), which means that ${\displaystyle He}$ molecules diffuse 2.645 times faster than ${\displaystyle N_{2}}$ molecules.

Bühlmann took this into account and divided all the tissue compartment half-time for air (nitrogen) by 2.645 to obtain a helium-specific set of parameters with the longest compartment set at ${\displaystyle {\frac {635}{2.645}}=240{\text{ mn.}}}$

The parameters of the M-Values (coefficients a and b) were determined specifically.

No model can manage the desaturation of two inert gases.

Some approaches only take into account the main inert gas (and ignore the other inert gas).

With Bühlmann,[9] a weighted average of the half-times and coefficients ${\displaystyle a}$ and ${\displaystyle b}$ is calculated as a function of the percentage of each inert gas to calculate a specific set of parameters.

Example :

Using a 18/50 trimix (18% ${\displaystyle O_{2}}$, 50% ${\displaystyle He}$, 32% ${\displaystyle N_{2}}$), the half-time (or the ${\displaystyle a}$ and ${\displaystyle b}$ coefficients) of compartment #1 is calculated by taking 50% of the ${\displaystyle He}$ half-time and 32% of the ${\displaystyle N_{2}}$ half-time divided by 50% + 32% = 82%.

Example, compartment #1:

${\displaystyle t_{1/2}({\text{tx }}18/50)={\frac {(1.51\times 0.5)+(4\times 0.32)}{0.50+0.32}}={\frac {(0.755+1.28)}{0.82}}=2.48}$ (instead of ${\displaystyle 1.51}$ with ${\displaystyle He}$ and ${\displaystyle 4}$ with ${\displaystyle N_{2}}$)

${\displaystyle a({\text{tx }}18/50)={\frac {(1.7474\times 0.5)+(1.2599\times 0.32)}{0.50+0.32}}={\frac {(0.8737+0.403)}{0.82}}=1.5569}$ (${\displaystyle 1.7474}$ with ${\displaystyle He}$ and ${\displaystyle 1.2599}$ with ${\displaystyle N_{2}}$)

${\displaystyle b({\text{tx }}18/50)={\frac {(0.4245\times 0.5)+(0.5050\times 0.32)}{0.50+0.32}}={\frac {(0.2122+0.1616)}{0.82}}=0.4559}$ (${\displaystyle 0.4245}$ with ${\displaystyle He}$ and ${\displaystyle 0.5050}$ with ${\displaystyle N_{2}}$)

The same calculations can be made using partial pressures rather than percentages.

This approach is controversial with some authors[10] who feel that this calculation does not reflect what should be achieved. Generally speaking, the fact that desaturation with two neutral gases is not modelled encourages caution. Each trimix dive is specific, with no guarantee.

There are no specific model for constant ${\displaystyle PpO_{2}}$ dives. The difference lies in the fact that, at all times, the proportion of inert gas is calculated in relation to the chosen ${\displaystyle PpO_{2}}$ (e.g. 0.75 or 1.3 ata (bar)).

Table of ZH-L 16 Half-times ${\displaystyle t_{1/2}}$ with ${\displaystyle a}$ and ${\displaystyle b}$ values for nitrogen (${\displaystyle N_{2}}$) and helium (${\displaystyle He}$).[8]

Cpt	ZH-L 16 ${\displaystyle N_{2}}$					ZH-L 16 A ${\displaystyle He}$
	${\displaystyle t_{1/2}}$ (min)	A Experimental	B Tables	C Computers	${\displaystyle b}$	${\displaystyle t_{1/2}}$ (min)	${\displaystyle a}$	${\displaystyle b}$
		${\displaystyle a}$	${\displaystyle a}$	${\displaystyle a}$
01 (1a)	004	1.2599	1.2599	1.2599	0.5050	001.51	1.7474	0.4245
01b	005	1.1696	1.1696	1.1696	0.5578	00
02	008	1.0000	1.0000	1.0000	0.6514	003.02	1.3830	0.5747
03	012.5	0.8618	0.8618	0.8618	0.7222	004.72	1.1919	0.6527
04	018.5	0.7562	0.7562	0.7562	0.7825	006.99	1.0458	0.7223
05	027	0.6667	0.6667	0.6200	0.8126	010.21	0.9220	0.7582
06	038.3	0.5933	0.5600	0.5043	0.8434	014.48	0.8205	0.7957
07	054.3	0.5282	0.4947	0.4410	0.8693	020.53	0.7305	0.8279
08	077	0.4701	0.4500	0.4000	0.8910	029.11	0.6502	0.8553
09	109	0.4187	0.4187	0.3750	0.9092	041.2	0.5950	0.8757
10	146	0.3798	0.3798	0.3500	0.9222	055.19	0.5545	0.8903
11	187	0.3497	0.3497	0.3295	0.9319	070.69	0.5333	0.8997
12	239	0.3223	0.3223	0.3065	0.9403	090.34	0.5189	0.9073
13	305	0.2971	0.2850	0.2835	0.9477	115.29	0.5181	0.9122
14	390	0.2737	0.2737	0.2610	0.9544	147.42	0.5176	0.9171
15	498	0.2523	0.2523	0.2480	0.9602	188.24	0.5172	0.9217
16	635	0.2327	0.2327	0.2327	0.9653	240.03	0.5119	0.9267

Several versions of the Bühlmann set of parameters have been developed, both by Bühlmann and by later workers. The naming convention used to identify the set of parameters is a code starting ZH-L, from Zürich (ZH), Linear (L) followed by the number of different (a,b) couples (ZH-L 12 and ZH-L 16)[11]) or the number of tissue compartments (ZH-L 6, ZH-L 8), and other unique identifiers. For example:

ZH-L 12 (1983)

• ZH-L 12: The set of parameters published in 1983 with "Twelve Pairs of Coefficients for Sixteen Half-Value Times"[11]

ZH-L 16 (1986)[12]

• ZH-L 16 or ZH-L 16 A (air, nitrox): The experimental set of parameters published in 1986.
• ZH-L 16 B (air, nitrox): The set of parameters modified for printed dive table production, using slightly more conservative “a” values for tissue compartments #6, 7, 8 and 13.
• ZH-L 16 C (air, nitrox): The set of parameters with more conservative “a” values for tissue compartments #5 to 15. For use in dive computers.
• ZH-L 16 (helium): The set of parameters for use with helium.
• ZH-L 16 ADT MB: set of parameters and specific algorithm used by Uwatec for their trimix-enabled computers. Modified in the middle compartments from the original ZHL-C, is adaptive to diver workload and includes Profile-Determined Intermediate Stops. Profile modification is by means of "MB Levels", personal option conservatism settings, which are not defined in the manual.[13]

ZH-L 6 (1988)

• ZH-L 6 is an adaptation[14] (Albert Bühlmann, Ernst B.Völlm and Markus Mock) of the ZH-L16 set of parameters, implemented in Aladin Pro computers (Uwatec, Beuchat), with 6 tissue compartments (half-time : 6 mn / 14 mn / 34 mn / 64 mn / 124 mn / 320 mn).

ZH-L 8 ADT (1992)

• ZH-L 8 ADT: A new approach with variable half-times and supersaturation tolerance depending on risk factors.[14] The set of parameters and the algorithm are not public (Uwatec property, implemented in Aladin Air-X in 1992 and presented at BOOT in 1994). This algorithm may reduce the no-stop limit or require the diver to complete a compensatory decompression stop after an ascent rate violation, high work level during the dive, or low water temperature. This algorithm may also take into account the specific nature of repetitive dives.

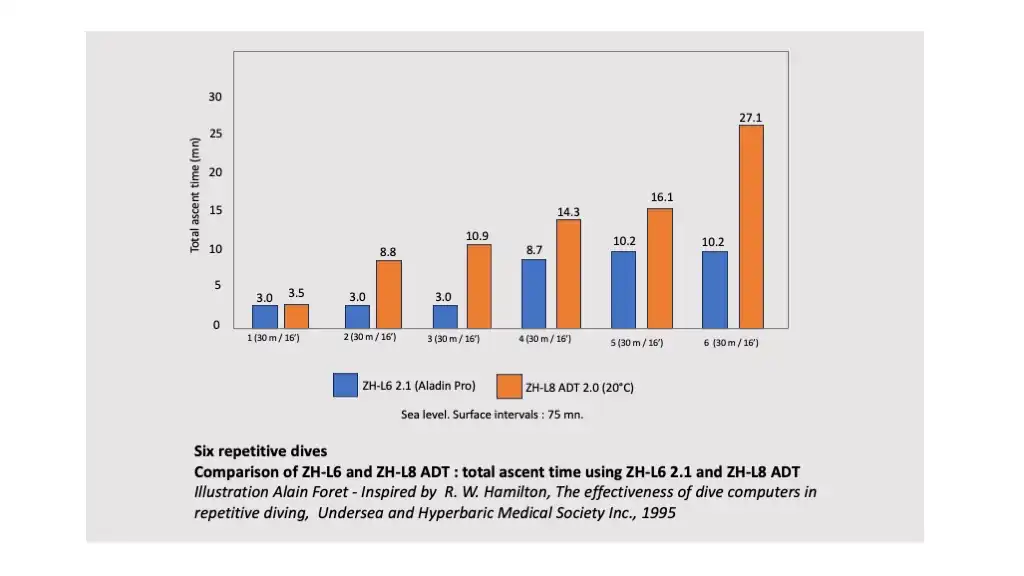
• ZH-L 8 ADT MB: A version of the ZHL-8 ADT claimed to suppress MicroBubble formation.[15]
• ZH-L 8 ADT MB PDIS: Profile-Determined Intermediate Stops.[16]
• ZH-L 8 ADT MB PMG: Predictive Multi-Gas.[17]