Hexahedron

A hexahedron (PL: hexahedra or hexahedrons) or sexahedron (PL: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.

There are seven topologically distinct convex hexahedra,[1] one of which exists in two mirror image forms. There are three topologically distinct concave hexahedra. Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.

Convex, Cuboid
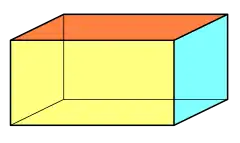
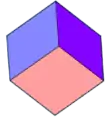
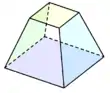
Quadrilaterally-faced hexahedron (Cuboid) 6 faces, 12 edges, 8 vertices
Cube
(square)		 Rectangular cuboid
(three pairs of
rectangles)		 Trigonal trapezohedron
(congruent rhombi)		 Trigonal trapezohedron
(congruent quadrilaterals)		 Quadrilateral frustum
(apex-truncated
square pyramid)		 Parallelepiped
(three pairs of
parallelograms)		 Rhombohedron
(three pairs of
rhombi)
Oh, [4,3], (*432)
order 48		 D2h, [2,2], (*222)
order 8		 D3d, [2+,6], (2*3)
order 12		 D3, [2,3]+, (223)
order 6		 C4v, [4], (*44)
order 8		 Ci, [2+,2+], (×)
order 2

Convex, Others
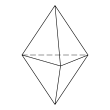
Convex
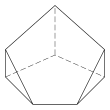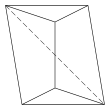
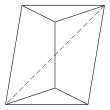
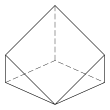
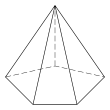
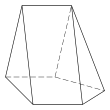
Triangular bipyramid Tetragonal antiwedge. Chiral – exists in "left-handed" and "right-handed" mirror image forms. Pentagonal pyramid
36 Faces
9 E, 5 V		 4.4.3.3.3.3 Faces
10 E, 6 V		 4.4.4.4.3.3 Faces
11 E, 7 V		 5.35 Faces
10 E, 6 V		 5.4.4.3.3.3 Faces
11 E, 7 V		 5.5.4.4.3.3 Faces
12 E, 8 V

Concave

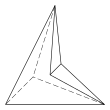
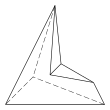
There are three further topologically distinct hexahedra that can only be realised as concave figures:

Concave
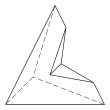4.4.3.3.3.3 Faces
10 E, 6 V		 5.5.3.3.3.3 Faces
11 E, 7 V		 6.6.3.3.3.3 Faces
12 E, 8 V

A digonal antiprism can be considered a degenerate form of hexahedron, having two opposing digonal faces and four triangular faces. However, digons are usually disregarded in the definition of non-spherical polyhedra, and this case is often simply considered a tetrahedron and the four remaining triangular faces considered to compose the full solid.

See also

References
  1. Counting polyhedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.