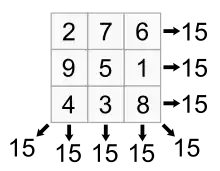
Magic polygon

A magic polygon is a polygonal magic graph with integers on its vertices.

Not to be confused with Polygon Magic.

Perimeter magic polygon

A magic polygon, also called a perimeter magic polygon,[1][2] is a polygon with an integers on its sides that all add up to a magic constant.[3][4] It is where positive integers (from 1 to N) on a k-sided polygon add up to a constant.[1] Magic polygons are a generalization of other magic shapes[5] such as magic triangles.[6]

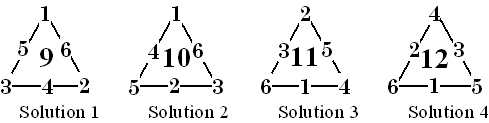
This displays order 3 magic triangles, a type of magic polygon.

Magic polygon with a center point

Victoria Jakicic and Rachelle Bouchat defined magic polygons as n-sided regular polygons with 2n+1 nodes such that the sum of the three nodes are equal. In their definition, a 3 × 3 magic square can be viewed as a magic 4-gon. There are no magic odd-gons with this definition.[7]

Magic polygons and degenerated magic polygons

Danniel Dias Augusto and Josimar da Silva defined the magic polygon P(n,k) as a set of vertices of concentric n-gon and a center point. In this definition, magic polygons of Victoria Jakicic and Rachelle Bouchat can be viewed as P(n,2) magic polygons. They also defined degenerated magic polygons.[8]

See also

References
  1. "Perimeter Maghic Polygons". www.trottermath.net. Archived from the original on 2018-01-12. Retrieved 2017-02-12.
  2. "Perimeter Magic Polygon >k=3". www.magic-squares.net. Retrieved 2017-02-12.
  3. Staszkow, Ronald (2003-05-01). Math Skills: Arithmetic with Introductory Algebra and Geometry. Kendall Hunt. p. 199. ISBN 9780787292966. Magic polygon math.
  4. Bolt, Brian (1987-04-09). Even More Mathematical Activities. Cambridge University Press. ISBN 9780521339940.
  5. Croft, Hallard T.; Falconer, Kenneth; Guy, Richard K. (2012-12-06). Unsolved Problems in Geometry: Unsolved Problems in Intuitive Mathematics. Springer Science & Business Media. ISBN 9781461209638.
  6. Heinz, Harvey D. "Perimeter Magic Triangles". recmath.org. Retrieved 2017-02-12.
  7. Jakicic, Victoria; Bouchat, Rachelle (2018). "Magic Polygons and Their Properties". arXiv:1801.02262 [math.CO].
  8. Danniel Dias Augusto; Josimar da Silva Rocha (2019). "Magic Polygons and Degenerated Magic Polygons: Characterization and Properties". arXiv:1906.11342 [math.CO].


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.