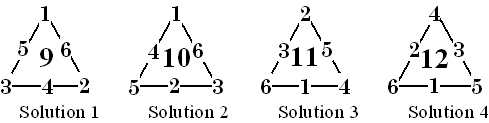Magic triangle (mathematics)

A magic triangle or perimeter magic triangle[1] is an arrangement of the integers from 1 to n on the sides of a triangle with the same number of integers on each side, called the order of the triangle, so that the sum of integers on each side is a constant, the magic sum of the triangle.[1][2][3][4] Unlike magic squares, there are different magic sums for magic triangles of the same order.[1] Any magic triangle has a complementary triangle obtained by replacing each integer x in the triangle with 1 + n − x.[1]

Examples

Order-3 magic triangles

Order-3 magic triangles are the simplest (except for trivial magic triangles of order 1).[1]

Other magic triangles use Triangular number or square number of vertices to form magic figure. Matthew Wright and his students in St. Olaf College developed magic triangles with square numbers. In their magic triangles, the sum of the k-th row and the (n-k+1)-th row is same for all k.[5] Its one modification uses triangular numbers instead of square nubers. (sequence A355119 in the OEIS) Another magic tringle form is magic triangles with triangluar numbers with different summation. In this magic triangles, the sum of the k-th row and the (n-k)-th row is same for all k. (sequence A356643 in the OEIS)

Magic Triangles have also been discovered, such that when its elements are squared, we obtain another magic triangle.

• Magic hexagon
• Antimagic square
• Magic polygon