Map of lattices
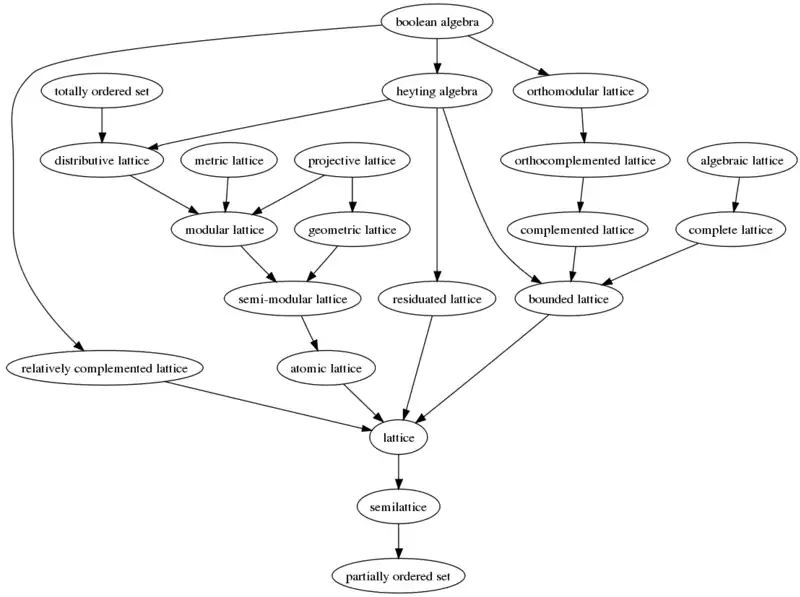
The concept of a lattice arises in order theory, a branch of mathematics. The Hasse diagram below depicts the inclusion relationships among some important subclasses of lattices.
Proofs of the relationships in the map
| Algebraic structures |
|---|
1. A boolean algebra is a complemented distributive lattice. (def)
2. A boolean algebra is a heyting algebra.[1]
3. A boolean algebra is orthocomplemented.[2]
4. A distributive orthocomplemented lattice is orthomodular.
5. A boolean algebra is orthomodular. (1,3,4)
6. An orthomodular lattice is orthocomplemented. (def)
7. An orthocomplemented lattice is complemented. (def)
8. A complemented lattice is bounded. (def)
9. An algebraic lattice is complete. (def)
10. A complete lattice is bounded.
11. A heyting algebra is bounded. (def)
12. A bounded lattice is a lattice. (def)
13. A heyting algebra is residuated.
14. A residuated lattice is a lattice. (def)
15. A distributive lattice is modular.[3]
16. A modular complemented lattice is relatively complemented.[4]
17. A boolean algebra is relatively complemented. (1,15,16)
18. A relatively complemented lattice is a lattice. (def)
19. A heyting algebra is distributive.[5]
20. A totally ordered set is a distributive lattice.
21. A metric lattice is modular.[6]
22. A modular lattice is semi-modular.[7]
23. A projective lattice is modular.[8]
24. A projective lattice is geometric. (def)
25. A geometric lattice is semi-modular.[9]
26. A semi-modular lattice is atomic.[10]
27. An atomic lattice is a lattice. (def)
28. A lattice is a semi-lattice. (def)
29. A semi-lattice is a partially ordered set. (def)
Notes
- Rutherford (1965), p.77.
- Rutherford (1965), p.32-33.
- Rutherford (1965), p.22.
- Rutherford (1965), p.31.
- Rutherford (1965), Th.25.1 p.74.
- Rutherford (1965), Th.8.1 p.22.
- Rutherford (1965), p.87.
- Rutherford (1965), p.94.
- Rutherford (1965), Th.32.1 p.92.
- Rutherford (1965), p.89.
References
- Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd.