Vector processor

Vector processing development began in the early 1960s at the Westinghouse Electric Corporation in their Solomon project. Solomon's goal was to dramatically increase math performance by using a large number of simple coprocessors under the control of a single master Central processing unit (CPU). The CPU fed a single common instruction to all of the arithmetic logic units (ALUs), one per cycle, but with a different data point for each one to work on. This allowed the Solomon machine to apply a single algorithm to a large data set, fed in the form of an array.

In 1962, Westinghouse cancelled the project, but the effort was restarted by the University of Illinois at Urbana–Champaign as the ILLIAC IV. Their version of the design originally called for a 1 GFLOPS machine with 256 ALUs, but, when it was finally delivered in 1972, it had only 64 ALUs and could reach only 100 to 150 MFLOPS. Nevertheless, it showed that the basic concept was sound, and, when used on data-intensive applications, such as computational fluid dynamics, the ILLIAC was the fastest machine in the world. The ILLIAC approach of using separate ALUs for each data element is not common to later designs, and is often referred to under a separate category, massively parallel computing. Around this time Flynn categorized this type of processing as an early form of single instruction, multiple threads (SIMT).

A computer for operations with functions was presented and developed by Kartsev in 1967.[1]

The first vector supercomputers are the Control Data Corporation STAR-100 and Texas Instruments Advanced Scientific Computer (ASC), which were introduced in 1974 and 1972, respectively.

The basic ASC (i.e., "one pipe") ALU used a pipeline architecture that supported both scalar and vector computations, with peak performance reaching approximately 20 MFLOPS, readily achieved when processing long vectors. Expanded ALU configurations supported "two pipes" or "four pipes" with a corresponding 2X or 4X performance gain. Memory bandwidth was sufficient to support these expanded modes.

The STAR-100 was otherwise slower than CDC's own supercomputers like the CDC 7600, but at data-related tasks they could keep up while being much smaller and less expensive. However the machine also took considerable time decoding the vector instructions and getting ready to run the process, so it required very specific data sets to work on before it actually sped anything up.

The vector technique was first fully exploited in 1976 by the famous Cray-1. Instead of leaving the data in memory like the STAR-100 and ASC, the Cray design had eight vector registers, which held sixty-four 64-bit words each. The vector instructions were applied between registers, which is much faster than talking to main memory. Whereas the STAR-100 would apply a single operation across a long vector in memory and then move on to the next operation, the Cray design would load a smaller section of the vector into registers and then apply as many operations as it could to that data, thereby avoiding many of the much slower memory access operations.

The Cray design used pipeline parallelism to implement vector instructions rather than multiple ALUs. In addition, the design had completely separate pipelines for different instructions, for example, addition/subtraction was implemented in different hardware than multiplication. This allowed a batch of vector instructions to be pipelined into each of the ALU subunits, a technique they called vector chaining. The Cray-1 normally had a performance of about 80 MFLOPS, but with up to three chains running it could peak at 240 MFLOPS and averaged around 150 – far faster than any machine of the era.

Cray J90 processor module with four scalar/vector processors

Other examples followed. Control Data Corporation tried to re-enter the high-end market again with its ETA-10 machine, but it sold poorly and they took that as an opportunity to leave the supercomputing field entirely. In the early and mid-1980s Japanese companies (Fujitsu, Hitachi and Nippon Electric Corporation (NEC) introduced register-based vector machines similar to the Cray-1, typically being slightly faster and much smaller. Oregon-based Floating Point Systems (FPS) built add-on array processors for minicomputers, later building their own minisupercomputers.

Throughout, Cray continued to be the performance leader, continually beating the competition with a series of machines that led to the Cray-2, Cray X-MP and Cray Y-MP. Since then, the supercomputer market has focused much more on massively parallel processing rather than better implementations of vector processors. However, recognising the benefits of vector processing, IBM developed Virtual Vector Architecture for use in supercomputers coupling several scalar processors to act as a vector processor.

Although vector supercomputers resembling the Cray-1 are less popular these days, NEC has continued to make this type of computer up to the present day with their SX series of computers. Most recently, the SX-Aurora TSUBASA places the processor and either 24 or 48 gigabytes of memory on an HBM 2 module within a card that physically resembles a graphics coprocessor, but instead of serving as a co-processor, it is the main computer with the PC-compatible computer into which it is plugged serving support functions.

Modern graphics processing units (GPUs) include an array of shader pipelines which may be driven by compute kernels, and can be considered vector processors (using a similar strategy for hiding memory latencies). As shown in Flynn's 1972 paper the key distinguishing factor of SIMT-based GPUs is that it has a single instruction decoder-broadcaster but that the cores receiving and executing that same instruction are otherwise reasonably normal: their own ALUs, their own register files, their own Load/Store units and their own independent L1 data caches. Thus although all cores simultaneously execute the exact same instruction in lock-step with each other they do so with completely different data from completely different memory locations. This is significantly more complex and involved than "Packed SIMD", which is strictly limited to execution of parallel pipelined arithmetic operations only. Although the exact internal details of today's commercial GPUs are proprietary secrets, the MIAOW[2] team was able to piece together anecdotal information sufficient to implement a subset of the AMDGPU architecture.[3]

Several modern CPU architectures are being designed as vector processors. The RISC-V vector extension follows similar principles as the early vector processors, and is being implemented in commercial products such as the Andes Technology AX45MPV.[4] There are also several open source vector processor architectures being developed, including ForwardCom and Libre-SOC.

SIMD instruction sets lack crucial features when compared to vector processor instruction sets. The most important of these is that vector processors, inherently by definition and design, have always been variable-length since their inception.

Whereas pure (fixed-width, no predication) SIMD is commonly mistakenly claimed to be "vectors" (because SIMD processes data which happens to be vectors), through close analysis and comparison of historic and modern ISAs, actual vector processors may be observed to have the following features that no SIMD ISA has:

• a way to set the vector length, such as the vsetvl instruction in RISCV RVV,[6] or the lvl instruction in NEC SX,[7] without restricting the length to a power of two or to a multiple of a fixed data width.
• Iteration and reduction over elements within vectors.

Predicated SIMD (part of Flynn's taxonomy) which is comprehensive individual element-level predicate masks on every vector instruction as is now available in ARM SVE2.[8] and AVX-512, almost qualifies as a vector processor. Predicated SIMD uses fixed-width SIMD ALUs but allows locally controlled (predicated) activation of units to provide the appearance of variable length vectors. Examples below help explain these categorical distinctions.

SIMD, because it uses fixed-width batch processing, is unable by design to cope with iteration and reduction. This is illustrated further with examples, below.

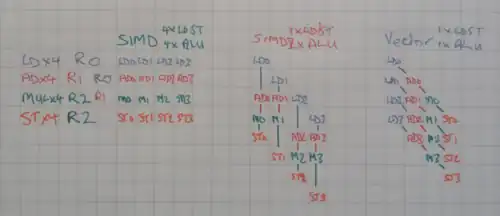
Additionally, vector processors can be more resource-efficient by using slower hardware and saving power, but still achieving throughput[9] and having less latency than SIMD, through vector chaining.[10]

Consider both a SIMD processor and a vector processor working on 4 64-bit elements, doing a LOAD, ADD, MULTIPLY and STORE sequence. If the SIMD width is 4, then the SIMD processor must LOAD four elements entirely before it can move on to the ADDs, must complete all the ADDs before it can move on to the MULTIPLYs, and likewise must complete all of the MULTIPLYs before it can start the STOREs. This is by definition and by design.[11]

Having to perform 4-wide simultaneous 64-bit LOADs and 64-bit STOREs is very costly in hardware (256 bit data paths to memory). Having 4x 64-bit ALUs, especially MULTIPLY, likewise. To avoid these high costs, a SIMD processor would have to have 1-wide 64-bit LOAD, 1-wide 64-bit STORE, and only 2-wide 64-bit ALUs. As shown in the diagram, which assumes a multi-issue execution model, the consequences are that the operations now take longer to complete. If multi-issue is not possible, then the operations take even longer because the LD may not be issued (started) at the same time as the first ADDs, and so on. If there are only 4-wide 64-bit SIMD ALUs, the completion time is even worse: only when all four LOADs have completed may the SIMD operations start, and only when all ALU operations have completed may the STOREs begin.

A vector processor, by contrast, even if it is single-issue and uses no SIMD ALUs, only having 1-wide 64-bit LOAD, 1-wide 64-bit STORE (and, as in the Cray-1, the ability to run MULTIPLY simultaneously with ADD), may complete the four operations faster than a SIMD processor with 1-wide LOAD, 1-wide STORE, and 2-wide SIMD. This more efficient resource utilization, due to vector chaining, is a key advantage and difference compared to SIMD. SIMD by design and definition cannot perform chaining except to the entire group of results.[12]

The vector pseudocode example above comes with a big assumption that the vector computer can process more than ten numbers in one batch. For a greater quantity of numbers in the vector register, it becomes unfeasible for the computer to have a register that large. As a result, the vector processor either gains the ability to perform loops itself, or exposes some sort of vector control (status) register to the programmer, usually known as a vector Length.

The self-repeating instructions are found in early vector computers like the STAR-100, where the above action would be described in a single instruction (somewhat like vadd c, a, b, $10). They are also found in the x86 architecture as the REP prefix. However, only very simple calculations can be done effectively in hardware this way without a very large cost increase. Since all operands have to be in memory for the STAR-100 architecture, the latency caused by access became huge too.

Interestingly, though, Broadcom included space in all vector operations of the Videocore IV ISA for a REP field, but unlike the STAR-100 which uses memory for its repeats, the Videocore IV repeats are on all operations including arithmetic vector operations. The repeat length can be a small range of power of two or sourced from one of the scalar registers.[15]

The Cray-1 introduced the idea of using processor registers to hold vector data in batches. The batch lengths (vector length, VL) could be dynamically set with a special instruction, the significance compared to Videocore IV (and, crucially as will be shown below, SIMD as well) being that the repeat length does not have to be part of the instruction encoding. This way, significantly more work can be done in each batch; the instruction encoding is much more elegant and compact as well. The only drawback is that in order to take full advantage of this extra batch processing capacity, the memory load and store speed correspondingly had to increase as well. This is sometimes claimed to be a disadvantage of Cray-style vector processors: in reality it is part of achieving high performance throughput, as seen in GPUs, which face exactly the same issue.

Modern SIMD computers claim to improve on early Cray by directly using multiple ALUs, for a higher degree of parallelism compared to only using the normal scalar pipeline. Modern vector processors (such as the SX-Aurora TSUBASA) combine both, by issuing multiple data to multiple internal pipelined SIMD ALUs, the number issued being dynamically chosen by the vector program at runtime. Masks can be used to selectively load and store data in memory locations, and use those same masks to selectively disable processing element of SIMD ALUs. Some processors with SIMD (AVX-512, ARM SVE2) are capable of this kind of selective, per-element ("predicated") processing, and it is these which somewhat deserve the nomenclature "vector processor" or at least deserve the claim of being capable of "vector processing". SIMD processors without per-element predication (MMX, SSE, AltiVec) categorically do not.

Modern GPUs, which have many small compute units each with their own independent SIMD ALUs, use Single Instruction Multiple Threads (SIMT). SIMT units run from a shared single broadcast synchronised Instruction Unit. The "vector registers" are very wide and the pipelines tend to be long. The "threading" part of SIMT involves the way data is handled independently on each of the compute units.

In addition, GPUs such as the Broadcom Videocore IV and other external vector processors like the NEC SX-Aurora TSUBASA may use fewer vector units than the width implies: instead of having 64 units for a 64-number-wide register, the hardware might instead do a pipelined loop over 16 units for a hybrid approach. The Broadcom Videocore IV is also capable of this hybrid approach: nominally stating that its SIMD QPU Engine supports 16-long FP array operations in its instructions, it actually does them 4 at a time, as (another) form of "threads".[16]

This example starts with an algorithm ("IAXPY"), first show it in scalar instructions, then SIMD, then predicated SIMD, and finally vector instructions. This incrementally helps illustrate the difference between a traditional vector processor and a modern SIMD one. The example starts with a 32-bit integer variant of the "DAXPY" function, in C:

void iaxpy(size_t n, int a, const int x[], int y[]) {
    for (size_t i = 0; i < n; i++)
        y[i] = a * x[i] + y[i];
}

In each iteration, every element of y has an element of x multiplied by a and added to it. The program is expressed in scalar linear form for readability.

The scalar version of this would load one of each of x and y, process one calculation, store one result, and loop:

loop:
  load32  r1, x      ; load one 32bit data
  load32  r2, y
  mul32   r1, a, r1  ; r1 := r1 * a
  add32   r3, r1, r2 ; r3 := r1 + r2
  store32 r3, y
  addl    x, x, $4   ; x := x + 4
  addl    y, y, $4
  subl    n, n, $1   ; n := n - 1
  jgz     n, loop    ; loop back if n > 0
out:
  ret

The STAR-like code remains concise, but because the STAR-100's vectorisation was by design based around memory accesses, an extra slot of memory is now required to process the information. Two times the latency is also needed due to the extra requirement of memory access.

  ; Assume tmp is pre-allocated
  vmul tmp, a, x, n ; tmp[i] = a * x[i]
  vadd y, y, tmp, n ; y[i] = y[i] + tmp[i]
  ret

A modern packed SIMD architecture, known by many names (listed in Flynn's taxonomy), can do most of the operation in batches. The code is mostly similar to the scalar version. It is assumed that both x and y are properly aligned here (only start on a multiple of 16) and that n is a multiple of 4, as otherwise some setup code would be needed to calculate a mask or to run a scalar version. It can also be assumed, for simplicity, that the SIMD instructions have an option to automatically repeat scalar operands, like ARM NEON can.[17] If it does not, a "splat" (broadcast) must be used, to copy the scalar argument across a SIMD register:

  splatx4   v4, a        ; v4 = a,a,a,a

The time taken would be basically the same as a vector implementation of y = mx + c described above.

vloop:
  load32x4  v1, x
  load32x4  v2, y
  mul32x4   v1, a, v1  ; v1 := v1 * a
  add32x4   v3, v1, v2 ; v3 := v1 + v2
  store32x4 v3, y
  addl      x, x, $16  ; x := x + 16
  addl      y, y, $16
  subl      n, n, $4   ; n := n - 4
  jgz       n, vloop   ; go back if n > 0
out:
  ret

Note that both x and y pointers are incremented by 16, because that is how long (in bytes) four 32-bit integers are. The decision was made that the algorithm shall only cope with 4-wide SIMD, therefore the constant is hard-coded into the program.

Unfortunately for SIMD, the clue was in the assumption above, "that n is a multiple of 4" as well as "aligned access", which, clearly, is a limited specialist use-case.

Realistically, for general-purpose loops such as in portable libraries, where n cannot be limited in this way, the overhead of setup and cleanup for SIMD in order to cope with non-multiples of the SIMD width, can far exceed the instruction count inside the loop itself. Assuming worst-case that the hardware cannot do misaligned SIMD memory accesses, a real-world algorithm will:

• first have to have a preparatory section which works on the beginning unaligned data, up to the first point where SIMD memory-aligned operations can take over. this will either involve (slower) scalar-only operations or smaller-sized packed SIMD operations. Each copy implements the full algorithm inner loop.
• perform the aligned SIMD loop at the maximum SIMD width up until the last few elements (those remaining that do not fit the fixed SIMD width)
• have a cleanup phase which, like the preparatory section, is just as large and just as complex.

Eight-wide SIMD requires repeating the inner loop algorithm first with four-wide SIMD elements, then two-wide SIMD, then one (scalar), with a test and branch in between each one, in order to cover the first and last remaining SIMD elements (0 <= n <= 7).

This more than triples the size of the code, in fact in extreme cases it results in an order of magnitude increase in instruction count! This can easily be demonstrated by compiling the iaxpy example for AVX-512, using the options "-O3 -march=knl" to gcc.

Over time as the ISA evolves to keep increasing performance, it results in ISA Architects adding 2-wide SIMD, then 4-wide SIMD, then 8-wide and upwards. It can therefore be seen why AVX-512 exists in x86.

Without predication, the wider the SIMD width the worse the problems get, leading to massive opcode proliferation, degraded performance, extra power consumption and unnecessary software complexity.[18]

Vector processors on the other hand are designed to issue computations of variable length for an arbitrary count, n, and thus require very little setup, and no cleanup. Even compared to those SIMD ISAs which have masks (but no setvl instruction), Vector processors produce much more compact code because they do not need to perform explicit mask calculation to cover the last few elements (illustrated below).

Assuming a hypothetical predicated (mask capable) SIMD ISA, and again assuming that the SIMD instructions can cope with misaligned data, the instruction loop would look like this:

vloop:
  # prepare mask. few ISAs have min though
  min       t0, n, $4     ; t0 = min(n, 4)
  shift     m, $1, t0     ; m = 1<<t0
  sub       m, m, $1      ; m = (1<<t0)-1
  # now do the operation, masked by m bits
  load32x4  v1, x, m
  load32x4  v2, y, m
  mul32x4   v1, a, v1, m  ; v1 := v1 * a
  add32x4   v3, v1, v2, m ; v3 := v1 + v2
  store32x4 v3, y, m
  # update x, y and n for next loop
  addl      x, t0*4      ; x := x + t0*4
  addl      y, t0*4
  subl      n, n, t0     ; n := n - t0
  # loop?
  jgz       n, vloop     ; go back if n > 0
out:
  ret

Here it can be seen that the code is much cleaner but a little complex: at least, however, there is no setup or cleanup: on the last iteration of the loop, the predicate mask wil be set to either 0b0000, 0b0001, 0b0011, 0b0111 or 0b1111, resulting in between 0 and 4 SIMD element operations being performed, respectively. One additional potential complication: some RISC ISAs do not have a "min" instruction, needing instead to use a branch or scalar predicated compare.

It is clear how predicated SIMD at least merits the term "vector capable", because it can cope with variable-length vectors by using predicate masks. The final evolving step to a "true" vector ISA, however, is to not have any evidence in the ISA at all of a SIMD width, leaving that entirely up to the hardware.

For Cray-style vector ISAs such as RVV, an instruction called "setvl" (set vector length) is used. The hardware first defines how many data values it can process in one "vector": this could be either actual registers or it could be an internal loop (the hybrid approach, mentioned above). This maximum amount (the number of hardware "lanes") is termed "MVL" (Maximum Vector Length). Note that, as seen in SX-Aurora and Videocore IV, MVL may be an actual hardware lane quantity or a virtual one. (Note: As mentioned in the ARM SVE2 Tutorial, programmers must not make the mistake of assuming a fixed vector width: consequently MVL is not a quantity that the programmer needs to know. This can be a little disconcerting after years of SIMD mindset).

On calling setvl with the number of outstanding data elements to be processed, "setvl" is permitted (essentially required) to limit that to the Maximum Vector Length (MVL) and thus returns the actual number that can be processed by the hardware in subsequent vector instructions, and sets the internal special register, "VL", to that same amount. ARM refers to this technique as "vector length agnostic" programming in its tutorials on SVE2.[19]

Below is the Cray-style vector assembler for the same SIMD style loop, above. Note that t0 (which, containing a convenient copy of VL, can vary) is used instead of hard-coded constants:

vloop:
  setvl   t0, n      # VL=t0=min(MVL, n)
  vld32   v0, x      # load vector x
  vld32   v1, y      # load vector y
  vmadd32 v1, v0, a  # v1 += v0 * a
  vst32   v1, y      # store Y
  add     y, t0*4    # advance y by VL*4
  add     x, t0*4    # advance x by VL*4
  sub     n, t0      # n -= VL (t0)
  bnez    n, vloop   # repeat if n != 0

This is essentially not very different from the SIMD version (processes 4 data elements per loop), or from the initial Scalar version (processes just the one). n still contains the number of data elements remaining to be processed, but t0 contains the copy of VL – the number that is going to be processed in each iteration. t0 is subtracted from n after each iteration, and if n is zero then all elements have been processed.

A number of things to note, when comparing against the Predicated SIMD assembly variant:

1. The setvl instruction has embedded within it a min instruction
2. Where the SIMD variant hard-coded both the width (4) into the creation of the mask and in the SIMD width (load32x4 etc.) the vector ISA equivalents have no such limit. This makes vector programs both portable, Vendor Independent, and future-proof.
3. Setting VL effectively creates a hidden predicate mask that is automatically applied to the vectors
4. Where with predicated SIMD the mask bitlength is limited to that which may be held in a scalar (or special mask) register, vector ISA's mask registers have no such limitation. Cray-I vectors could be just over 1,000 elements (in 1977).

Thus it can be seen, very clearly, how vector ISAs reduce the number of instructions.

Also note, that just like the predicated SIMD variant, the pointers to x and y are advanced by t0 times four because they both point to 32 bit data, but that n is decremented by straight t0. Compared to the fixed-size SIMD assembler there is very little apparent difference: x and y are advanced by hard-coded constant 16, n is decremented by a hard-coded 4, so initially it is hard to appreciate the significance. The difference comes in the realisation that the vector hardware could be capable of doing 4 simultaneous operations, or 64, or 10,000, it would be the exact same vector assembler for all of them and there would still be no SIMD cleanup code. Even compared to the predicate-capable SIMD, it is still more compact, clearer, more elegant and uses less resources.

Not only is it a much more compact program (saving on L1 Cache size), but as previously mentioned, the vector version can issue far more data processing to the ALUs, again saving power because Instruction Decode and Issue can sit idle.

Additionally, the number of elements going in to the function can start at zero. This sets the vector length to zero, which effectively disables all vector instructions, turning them into no-ops, at runtime. Thus, unlike non-predicated SIMD, even when there are no elements to process there is still no wasted cleanup code.

This example starts with an algorithm which involves reduction. Just as with the previous example, it will be first shown in scalar instructions, then SIMD, and finally vector instructions, starting in c:

void (size_t n, int a, const int x[]) {
    int y = 0;
    for (size_t i = 0; i < n; i++)
        y += x[i];
    return y;
}

Here, an accumulator (y) is used to sum up all the values in the array, x.

The scalar version of this would load each of x, add it to y, and loop:

  set     y, 0     ; y initialised to zero
loop:
  load32  r1, x    ; load one 32bit data
  add32   y, y, r1 ; y := y + r1
  addl    x, x, $4 ; x := x + 4
  subl    n, n, $1 ; n := n - 1
  jgz     n, loop  ; loop back if n > 0
out:
  ret y            ; returns result, y

This is very straightforward. "y" starts at zero, 32 bit integers are loaded one at a time into r1, added to y, and the address of the array "x" moved on to the next element in the array.

This is where the problems start. SIMD by design is incapable of doing arithmetic operations "inter-element". Element 0 of one SIMD register may be added to Element 0 of another register, but Element 0 may not be added to anything other than another Element 0. This places some severe limitations on potential implementations. For simplicity it can be assumed that n is exactly 8:

  addl      r3, x, $16 ; for 2nd 4 of x
  load32x4  v1, x      ; first 4 of x
  load32x4  v2, r3     ; 2nd 4 of x
  add32x4   v1, v2, v1 ; add 2 groups

At this point four adds have been performed:

• x[0]+x[4] - First SIMD ADD: element 0 of first group added to element 0 of second group
• x[1]+x[5] - Second SIMD ADD: element 1 of first group added to element 1 of second group
• x[2]+x[6] - Third SIMD ADD: element 2 of first group added to element 2 of second group
• x[3]+x[7] - Fourth SIMD ADD: element 3 of first group added to element 2 of second group

but with 4-wide SIMD being incapable by design of adding x[0]+x[1] for example, things go rapidly downhill just as they did with the general case of using SIMD for general-purpose IAXPY loops. To sum the four partial results, two-wide SIMD can be used, followed by a single scalar add, to finally produce the answer, but, frequently, the data must be transferred out of dedicated SIMD registers before the last scalar computation can be performed.

Even with a general loop (n not fixed), the only way to use 4-wide SIMD is to assume four separate "streams", each offset by four elements. Finally, the four partial results have to be summed. Other techniques involve shuffle: examples online can be found for AVX-512 of how to do "Horizontal Sum"[20][21]

Aside from the size of the program and the complexity, an additional potential problem arises if floating-point computation is involved: the fact that the values are not being summed in strict order (four partial results) could result in rounding errors.

Vector instruction sets have arithmetic reduction operations built-in to the ISA. If it is assumed that n is less or equal to the maximum vector length, only three instructions are required:

  setvl      t0, n  # VL=t0=min(MVL, n)
  vld32      v0, x  # load vector x
  vredadd32  y, v0  # reduce-add into y

The code when n is larger than the maximum vector length is not that much more complex, and is a similar pattern to the first example ("IAXPY").

  set     y, 0
vloop:
  setvl   t0, n      # VL=t0=min(MVL, n)
  vld32   v0, x      # load vector x
  vredadd32 y, y, v0 # add all x into y
  add     x, t0*4    # advance x by VL*4
  sub     n, t0      # n -= VL (t0)
  bnez    n, vloop   # repeat if n != 0
  ret y

The simplicity of the algorithm is stark in comparison to SIMD. Again, just as with the IAXPY example, the algorithm is length-agnostic (even on Embedded implementations where maximum vector length could be only one).

Implementations in hardware may, if they are certain that the right answer will be produced, perform the reduction in parallel. Some vector ISAs offer a parallel reduction mode as an explicit option, for when the programmer knows that any potential rounding errors do not matter, and low latency is critical.[22]

This example again highlights a key critical fundamental difference between true vector processors and those SIMD processors, including most commercial GPUs, which are inspired by features of vector processors.

Compared to any SIMD processor claiming to be a vector processor, the order of magnitude reduction in program size is almost shocking. However, this level of elegance at the ISA level has quite a high price tag at the hardware level:

1. From the IAXPY example, it can be seen that unlike SIMD processors, which can simplify their internal hardware by avoiding dealing with misaligned memory access, a vector processor cannot get away with such simplification: algorithms are written which inherently rely on Vector Load and Store being successful, regardless of alignment of the start of the vector.
2. Whilst from the reduction example it can be seen that, aside from permute instructions, SIMD by definition avoids inter-lane operations entirely (element 0 can only be added to another element 0), vector processors tackle this head-on. What programmers are forced to do in software (using shuffle and other tricks, to swap data into the right "lane") vector processors must do in hardware, automatically.

Overall then there is a choice to either have

1. complex software and simplified hardware (SIMD)
2. simplified software and complex hardware (vector processors)

These stark differences are what distinguishes a vector processor from one that has SIMD.

With many 3D shader applications needing trigonometric operations as well as short vectors for common operations (RGB, ARGB, XYZ, XYZW) support for the following is typically present in modern GPUs, in addition to those found in vector processors:

• Sub-vectors – elements may typically contain two, three or four sub-elements (vec2, vec3, vec4) where any given bit of a predicate mask applies to the whole vec2/3/4, not the elements in the sub-vector. Sub-vectors are also introduced in RISC-V RVV (termed "LMUL").[31] Subvectors are a critical integral part of the Vulkan SPIR-V spec.
• Sub-vector Swizzle – aka "Lane Shuffling" which allows sub-vector inter-element computations without needing extra (costly, wasteful) instructions to move the sub-elements into the correct SIMD "lanes" and also saves predicate mask bits. Effectively this is an in-flight mini-permute of the sub-vector, heavily features in 3D Shader binaries, and is sufficiently important as to be part of the Vulkan SPIR-V spec. The Broadcom Videocore IV uses the terminology "Lane rotate"[32] where the rest of the industry uses the term "swizzle".[33]
• Transcendentals – trigonometric operations such as sine, cosine and logarithm obviously feature much more predominantly in 3D than in many demanding HPC workloads. Of interest, however, is that speed is far more important than accuracy in 3D for GPUs, where computation of pixel coordinates simply do not require high precision. The Vulkan specification recognises this and sets surprisingly low accuracy requirements, so that GPU Hardware can reduce power usage. The concept of reducing accuracy where it is simply not needed is explored in the MIPS-3D extension.

Introduced in ARM SVE2 and RISC-V RVV is the concept of speculative sequential Vector Loads. ARM SVE2 has a special register named "First Fault Register",[34] where RVV modifies (truncates) the Vector Length (VL).[35]

The basic principle of ffirst is to attempt a large sequential Vector Load, but to allow the hardware to arbitrarily truncate the actual amount loaded to either the amount that would succeed without raising a memory fault or simply to an amount (greater than zero) that is most convenient. The important factor is that subsequent instructions are notified or may determine exactly how many Loads actually succeeded, using that quantity to only carry out work on the data that has actually been loaded.

Contrast this situation with SIMD, which is a fixed (inflexible) load width and fixed data processing width, unable to cope with loads that cross page boundaries, and even if they were they are unable to adapt to what actually succeeded, yet, paradoxically, if the SIMD program were to even attempt to find out in advance (in each inner loop, every time) what might optimally succeed, those instructions only serve to hinder performance because they would, by necessity, be part of the critical inner loop.

This begins to hint at the reason why ffirst is so innovative, and is best illustrated by memcpy or strcpy when implemented with standard 128-bit non-predicated non-ffirst SIMD. For IBM POWER9 the number of hand-optimised instructions to implement strncpy is in excess of 240.[36] By contrast, the same strncpy routine in hand-optimised RVV assembler is a mere 22 instructions.[37]

The above SIMD example could potentially fault and fail at the end of memory, due to attempts to read too many values: it could also cause significant numbers of page or misaligned faults by similarly crossing over boundaries. In contrast, by allowing the vector architecture the freedom to decide how many elements to load, the first part of a strncpy, if beginning initially on a sub-optimal memory boundary, may return just enough loads such that on subsequent iterations of the loop the batches of vectorised memory reads are optimally aligned with the underlying caches and virtual memory arrangements. Additionally, the hardware may choose to use the opportunity to end any given loop iteration's memory reads exactly on a page boundary (avoiding a costly second TLB lookup), with speculative execution preparing the next virtual memory page whilst data is still being processed in the current loop. All of this is determined by the hardware, not the program itself.[38]