Tangent half-angle substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of into an ordinary rational function of by setting . This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general[1] transformation formula is:
| Part of a series of articles about |
| Calculus |
|---|
The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent.[2] Leonhard Euler used it to evaluate the integral in his 1768 integral calculus textbook,[3] and Adrien-Marie Legendre described the general method in 1817.[4]
The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name.[5] It is known in Russia as the universal trigonometric substitution,[6] and also known by variant names such as half-tangent substitution or half-angle substitution. It is sometimes misattributed as the Weierstrass substitution.[7] Michael Spivak called it the "world's sneakiest substitution".[8]
The substitution
Introducing a new variable sines and cosines can be expressed as rational functions of and can be expressed as the product of and a rational function of as follows:
Derivation
Using the double-angle formulas, introducing denominators equal to one thanks to the Pythagorean theorem, and then dividing numerators and denominators by one gets
Finally, since , differentiation rules imply
and thus
Examples
Antiderivative of cosecant
We can confirm the above result using a standard method of evaluating the cosecant integral by multiplying the numerator and denominator by and performing the substitution .
These two answers are the same because
The secant integral may be evaluated in a similar manner.
A definite integral
In the first line, one cannot simply substitute for both limits of integration. The singularity (in this case, a vertical asymptote) of at must be taken into account. Alternatively, first evaluate the indefinite integral, then apply the boundary values.
By symmetry,
which is the same as the previous answer.
Third example: both sine and cosine
if
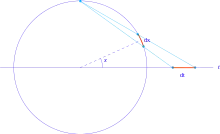
Geometry

As x varies, the point (cos x, sin x) winds repeatedly around the unit circle centered at (0, 0). The point
goes only once around the circle as t goes from −∞ to +∞, and never reaches the point (−1, 0), which is approached as a limit as t approaches ±∞. As t goes from −∞ to −1, the point determined by t goes through the part of the circle in the third quadrant, from (−1, 0) to (0, −1). As t goes from −1 to 0, the point follows the part of the circle in the fourth quadrant from (0, −1) to (1, 0). As t goes from 0 to 1, the point follows the part of the circle in the first quadrant from (1, 0) to (0, 1). Finally, as t goes from 1 to +∞, the point follows the part of the circle in the second quadrant from (0, 1) to (−1, 0).
Here is another geometric point of view. Draw the unit circle, and let P be the point (−1, 0). A line through P (except the vertical line) is determined by its slope. Furthermore, each of the lines (except the vertical line) intersects the unit circle in exactly two points, one of which is P. This determines a function from points on the unit circle to slopes. The trigonometric functions determine a function from angles to points on the unit circle, and by combining these two functions we have a function from angles to slopes.
Gallery
Hyperbolic functions
As with other properties shared between the trigonometric functions and the hyperbolic functions, it is possible to use hyperbolic identities to construct a similar form of the substitution, :
Geometrically, this change of variables is a one-dimensional analog of the Poincaré disk projection.
See also
Further reading
- Courant, Richard (1937) [1934]. "1.4.6. Integration of Some Other Classes of Functions §1–3". Differential and Integral Calculus. Vol. 1. Blackie & Son. pp. 234–237.
- Edwards, Joseph (1921). "§1.6.193". A Treatise on the Integral Calculus. Vol. 1. Macmillan. pp. 187–188.
- Hardy, Godfrey Harold (1905). "VI. Transcendental functions". The integration of functions of a single variable. Cambridge. pp. 42–51. Second edition 1916, pp. 52–62
- Hermite, Charles (1873). "Intégration des fonctions transcendentes" [Integration of transcendental functions]. Cours d'analyse de l'école polytechnique (in French). Vol. 1. Gauthier-Villars. pp. 320–380.
Notes and references
- Other trigonometric functions can be written in terms of sine and cosine.
- Gunter, Edmund (1673) [1624]. The Works of Edmund Gunter. Francis Eglesfield. p. 73
- Euler, Leonhard (1768). "§1.1.5.261 Problema 29" (PDF). Institutiones calculi integralis [Foundations of Integral Calculus] (in Latin). Vol. I. Impensis Academiae Imperialis Scientiarum. pp. 148–150. E342, Translation by Ian Bruce.
Also see Lobatto, Rehuel (1832). "19. Note sur l'intégration de la fonction ∂z / (a + b cos z)". Crelle's Journal (in French). 9: 259–260. - Legendre, Adrien-Marie (1817). Exercices de calcul intégral [Exercises in integral calculus] (in French). Vol. 2. Courcier. p. 245–246.
- For example, in chronological order,
- Hermite, Charles (1873). Cours d'analyse de l'école polytechnique (in French). Vol. 1. Gauthier-Villars. p. 320.
- Johnson, William Woolsey (1883). An Elementary Treatise on the Integral Calculus. MacMillan. p. 52.
- Picard, Émile (1901) [1891]. Traité d'analyse (in French). Vol. 1 (2e ed.). Gauthier-Villars. p. 77.
- Goursat, Édouard (1904) [1902]. A Course in Mathematical Analysis. Vol. 1. Translated by Hedrick, Earle Raymond. Ginn. pp. 236ff.
- Wilson, Edwin Bidwell (1911). Advanced Calculus. Ginn. p. 21.
- Edwards, Joseph (1921). A Treatise on the Integral Calculus. Vol. 1. MacMillan. pp. 187–188.
- Courant, Richard (1937) [1930]. Differential and Integral Calculus. Vol. 1. Translated by McShane, E. J. (2nd ed.). Blackie & Son. pp. 234–238.
- Peterson, Thurman S. (1950). Elements of Calculus. Harper & Brothers. pp. 201–202.
- Apostol, Tom M. (1967) [1961]. Calculus. Vol. 1 (2nd ed.). Xerox. pp. 264–265.
- Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (1998) [1978]. Calculus of a Single Variable (6th ed.). Houghton Mifflin. p. 520.
- Rogawski, Jon (2011) [2008]. Calculus: Early Transcendentals (2nd ed.). Macmillan. p. 435.
- Piskunov, Nikolai (1969). Differential and Integral Calculus. Mir. p. 379
-
William Eberlein attributed this substitution to Karl Weierstrass in 1966:
Eberlein, William Frederick (1966). "The Circular Function(s)". Mathematics Magazine. 39 (4): 197–201. doi:10.1080/0025570X.1966.11975715. JSTOR 2688079.
(Equations (3) [], (4) [], (5) [] are, of course, the familiar half-angle substitutions introduced by Weierstrass to integrate rational functions of sine, cosine.)
Two decades later, James Stewart mentioned Weirstrass when discussing the substitution in his popular calculus textbook, first published in 1987: Stewart, James (1987). "§7.5 Rationalizing substitutions". Calculus. Brooks/Cole. p. 431.The German mathematician Karl Weierstrauss (1815–1897) noticed that the substitution t = tan(x/2) will convert any rational function of sin x and cos x into an ordinary rational function.
Later authors, citing Stewart, have sometimes referred to this as the Weierstrass substitution, for instance:Neither Eberlein nor Stewart provided any evidence for the attribution to Weierstrass. A related substitution appears in Weierstrass’s Mathematical Works, from an 1875 lecture wherein Weierstrass credits Carl Gauss (1818) with the idea of solving an integral of the form by the substitution Weierstrass, Karl (1915) [1875]. "8. Bestimmung des Integrals ...". Mathematische Werke von Karl Weierstrass (in German). Vol. 6. Mayer & Müller. pp. 89–99.- Jeffrey, David J.; Rich, Albert D. (1994). "The evaluation of trigonometric integrals avoiding spurious discontinuities". Transactions on Mathematical Software. 20 (1): 124–135. doi:10.1145/174603.174409. S2CID 13891212.
- Merlet, Jean-Pierre (2004). "A Note on the History of Trigonometric Functions" (PDF). In Ceccarelli, Marco (ed.). International Symposium on History of Machines and Mechanisms. Kluwer. pp. 195–200. doi:10.1007/1-4020-2204-2_16. ISBN 978-1-4020-2203-6.
- Weisstein, Eric W. (2011). "Weierstrass Substitution". MathWorld. Retrieved 2020-04-01.
- Spivak, Michael (1967). "Ch. 9, problems 9–10". Calculus. Benjamin. pp. 325–326.