Crystal field theory
Crystal field theory (CFT) describes the breaking of degeneracies of electron orbital states, usually d or f orbitals, due to a static electric field produced by a surrounding charge distribution (anion neighbors). This theory has been used to describe various spectroscopies of transition metal coordination complexes, in particular optical spectra (colors). CFT successfully accounts for some magnetic properties, colors, hydration enthalpies, and spinel structures of transition metal complexes, but it does not attempt to describe bonding. CFT was developed by physicists Hans Bethe[1] and John Hasbrouck van Vleck[2] in the 1930s. CFT was subsequently combined with molecular orbital theory to form the more realistic and complex ligand field theory (LFT), which delivers insight into the process of chemical bonding in transition metal complexes.
Overview of crystal field theory
According to crystal field theory, the interaction between a transition metal and ligands arises from the attraction between the positively charged metal cation and the negative charge on the non-bonding electrons of the ligand. The theory is developed by considering energy changes of the five degenerate d-orbitals upon being surrounded by an array of point charges consisting of the ligands. As a ligand approaches the metal ion, the electrons from the ligand will be closer to some of the d-orbitals and farther away from others, causing a loss of degeneracy. The electrons in the d-orbitals and those in the ligand repel each other due to repulsion between like charges. Thus the d-electrons closer to the ligands will have a higher energy than those further away which results in the d-orbitals splitting in energy. This splitting is affected by the following factors:
- the nature of the metal ion.
- the metal's oxidation state. A higher oxidation state leads to a larger splitting relative to the spherical field.
- the arrangement of the ligands around the metal ion.
- the coordination number of the metal (i.e. tetrahedral, octahedral...)
- the nature of the ligands surrounding the metal ion. The stronger the effect of the ligands then the greater the difference between the high and low energy d groups.
The most common type of complex is octahedral, in which six ligands form the vertices of an octahedron around the metal ion. In octahedral symmetry the d-orbitals split into two sets with an energy difference, Δoct (the crystal-field splitting parameter, also commonly denoted by 10Dq for ten times the "differential of quanta"[3][4]) where the dxy, dxz and dyz orbitals will be lower in energy than the dz2 and dx2-y2, which will have higher energy, because the former group is farther from the ligands than the latter and therefore experiences less repulsion. The three lower-energy orbitals are collectively referred to as t2g, and the two higher-energy orbitals as eg. These labels are based on the theory of molecular symmetry: they are the names of irreducible representations of the octahedral point group, Oh.(see the Oh character table) Typical orbital energy diagrams are given below in the section High-spin and low-spin.
Tetrahedral complexes are the second most common type; here four ligands form a tetrahedron around the metal ion. In a tetrahedral crystal field splitting, the d-orbitals again split into two groups, with an energy difference of Δtet. The lower energy orbitals will be dz2 and dx2-y2, and the higher energy orbitals will be dxy, dxz and dyz - opposite to the octahedral case. Furthermore, since the ligand electrons in tetrahedral symmetry are not oriented directly towards the d-orbitals, the energy splitting will be lower than in the octahedral case. Square planar and other complex geometries can also be described by CFT.
The size of the gap Δ between the two or more sets of orbitals depends on several factors, including the ligands and geometry of the complex. Some ligands always produce a small value of Δ, while others always give a large splitting. The reasons behind this can be explained by ligand field theory. The spectrochemical series is an empirically-derived list of ligands ordered by the size of the splitting Δ that they produce (small Δ to large Δ; see also this table):
I− < Br− < S2− < SCN− (S–bonded) < Cl− < NO3− < N3− < F− < OH− < C2O42− < H2O < NCS− (N–bonded) < CH3CN < py < NH3 < en < 2,2'-bipyridine < phen < NO2− < PPh3 < CN− < CO.
It is useful to note that the ligands producing the most splitting are those that can engage in metal to ligand back-bonding.
The oxidation state of the metal also contributes to the size of Δ between the high and low energy levels. As the oxidation state increases for a given metal, the magnitude of Δ increases. A V3+ complex will have a larger Δ than a V2+ complex for a given set of ligands, as the difference in charge density allows the ligands to be closer to a V3+ ion than to a V2+ ion. The smaller distance between the ligand and the metal ion results in a larger Δ, because the ligand and metal electrons are closer together and therefore repel more.
High-spin and low-spin
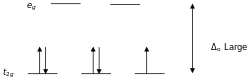
Ligands which cause a large splitting Δ of the d-orbitals are referred to as strong-field ligands, such as CN− and CO from the spectrochemical series. In complexes with these ligands, it is unfavourable to put electrons into the high energy orbitals. Therefore, the lower energy orbitals are completely filled before population of the upper sets starts according to the Aufbau principle. Complexes such as this are called "low spin". For example, NO2− is a strong-field ligand and produces a large Δ. The octahedral ion [Fe(NO2)6]3−, which has 5 d-electrons, would have the octahedral splitting diagram shown at right with all five electrons in the t2g level. This low spin state therefore does not follow Hund's rule.
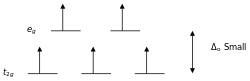
Conversely, ligands (like I− and Br−) which cause a small splitting Δ of the d-orbitals are referred to as weak-field ligands. In this case, it is easier to put electrons into the higher energy set of orbitals than it is to put two into the same low-energy orbital, because two electrons in the same orbital repel each other. So, one electron is put into each of the five d-orbitals in accord with Hund's rule, and "high spin" complexes are formed before any pairing occurs. For example, Br− is a weak-field ligand and produces a small Δoct. So, the ion [FeBr6]3−, again with five d-electrons, would have an octahedral splitting diagram where all five orbitals are singly occupied.
In order for low spin splitting to occur, the energy cost of placing an electron into an already singly occupied orbital must be less than the cost of placing the additional electron into an eg orbital at an energy cost of Δ. As noted above, eg refers to the dz2 and dx2-y2 which are higher in energy than the t2g in octahedral complexes. If the energy required to pair two electrons is greater than Δ, the energy cost of placing an electron in an eg, high spin splitting occurs.
The crystal field splitting energy for tetrahedral metal complexes (four ligands) is referred to as Δtet, and is roughly equal to 4/9Δoct (for the same metal and same ligands). Therefore, the energy required to pair two electrons is typically higher than the energy required for placing electrons in the higher energy orbitals. Thus, tetrahedral complexes are usually high-spin.
The use of these splitting diagrams can aid in the prediction of magnetic properties of co-ordination compounds. A compound that has unpaired electrons in its splitting diagram will be paramagnetic and will be attracted by magnetic fields, while a compound that lacks unpaired electrons in its splitting diagram will be diamagnetic and will be weakly repelled by a magnetic field.
Crystal field stabilization energy
The crystal field stabilization energy (CFSE) is the stability that results from placing a transition metal ion in the crystal field generated by a set of ligands. It arises due to the fact that when the d-orbitals are split in a ligand field (as described above), some of them become lower in energy than before with respect to a spherical field known as the barycenter in which all five d-orbitals are degenerate. For example, in an octahedral case, the t2g set becomes lower in energy than the orbitals in the barycenter. As a result of this, if there are any electrons occupying these orbitals, the metal ion is more stable in the ligand field relative to the barycenter by an amount known as the CFSE. Conversely, the eg orbitals (in the octahedral case) are higher in energy than in the barycenter, so putting electrons in these reduces the amount of CFSE.
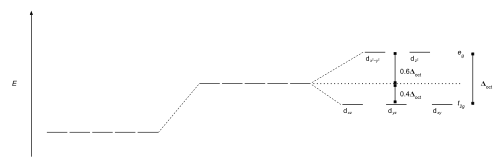
If the splitting of the d-orbitals in an octahedral field is Δoct, the three t2g orbitals are stabilized relative to the barycenter by 2/5 Δoct, and the eg orbitals are destabilized by 3/5 Δoct. As examples, consider the two d5 configurations shown further up the page. The low-spin (top) example has five electrons in the t2g orbitals, so the total CFSE is 5 x 2/5 Δoct = 2Δoct. In the high-spin (lower) example, the CFSE is (3 x 2/5 Δoct) - (2 x 3/5 Δoct) = 0 - in this case, the stabilization generated by the electrons in the lower orbitals is canceled out by the destabilizing effect of the electrons in the upper orbitals.
Optical properties
The optical properties (details of absorption and emission spectra) of many coordination complexes can be explained by Crystal Field Theory. Often, however, the deeper colors of metal complexes arise from more intense charge-transfer excitations.[5]
Geometries and crystal field splitting diagrams
| Name | Shape | Energy diagram |
|---|---|---|
| Octahedral |  | 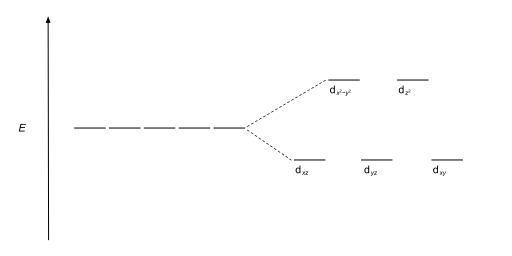 |
| Pentagonal bipyramidal |  |  |
| Square antiprismatic |  | 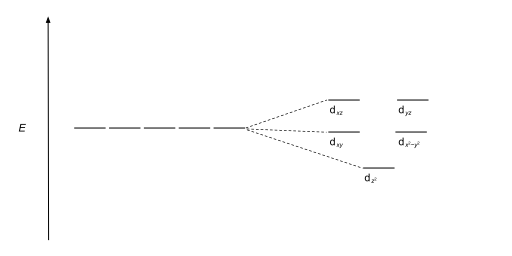 |
| Square planar | 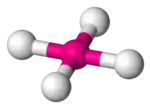 | 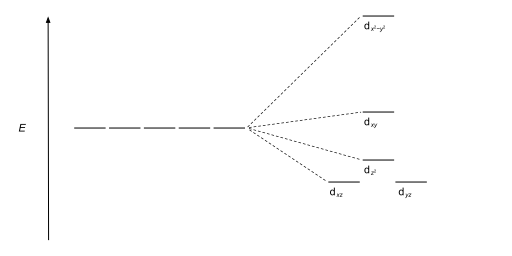 |
| Square pyramidal | 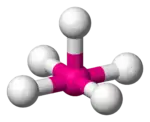 | 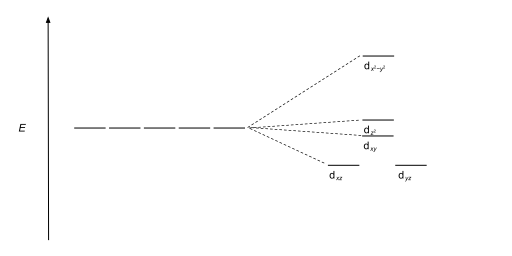 |
| Tetrahedral | 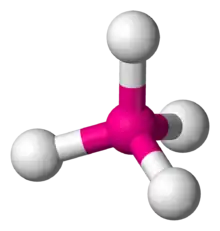 | 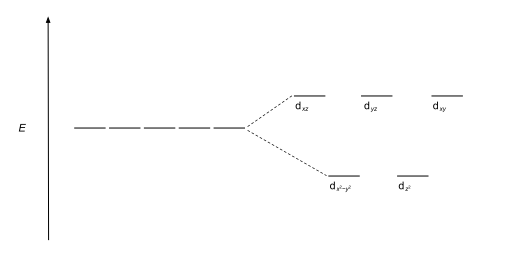 |
| Trigonal bipyramidal | 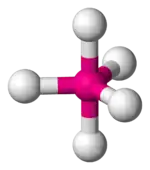 | 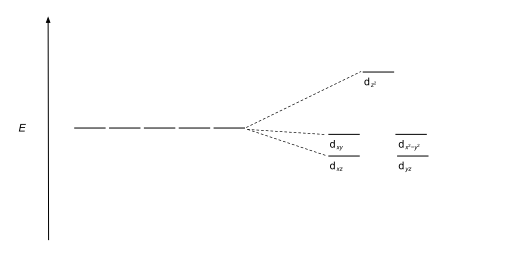 |
See also
- Schottky anomaly — low temperature spike in heat capacity seen in materials containing high-spin magnetic impurities, often due to crystal field splitting
- Ligand field theory
- Molecular orbital theory
References
- Bethe, H. (1929). "Termaufspaltung in Kristallen". Annalen der Physik (in German). 395 (2): 133–208. Bibcode:1929AnP...395..133B. doi:10.1002/andp.19293950202. ISSN 1521-3889.
- Van Vleck, J. (1932). "Theory of the Variations in Paramagnetic Anisotropy Among Different Salts of the Iron Group". Physical Review. 41 (2): 208–215. Bibcode:1932PhRv...41..208V. doi:10.1103/PhysRev.41.208.
- Penney, William G.; Schlapp, Robert (1932). "The Influence of Crystalline Fields on the Susceptibilities of Salts of Paramagnetic Ions. I. The Rare Earths, Especially Pr and Nd". Physical Review. 41 (2): 194–207. Bibcode:1932PhRv...41..194P. doi:10.1103/PhysRev.41.194. ISSN 0031-899X.
- Schlapp, Robert; Penney, William G. (1932). "Influence of Crystalline Fields on the Susceptibilities of Salts of Paramagnetic Ions. II. The Iron Group, Especially Ni, Cr and Co". Physical Review. 42 (5): 666–686. Bibcode:1932PhRv...42..666S. doi:10.1103/PhysRev.42.666. ISSN 0031-899X.\
- G. L. Miessler and D. A. Tarr “Inorganic Chemistry” 2nd Ed. (Prentice Hall 1999), p.379 ISBN 0-13-841891-8.
Further reading
- Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. ISBN 978-0-13-039913-7.
- Miessler, G. L.; Tarr, D. A. (2003). Inorganic Chemistry (3rd ed.). Pearson Prentice Hall. ISBN 978-0-13-035471-6.
- Orgel, Leslie E. (1960). An introduction to transition-metal chemistry: Ligand-Field theory. Methuen. ISBN 978-0416634402.
- Shriver, D. F.; Atkins, P. W. (2001). Inorganic Chemistry (4th ed.). Oxford University Press. pp. 227–236. ISBN 978-0-8412-3849-7.
- Silberberg, Martin S (2006). Chemistry: The Molecular Nature of Matter and Change (4th ed.). New York: McGraw Hill Company. pp. 1028–1034. ISBN 978-0-8151-8505-5.
- Zumdahl, Steven S (2005). Chemical Principles (5th ed.). Houghton Mifflin Company. pp. 550–551, 957–964. ISBN 978-0-669-39321-7.
External links
- Crystal-field Theory, Tight-binding Method, and Jahn-Teller Effect in E. Pavarini, E. Koch, F. Anders, and M. Jarrell (eds.): Correlated Electrons: From Models to Materials, Jülich 2012, ISBN 978-3-89336-796-2
- Crystal field theory (draft article) on Citizendium.org