Rayleigh distribution
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (/ˈreɪli/).[1]
|
Probability density function 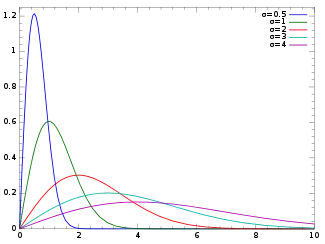 | |||
|
Cumulative distribution function 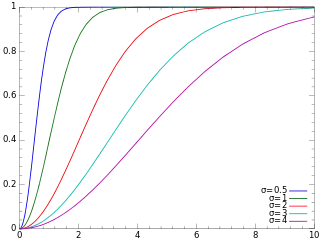 | |||
| Parameters | scale: | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
A Rayleigh distribution is often observed when the overall magnitude of a vector is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind velocity is analyzed in two dimensions. Assuming that each component is uncorrelated, normally distributed with equal variance, and zero mean, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are independently and identically distributed Gaussian with equal variance and zero mean. In that case, the absolute value of the complex number is Rayleigh-distributed.
Definition
The probability density function of the Rayleigh distribution is[2]
where is the scale parameter of the distribution. The cumulative distribution function is[2]
for
Relation to random vector length
Consider the two-dimensional vector which has components that are bivariate normally distributed, centered at zero, and independent. Then and have density functions
Let be the length of . That is, Then has cumulative distribution function
where is the disk
Writing the double integral in polar coordinates, it becomes
Finally, the probability density function for is the derivative of its cumulative distribution function, which by the fundamental theorem of calculus is
which is the Rayleigh distribution. It is straightforward to generalize to vectors of dimension other than 2. There are also generalizations when the components have unequal variance or correlations (Hoyt distribution), or when the vector Y follows a bivariate Student t-distribution (see also: Hotelling's T-squared distribution).[3]
Generalization to bivariate Student's t-distribution |
|---|
|
Suppose is a random vector with components that follows a multivariate t-distribution. If the components both have mean zero, equal variance, and are independent, the bivariate Student's-t distribution takes the form: Let be the magnitude of . Then the cumulative distribution function (CDF) of the magnitude is: where is the disk defined by: Converting to polar coordinates leads to the CDF becoming: Finally, the probability density function (PDF) of the magnitude may be derived: In the limit as , the Rayleigh distribution is recovered because: |
Properties
The raw moments are given by:
where is the gamma function.
The mean of a Rayleigh random variable is thus :
The standard deviation of a Rayleigh random variable is:
The variance of a Rayleigh random variable is :
The mode is and the maximum pdf is
The skewness is given by:
The excess kurtosis is given by:
The characteristic function is given by:
where is the imaginary error function. The moment generating function is given by
where is the error function.
Differential entropy
The differential entropy is given by
where is the Euler–Mascheroni constant.
Parameter estimation
Given a sample of N independent and identically distributed Rayleigh random variables with parameter ,
- is the maximum likelihood estimate and also is unbiased.
- is a biased estimator that can be corrected via the formula
Confidence intervals
To find the (1 − α) confidence interval, first find the bounds where:
then the scale parameter will fall within the bounds
Generating random variates
Given a random variate U drawn from the uniform distribution in the interval (0, 1), then the variate
has a Rayleigh distribution with parameter . This is obtained by applying the inverse transform sampling-method.
Related distributions
- is Rayleigh distributed if , where and are independent normal random variables.[6] This gives motivation to the use of the symbol in the above parametrization of the Rayleigh density.
- The magnitude of a standard complex normally distributed variable z is Rayleigh distributed.
- The chi distribution with v = 2 is equivalent to the Rayleigh Distribution with σ = 1.
- If , then has a chi-squared distribution with parameter , degrees of freedom, equal to two (N = 2)
- If , then has a gamma distribution with parameters and
- The Rice distribution is a noncentral generalization of the Rayleigh distribution: .
- The Weibull distribution with the shape parameter k=2 yields a Rayleigh distribution. Then the Rayleigh distribution parameter is related to the Weibull scale parameter according to
- The Maxwell–Boltzmann distribution describes the magnitude of a normal vector in three dimensions.
- If has an exponential distribution , then
- The half-normal distribution is the univariate special case of the Rayleigh distribution.
Applications
An application of the estimation of σ can be found in magnetic resonance imaging (MRI). As MRI images are recorded as complex images but most often viewed as magnitude images, the background data is Rayleigh distributed. Hence, the above formula can be used to estimate the noise variance in an MRI image from background data.[7] [8]
The Rayleigh distribution was also employed in the field of nutrition for linking dietary nutrient levels and human and animal responses. In this way, the parameter σ may be used to calculate nutrient response relationship.[9]
In the field of ballistics, the Rayleigh distribution is used for calculating the circular error probable - a measure of a weapon's precision.
In physical oceanography, the distribution of significant wave height approximately follows a Rayleigh distribution.[10]
See also
- Circular error probable
- Rayleigh fading
- Rayleigh mixture distribution
- Rice distribution
References
- "The Wave Theory of Light", Encyclopedic Britannica 1888; "The Problem of the Random Walk", Nature 1905 vol.72 p.318
- Papoulis, Athanasios; Pillai, S. (2001) Probability, Random Variables and Stochastic Processes. ISBN 0073660116, ISBN 9780073660110
- Röver, C. (2011). "Student-t based filter for robust signal detection". Physical Review D. 84 (12): 122004. arXiv:1109.0442. Bibcode:2011PhRvD..84l2004R. doi:10.1103/physrevd.84.122004.
- Siddiqui, M. M. (1964) "Statistical inference for Rayleigh distributions", The Journal of Research of the National Bureau of Standards, Sec. D: Radio Science, Vol. 68D, No. 9, p. 1007
- Siddiqui, M. M. (1961) "Some Problems Connected With Rayleigh Distributions", The Journal of Research of the National Bureau of Standards; Sec. D: Radio Propagation, Vol. 66D, No. 2, p. 169
- Hogema, Jeroen (2005) "Shot group statistics"
- Sijbers, J.; den Dekker, A. J.; Raman, E.; Van Dyck, D. (1999). "Parameter estimation from magnitude MR images". International Journal of Imaging Systems and Technology. 10 (2): 109–114. CiteSeerX 10.1.1.18.1228. doi:10.1002/(sici)1098-1098(1999)10:2<109::aid-ima2>3.0.co;2-r.
- den Dekker, A. J.; Sijbers, J. (2014). "Data distributions in magnetic resonance images: a review". Physica Medica. 30 (7): 725–741. doi:10.1016/j.ejmp.2014.05.002. PMID 25059432.
- Ahmadi, Hamed (2017-11-21). "A mathematical function for the description of nutrient-response curve". PLOS ONE. 12 (11): e0187292. Bibcode:2017PLoSO..1287292A. doi:10.1371/journal.pone.0187292. ISSN 1932-6203. PMC 5697816. PMID 29161271.
- "Rayleigh Probability Distribution Applied to Random Wave Heights" (PDF). United States Naval Academy.
{{cite web}}: CS1 maint: url-status (link)