Proceso adiabático

Un proceso sin transferencia de calor hacia o desde un sistema, de modo que Q = 0, se llama adiabático, y dicho sistema se dice que está adiabáticamente aislado.[1][2] La suposición simplificadora que se hace con frecuencia es que un proceso es adiabático. Por ejemplo, se supone que la compresión de un gas dentro de un cilindro de un motor ocurre tan rápidamente que, en la escala de tiempo del proceso de compresión, una pequeña parte de la energía del sistema puede transferirse en forma de calor a los alrededores. Aunque los cilindros no están aislados y son bastante conductores, ese proceso se idealiza para que sea adiabático. Lo mismo puede decirse del proceso de expansión de dicho sistema.

La suposición de aislamiento adiabático es útil y, a menudo, se combina con otras idealizaciones similares para calcular una buena primera aproximación del comportamiento de un sistema. Por ejemplo, según Laplace, cuando el sonido viaja en un gas, no hay tiempo para la conducción de calor en el medio, por lo que la propagación del sonido es adiabática. Para tal proceso adiabático, el módulo de elasticidad (Módulo de Young) se puede expresar como E = γP, donde γ es la relación de calores específicos a presión constante y a volumen constante (γ = C_p/C_v) y P es la presión del gas.

La compresión adiabática de un gas provoca un aumento de la temperatura del gas. La expansión adiabática contra la presión, o un resorte, provoca un descenso de la temperatura. En cambio, la expansión libre es un proceso isotérmico para un gas ideal.

El calentamiento adiabático se produce cuando la presión de un gas aumenta por el trabajo realizado sobre él por su entorno, por ejemplo, un pistón comprimiendo un gas contenido dentro de un cilindro y aumentando la temperatura donde en muchas situaciones prácticas la conducción de calor a través de las paredes puede ser lenta comparada con el tiempo de compresión. Esto encuentra aplicación práctica en motores diésel que dependen de la falta de disipación de calor durante la carrera de compresión para elevar la temperatura del vapor de combustible lo suficiente como para encenderlo.

El calentamiento adiabático se produce en la atmósfera terrestre cuando una masa de aire desciende, por ejemplo, en un viento catabático, viento foehn o viento Chinook que fluye cuesta abajo sobre una cordillera. Cuando un paquete de aire desciende, aumenta su presión. Debido a este aumento de presión, el volumen de la parcela disminuye y su temperatura aumenta, ya que se realiza trabajo sobre la parcela de aire, aumentando así su energía interna, que se manifiesta por un aumento de la temperatura de esa masa de aire. El paquete de aire sólo puede disipar lentamente la energía por conducción o radiación (calor), y en una primera aproximación puede considerarse aislado adiabáticamente y el proceso un proceso adiabático.

El enfriamiento adiabático se produce cuando la presión sobre un sistema aislado adiabáticamente disminuye, lo que le permite expandirse y, por tanto, realizar un trabajo sobre su entorno. Cuando se reduce la presión aplicada sobre un paquete de gas, se permite que el gas del paquete se expanda; a medida que aumenta el volumen, la temperatura desciende al disminuir su energía interna. El enfriamiento adiabático se produce en la atmósfera terrestre con la elevación orográfica y las ondas de sotavento, y esto puede formar pileus o nubes lenticulares.

Debido en parte al enfriamiento adiabático en zonas montañosas, en algunas partes del desierto del Sáhara se producen nevadas con poca frecuencia.[4]

El enfriamiento adiabático no tiene por qué implicar un fluido. Una técnica utilizada para alcanzar temperaturas muy bajas (milésimas e incluso millonésimas de grado por encima del cero absoluto) es a través de la desmagnetización adiabática, donde el cambio de campo magnético en un material magnético se utiliza para proporcionar enfriamiento adiabático. Además, el contenido de un universo en expansión puede describirse (en primer orden) como un fluido que se enfría adiabáticamente. (Véase Muerte térmica del universo).

El magma ascendente también experimenta un enfriamiento adiabático antes de la erupción, particularmente significativo en el caso de magmas que ascienden rápidamente desde grandes profundidades como las kimberlitas.[5]

En el manto convectivo de la Tierra (la astenosfera) bajo la litosfera, la temperatura del manto es aproximadamente adiabática. El ligero descenso de la temperatura con la profundidad se debe a la disminución de la presión cuanto más superficial es el material en la Tierra.[6].

Tales cambios de temperatura pueden cuantificarse utilizando la ley de los gases ideales, o la ecuación hidrostática para procesos atmosféricos.

En la práctica, ningún proceso es realmente adiabático. Muchos procesos se basan en una gran diferencia en las escalas de tiempo del proceso de interés y la tasa de disipación de calor a través de un límite del sistema, y por lo tanto se aproximan mediante el uso de una suposición adiabática. Siempre hay alguna pérdida de calor, ya que no existen aislantes perfectos.

Joule, en su célebre experimento sobre expansión libre, demostró que la energía interna de un gas perfecto era independiente del volumen (V), o la presión (P), solo función de la temperatura.

Esta conclusión conduce a que, para un gas ideal:

${\displaystyle {\text{(a)}}\qquad dU=n\ C_{v}\ dT=\delta Q-\delta W}$

Pero en la expansión adiabática:

${\displaystyle {\text{(b)}}\qquad \delta Q=0;\qquad \delta W=P\ \delta V}$

Con lo que se obtiene la siguiente relación:

${\displaystyle {\text{(c)}}\qquad \delta U=n\ C_{v}\ \delta T=-P\ \delta V}$

En el gas ideal se cumple:

${\displaystyle P\ V=n\ R\ T}$

${\displaystyle C_{p}-C_{v}=R}$

${\displaystyle \gamma =C_{p}/C_{v}}$

Los valores ${\displaystyle C_{p}}$ y ${\displaystyle C_{v}}$ son función del número de átomos en la molécula.

Despejando ${\displaystyle P}$ y sustituyendo ${\displaystyle P}$ y ${\displaystyle R}$ en la Ec.(c) queda, la relación diferencial:

${\displaystyle {\text{(d)}}\qquad {\frac {dT}{T}}=-{\frac {\left(\gamma -1\right)\ dV}{V}}}$

E integrando entre los estados inicial y final:

${\displaystyle {\text{(e)}}\qquad {\frac {T_{f}}{T_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma -1\right)}}$

Teniendo en cuenta que al trabajar con gases perfectos se cumple ${\displaystyle T=PV/nR}$, la Ec.(e) puede ponerse:

${\displaystyle \qquad {\frac {P_{f}\ V_{f}}{P_{i}\ V_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma -1\right)}\qquad \to \qquad {\frac {P_{f}}{P_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma \right)}}$

Finalmente:

${\displaystyle {\text{(f)}}\qquad P_{f}V_{f}^{\gamma }=P_{i}V_{i}^{\gamma }=Constante}$

operando sobre Ec.(e) y Ec.(f):

${\displaystyle {\text{(g)}}\qquad {\frac {T_{f}}{T_{i}}}=\left({\frac {P_{f}}{P_{i}}}\right)^{\left({\frac {\gamma -1}{\gamma }}\right)}}$

Asumiremos que el sistema es un gas monoatómico, por lo que :${\displaystyle C_{V}={3 \over 2}R}$ donde R es la constante universal de los gases.

Dado ${\displaystyle \Delta P}$ y ${\displaystyle \Delta V}$ entonces ${\displaystyle W=P\Delta V}$ y ${\displaystyle \Delta U={3 \over 2}nR\Delta T={3 \over 2}\Delta (PV)={3 \over 2}(P\Delta V+V\Delta P)\qquad (3)}$

Ahora sustituyendo las ecuaciones (2) y (3) en la ecuación (1) obtenemos

${\displaystyle -P\Delta V={3 \over 2}P\Delta V+{3 \over 2}V\Delta P}$

simplificando

${\displaystyle -{5 \over 2}P\Delta V={3 \over 2}V\Delta P}$

dividiendo ambos lados de la igualdad entre PV

${\displaystyle -5{\Delta V \over V}=3{\Delta P \over P}}$

Aplicando las normas del cálculo diferencial (es decir integrando a ambos lados) obtenemos que

${\displaystyle -5\Delta (\operatorname {ln} V)=3\Delta (\operatorname {ln} P)}$

que tomando :${\displaystyle \Delta lnV=(lnV-lnV_{0});\Delta lnP=(lnP-lnP_{0})}$ se puede expresar como

${\displaystyle {\operatorname {ln} P-\operatorname {ln} P_{0} \over \operatorname {ln} V-\operatorname {ln} V_{0}}=-{5 \over 3}}$

Para ciertas constantes ${\displaystyle P_{0}}$ y ${\displaystyle V_{0}}$ del estado inicial. Entonces

${\displaystyle {\operatorname {ln} (P/P_{0}) \over \operatorname {ln} (V/V_{0})}=-{5 \over 3},}$

${\displaystyle \operatorname {ln} \left({P \over P_{0}}\right)=-5/3\operatorname {ln} \left({V \over V_{0}}\right)}$

elevando al exponente ambos lados de la igualdad

${\displaystyle \left({P \over P_{0}}\right)=\left({V \over V_{0}}\right)^{-5/3}}$

eliminando el signo menos

${\displaystyle \left({P \over P_{0}}\right)=\left({V_{0} \over V}\right)^{5/3}}$

por lo tanto

${\displaystyle \left({P \over P_{0}}\right)\left({V \over V_{0}}\right)^{5/3}=1}$

y

${\displaystyle PV^{5/3}=P_{0}V_{0}^{5/3}=P_{0}V_{0}^{\gamma }=\operatorname {constante} .}$

Durante un proceso adiabático, la energía interna del fluido que realiza el trabajo debe necesariamente decrecer.

Esquema de una expansión adiabática.

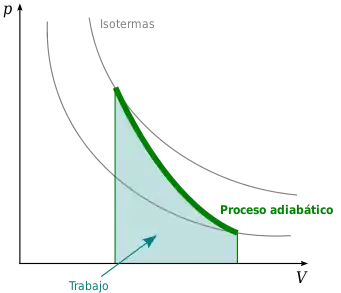
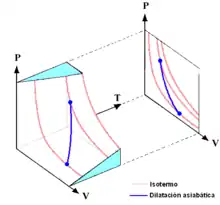
Las propiedades de las curvas adiabáticas en un diagrama P-V son las siguientes:

1. Cada adiabática se aproxima asintóticamente a ambos ejes del diagrama P-V (al igual que las isotermas).
2. Cada adiabática se interseca con cada isoterma en un solo punto.
3. Una curva adiabática se parece a una isoterma, excepto que durante una expansión, una adiabática pierde más presión que una isoterma, por lo que inclinación es mayor (es más vertical).
4. Si las isotermas son cóncavas hacia la dirección "noreste" (45°), entonces las adiabáticas son cóncavas hacia la dirección "este noreste" (31°).
5. Si adiabáticas e isotermas se dibujan separadamente con cambios regulares en la entropía y temperatura, entonces a medida que nos alejamos de los ejes (en dirección noreste), parece que la densidad de las isotermas permanece constante, pero la densidad de las adiabáticas disminuye. La excepción se encuentra muy cerca del cero absoluto, donde la densidad de las adiabáticas cae fuertemente y se hacen muy raras (Véase también: Teorema de Nernst).

Según se dedujo anteriormente, la ecuación que describe un proceso adiabático del gas ideal, en un proceso reversible: ${\displaystyle PV^{\gamma }=\operatorname {constante} }$ donde P es la presión del gas, V su volumen y ${\displaystyle \gamma ={C_{P} \over C_{V}}}$ el coeficiente adiabático, siendo ${\displaystyle C_{P}}$ el calor específico molar a presión constante y ${\displaystyle C_{V}}$ el calor específico molar a volumen constante.

Para un gas monoatómico ideal, ${\displaystyle \gamma =5/3}$. Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire) ${\displaystyle \gamma =7/5=1,4}$

Al no haber suministro externo de calor, cualquier trabajo (W) realizado será a expensas de la energía U, En la fórmula:

${\displaystyle PV^{\gamma }=\operatorname {K} }$

hacemos un pequeño cambio, entonces quedaría así:

${\displaystyle P=K/V^{\gamma }\qquad \qquad \qquad (4)}$

Ahora derivando la fórmula del trabajo e integrándola a la vez tenemos:

${\displaystyle \int _{1}^{2}\,dW}$ =${\displaystyle \int _{1}^{2}\,PdV\qquad \qquad \qquad (5)}$

Ahora reemplazamos la (4) en la (5):

${\displaystyle \int _{1}^{2}\,K/{V^{\gamma }}dV}$

Ahora sabemos que "K" es una constante, por lo cual, esta sale de la integral:

${\displaystyle K\int _{1}^{2}\,1/{V^{\gamma }}dV}$

luego vemos que nos queda todo en función del volumen entonces lo integramos:

${\displaystyle (KV^{1-{\gamma }})/(1-{\gamma })}$

como sabemos que:

${\displaystyle PV^{\gamma }=\operatorname {K} }$

entonces reemplazamos en la ecuación:

${\displaystyle PV^{\gamma }(V^{1-{\gamma }})_{1}^{2}/(1-{\gamma })}$

y multiplicamos:

${\displaystyle (P_{2}V_{2}^{\gamma }V_{2}^{1-{\gamma }}-P_{1}V_{1}^{\gamma }V_{1}^{1-{\gamma }})/(1-{\gamma })}$

luego de resolver la ecuación nos quedará esta forma:

${\displaystyle [P_{2}V_{2}-P_{1}V_{1}]/(1-{\gamma })}$

y por definición nos quedaría:

${\displaystyle \Delta (PV)/(1-{\gamma })}$

que al final nos dará:

${\displaystyle nR\Delta T/(1-{\gamma })}$

y esto será igual al trabajo:

${\displaystyle \ W=(P_{2}V_{2}-P_{1}V_{1})/(1-{\gamma })=nR(T_{2}-T_{1})/(1-{\gamma })}$

Existen tres relaciones en el enfriamiento adiabático del aire:

1. La relación ambiente de la atmósfera, que es la proporción a la que el aire se enfría a medida que se gana altitud.
2. La tasa seca adiabática, es de unos -1° por cada 100 metros de subida.
3. La tasa húmeda adiabática, es de unos -0,6° - 0,3º por cada 100 metros de subida.

La primera relación se usa para describir la temperatura del aire circundante a través del cual está pasando el aire ascendente. La segunda y tercera proporción son las referencias para una masa de aire que está ascendiendo en la atmósfera. La tasa seca adiabática se aplica a aire que está por debajo del punto de rocío, por ejemplo, si no está saturado de vapor de agua, mientras que la tasa húmeda adiabática se aplica a aire que ha alcanzado su punto de rocío. El enfriamiento adiabático es una causa común de la formación de nubes.

El enfriamiento adiabático no tiene por qué involucrar a un fluido. Una técnica usada para alcanzar muy bajas temperaturas (milésimas o millonésimas de grado sobre el cero absoluto) es la desimanación adiabática, donde el cambio en un campo magnético en un material magnético es usado para conseguir un enfriamiento adiabático.

En mecánica cuántica una transformación adiabática es un cambio lento en el Hamiltoniano cuántico ${\displaystyle {\hat {H}}\,}$ que describe el sistema y que resulta en un cambio de los valores propios del Hamiltoniano pero no de sus estados propios, lo que se conoce como cruce evitado. Por ejemplo, si un sistema comienza en su estado fundamental permanecerá en el estado fundamental a pesar de que las propiedades de este estado pueden cambiar. Si en tal proceso se produce un cambio cualitativo en las propiedades del estado fundamental, como por ejemplo un cambio de spin la transformación se denomina transición de fase cuántica. Las transiciones de este tipo son transiciones de fase prohibidas por la mecánica clásica.

• Wikcionario tiene definiciones y otra información sobre adiabático.
• Motor adiabático
• Pistón de fuego
• Criterio de signos termodinámico
• Proceso termodinámico
• Sistema termodinámico