Compuesto de cubo y octaedro
El compuesto de cubo y octaedro puede verse como la estelación de un poliedro o como un poliedro compuesto.[1]
| Compuesto de cubo y octaedro | |
|---|---|
 | |
| Tipo | Compuesto |
| Diagrama de Coxeter-Dynkin | |
| Núcleo de la estelación | Cuboctaedro |
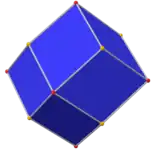
| Envolvente convexa | Rombododecaedro |
| Índice | W43 |
| Poliedros | 1 octaedro 1 cubo |
| Caras | 8 triángulos 6 cuadrados |
| Aristas | 24 |
| Vértices | 14 |
| Grupo de simetría | Octaédrico (Oh) |
Construcción
Las 14 coordenadas cartesianas de los vértices del compuesto son:
- 6: (±2, 0, 0), ( 0, ±2, 0), ( 0, 0, ±2)
- 8: (±1, ±1, ±1)
Como un compuesto
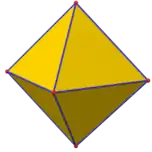
Puede verse como el compuesto de un octaedro y de un cubo. Es uno de los cuatro compuestos construidos a partir de un sólido platónico o de un sólido de Kepler-Poinsot y su dual.
Tiene simetría octaédrica (Oh) y comparte los mismos vértices que un rombododecaedro.
Esto puede verse como el equivalente tridimensional del "octagrama", el compuesto de dos cuadrados ({8/2}); esta serie continúa hasta el infinito, siendo el equivalente en cuatro dimensiones el compuesto de teseracto y 16-celdas.
Un cubo y su octaedro dual |
El hexágono del medio es el polígono de Petrie de ambos sólidos.
Como una estelación
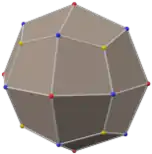
También es la primera estelación del cuboctaedro, y como tal figura en el índice de modelos de Wenninger con el número 43.
Se puede ver como un cuboctaedro con pirámides agregadas a cada cara triangular.
Las caras de la estelación para construir la figura son:
Véase también
- Compuesto de dos tetraedros
- Compuesto de dodecaedro e icosaedro
- Compuesto de pequeño dodecaedro estrellado y gran dodecaedro
- Compuesto de gran dodecaedro estrellado y gran icosaedro
Referencias
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 978-0-521-09859-5.