Cubo (aritmética)
En aritmética y álgebra, el cubo de un número n es la tercera potencia —el resultado de multiplicar por sí mismo tres veces:[1]

En geometría, es la ecuación para obtener el volumen de un cubo (hexaedro regular) de arista a:
Propiedades
A diferencia del cuadrado de un número, no existe el número cubo más pequeño, debido a que se incluyen los números negativos. Por ejemplo, (−4) × (−4) × (−4) = −64. Para cualquier n, (−n)3 = −(n3). Sin embargo, es posible en el caso de los números naturales; el cubo de 1 es la tercera potencia más pequeña en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): N .
A diferencia de los cuadrados perfectos, los cubos perfectos no tienen una pequeña cantidad de posibilidades excepto para los dos últimos dígitos, excepto para los cubos divisibles por 5, donde únicamente 25 y 75 pueden ser los dos últimos dígitos; cualquier par de dígitos con los últimos dígitos impares puede ser un cubo perfecto. Con los cubos pares, hay una considerable restricción, solo para 00, i2, p4, i6 y p8 puede que los dos últimos dígitos de un cubo perfecto (donde i significa cualquier dígito impar y p para dígitos pares). Algunos números cúbicos son también números cuadrados, por ejemplo 64 es un cuadrado (8 × 8) y al mismo tiempo un cubo (4 × 4 × 4); esto ocurre si y solo si es una sexta potencia perfecta. Cabe esa posibilidad si el expontente k es múltiplo de 6, para la duodécima, décima octava potencia, etc.

Sin embargo, es fácil ver que la mayoría de los números no son cubos perfectos a causa de que todos los cubos perfectos deben tener una raíz digital 1, 8 o 9. De esta forma, la raíz digital de cualquier número queda determinada por el resto del número cuando es dividido entre 3:
- Si el número es divisible entre 3, su cubo tiene como raíz digital al 9;
- Si tiene como resto 1 cuando es dividido entre 3, su cubo tiene la raíz digital igual a 1;
- Si tiene como resto 2 cuando es dividido entre 3, su cubo tiene como raíz digital 8.
Cada entero positivo puede ser escrito como la suma de nueve cubos o incluso menos, véase problema de Waring. Este límite superior de nueve cubos no puede ser reducido ya que, por ejemplo, 23 no puede ser escrito como la suma de menos de nueve cubos:
- 23 = 23 + 23 + 13 + 13 + 13 + 13 + 13 + 13 + 13
El número m es un cubo perfecto si y solo si pueden ordenarse m puntos en un cubo, por ejemplo 3 × 3 × 3 = 27. La suma de los primeros n cubos perfectos es un n-ésimo número triangular al cuadrado:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle 1^3+2^3+...+n^3 = \left ( \frac{n(n+1)}{2} \right )^2}
Por ejemplo, la suma de los primeros cinco números cubos perfectos, 13 + 23 + 33 + 43 + 53, es igual a la suma de los cinco primeros números triangulares 152 que es 225.
Otras características
- (mn)3 = m3n3
- Si m es múltiplo de n: (m÷n) = m3 ÷ n3
- (m ± n)3 = m3 ± 3m2n +3mn2 ± n3
- Si m > n, entonces m3 > n3 (función creciente)
- Sea H = {n3/ n es n. natural}, H tiene mínimo
- Si n > 1, entonces n3 > n2 > n
- m3+n3 = (m2-mn+n2)(m+n)
- Hay una identidad análoga para la diferencia de cubos, basta en la anterior, cambiar n por -n
- Si al producto de tres términos consecutivos de una progresión aritmética, de término inicial m y diferencia r, se le agrega kr2, donde k es el término intermedio, se obtiene un cubo perfecto para k, m y r enteros positivos.
- El producto de tres términos consecutivos de una progresión geométrica es un cubo perfecto.
- La media geométrica de tres números siempre existe sin importar el signo de los números.[2]
- Si al producto de tres números naturales consecutivos se le agrega el término intermedio, se obtiene el cubo del intermedio. Así 11×12×13 + 12 = 1 728 = 123
- x3+y3+z3 ≥ 3xyz,[3] donde x, y, z son números reales positivos; la igualdad se verifica cuando los 3 números son iguales.
Relación con otras funciones
La función inversa a encontrar un número cuyo cubo es n se denomina extracción de la raíz cúbica de n. La operación es similar a encontrar la arista de un cubo de volumen conocido. También se dice que n elevado un tercio.
Suma interesante
- .
En vez de hacer tres depósitos cúbicos de aristas 17, 14 y 7 m respectivamente, si se reemplaza por un depósito cúbico de arista 20 m, se ahorra en costo de material y se usa en menos cantidad. Pero la misma capacidad.
Casos vinculados
- Un clásico problema de cubos, demoró en hallar su solución, por la irracionalidad de un factor numérico. Se trataba de calcular la arista de un cubo que tenga el doble de volumen del cubo del oráculo de Delfos.[5] (Véase duplicación del cubo)
- Un dato al cubo aparece en la fórmula del volumen de un cubo, de una esfera, tetraedro regular, de un octaedro, dodecaedro, icosaedro regulares, en la suma de los cuadrados de los primeros n naturales, que conlleva tres sumandos o términos:[6]
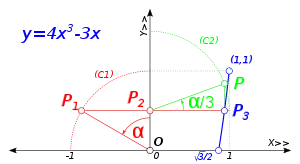
- Así mismo, se puede utilizar una curva cúbica para determinar la trisección de un ángulo arbitrario, partiendo de la fórmula trigonométrica del coseno del ángulo triple: (véase Identidades y fórmulas de trigonometría)
- En efecto, haciendo que y que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle x=\cos \theta} , se obtiene la parábola de tercer grado[7]
- cuya representación en el intervalo (es decir, ) permite determinar gráficamente el coseno del ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \alpha/3} a partir del coseno del ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \alpha , tal como se puede observar en la imagen adjunta. La solución gráfica permite obtener directamente la trisección de ángulos comprendidos entre 0° y 90°. Para ángulos mayores de 90°, basta con realizar la trisección tras restar 90° al ángulo dado, y sumar a continuación 30° al resultado obtenido.
Referencias
- Definición de cubo: DRAE.
- Adaptado de "Álgebra" de Rees- Sparks ISBN 978-968-6708-073
- Aplicando la relación entre la media aritmética y geométrica
- Formulario de ciencia"El cerebrito" de UCH, Lima 2013
- Bell: Historia de las matemáticas
- Bronshtein et al: Manual de Matemáticas
- Weisstein, Eric W. «Cubo (aritmética)». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Enlaces externos
- Suma de cuatro cubos Aplicación web que descompone un número entero en otro no congruente 4 o 5 (mod 9) en suma de cuatro cubos.