Deltoide recto
En la geometría euclídea, un deltoide recto es un tipo de deltoide (un cuadrilátero cuyos cuatro lados se pueden agrupar en dos pares de lados de igual longitud que son adyacentes entre sí) que se puede inscribir en un círculo.[1] Es decir, es un deltoide que posee un circuncírculo (es decir, es cíclico). Por lo tanto, es un cuadrilátero convexo y tiene dos ángulos rectos opuestos.[2] Si hay exactamente dos ángulos rectos, cada uno debe estar entre dos lados de diferentes longitudes. Todos los deltoides rectos son cuadriláteros bicéntricos (cuadriláteros con un circuncírculo y un incírculo), ya que todos los deltoides poseen un incírculo. Una de las diagonales (la que es una línea de simetría) divide el polígono en dos triángulos rectángulos, y también es un diámetro del circuncírculo.
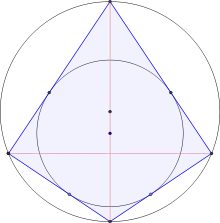
En un cuadrilátero tangencial (uno que posee un incírculo), los cuatro segmentos de línea entre el centro del círculo y los puntos donde es tangente al cuadrilátero, dividen el cuadrilátero en cuatro deltoides rectos.
Caso especial
Un caso especial de deltoide recto es el cuadrado, cuando las diagonales tienen la misma longitud, y el incírculo y el circuncírculo son concéntricos.
Caracterización
Un deltoide se dice que es recto si y solo si posee un circuncírculo (por definición). Esto es equivalente a ser un deltoide con dos ángulos rectos opuestos.
Fórmulas métricas
Dado que un deltoide recto se puede dividir en dos triángulos rectángulos, las siguientes fórmulas métricas se deducen fácilmente de las propiedades bien conocidas de los triángulos rectángulos. En un deltoide recto ABCD donde los ángulos opuestos B y D son ángulos rectos, los otros dos ángulos se pueden calcular a partir de
donde a = AB = AD y b = BC = CD . El área de un deltoide recto es
La diagonal CA, que es un eje de simetría, tiene la longitud
y, dado que las diagonales son perpendiculares (un deltoide recto es un cuadrilátero ortodiagonal con área ), la otra diagonal BD tiene la longitud
El radio de la circunferencia circunscrita es (según el teorema de Pitágoras)
y, dado que todos los deltoides son cuadriláteros tangenciales, el radio del círculo viene dado por
donde s es el semiperímetro.
El área se da en términos del circunradio R y del inradio r como [3]
Si se toman los segmentos que se extienden desde la intersección de las diagonales hasta los vértices en el sentido de las agujas del reloj , ,, y , entonces,
Este es un resultado directo del teorema de la media geométrica.
Dualidad
El polígono dual de un deltoide recto es un trapezoide tangencial isósceles.[1]
Definición alternativa
A veces, un deltoide recto se define como un deltoide con al menos un ángulo recto.[4] Si solo hay un ángulo recto, debe estar entre dos lados de igual longitud; en este caso, las fórmulas dadas arriba no se aplican.
Referencias
- Michael de Villiers, Some Adventures in Euclidean Geometry,
- De Villiers, Michael (1994), «The role and function of a hierarchical classification of quadrilaterals», For the Learning of Mathematics 14 (1): 11-18.
- Josefsson, Martin (2012), «Maximal Area of a Bicentric Quadrilateral», Forum Geometricorum 12: 237-241..
- 1728 Software Systems, Kite Calculator, accessed 8 October 2012