Factorización
En matemáticas la factorización es una técnica que consiste en la descomposición en factores de una expresión algebraica (que puede ser un número, una suma o resta, una matriz, un polinomio, etc.) en forma de producto. Existen distintos métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que reciben el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles.
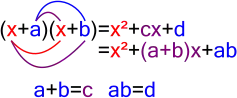
Lo contrario de la factorización de polinomios es la expansión, la multiplicación de los factores juntos polinómicas a un polinomio "ampliado", escrito como una simple suma de términos.
El teorema fundamental de la aritmética cubre la factorización de números enteros, y para la factorización de polinomios, el teorema fundamental del álgebra. La factorización de números enteros muy grandes en producto de factores primos requiere de algoritmos sofisticados, el nivel de complejidad de tales algoritmos está a la base de la fiabilidad de algunos sistemas de criptografía asimétrica como el RSA.
Enteros
Por el teorema fundamental de la aritmética, cada entero positivo tiene una única descomposición en números primos (factores primos), es decir, se puede representar de forma única como producto de factores primos.
Polinomios
Las técnicas modernas para la factorización de polinomios son rápidas y eficientes, pero el uso de las ideas matemáticas sofisticadas (véase Factorización de polinomios). El uso de ecuaciones cuadráticas para modelar situaciones y resolverlas usando la factorización. La factorización es una técnica que consiste en la descomposición de una expresión matemática, en forma de producto.
Mientras que la noción general de factorización solo significa escribir una expresión como un producto de las expresiones más simples, el término vago "simple" se definirá con mayor precisión para las clases especiales de expresiones. Cuando existe factorización de polinomios, esto significa que los factores son para ser polinomios de grado más pequeño. Así, mientras es una factorización de la expresión, no es una factorización polinómica ya que los factores no son polinomios.[1] Además, la factorización de un término constante, como en no se consideraría una factorización polinómica dado que uno de los factores no tiene un grado menor que la expresión original.[2] Otra cuestión se refiere a los coeficientes de los factores. En tratamientos básicos es deseable tener los coeficientes de los factores del mismo tipo que los coeficientes del polinomio original, es decir factorización de polinomios con coeficientes enteros en factores con coeficientes enteros, o factorización de polinomios con coeficientes reales en polinomios con coeficientes reales . No siempre es posible hacer esto, y un polinomio que no puede ser factorizado de esta forma se dice que es irreducible sobre este tipo de coeficiente. Por lo tanto, x² -2 es irreducible sobre los números enteros y x² + 4 es irreducible sobre los números reales. En el primer ejemplo, los números enteros 1 y -2 pueden también ser considerados como números reales, y si es así, entonces muestra que este polinomio factores sobre los reales (a veces se dice que las divisiones de polinomios sobre los reales). Del mismo modo, ya que los números enteros 1 y 4 pueden ser pensados como números complejos y, por ende, x² + 4 tiene divisiones sobre los números complejos, es decir, .
El teorema fundamental del álgebra se puede establecer como: Todo polinomio de grado n con coeficientes de número complejo se divide por completo en factores lineales n. Los términos en estos factores, que son las raíces del polinomio, pueden ser reales o complejos. Desde raíces complejas de polinomios con coeficientes reales vienen en pares complejos conjugados, este resultado implica que cada polinomio con coeficientes reales se divide en lineales y / o factores cuadráticos irreducibles con coeficientes reales (porque cuando dos factores lineales con términos conjugados complejos se multiplican entre sí, el resultado es una cuadrática con coeficientes reales). A pesar de que la estructura de la factorización es conocida en estos casos, la búsqueda de los factores reales puede ser computacionalmente difícil, y por el teorema de Ruffini de los coeficientes y los términos aditivos en los factores pueden no ser expresable en términos de radicales.
Un polinomio de grado n se puede factorizar en un producto de polinomios de grado con y . Concretamente se refiere a factorizar un polinomio con coeficientes en un cuerpo dado o en los números enteros en polinomios irreducibles con coeficientes en el mismo dominio.
Por ejemplo el polinomio P(x) de grado 5 se puede factorizar como producto de un polinomio de grado 3 y un polinomio de grado 2:
Usos
La factorización de polinomios se emplea en:
- La resolución de una ecuación algebraica P(x); usualmente se considera el factor x-a y se tantea mediante la división sintética de Ruffini. Si el resto es cero, cabe la igualdad P(x)= H(x)(x-a). Y se reitera el procedimiento.
- La adición de fracciones algebraicas.[3]
- Integración de funciones racionales, para lo cual se descompone en fracciones parciales.[4]
Historia de la factorización
Los estudiantes que se introducen en la factorización como principal método de resolución de ecuaciones cuadráticas que se sorprenda al saber que es uno de los más nuevos métodos para resolverlos. Vera Sanford señala en su A Short History of Mathematics (1930)[5] que "en vista de la actual énfasis dado a la solución de ecuaciones cuadráticas por factorización, es interesante observar que este método no se utilizó hasta el trabajo de Harriot en 1631. Incluso en este caso, sin embargo, el autor hace caso omiso de los factores que dan lugar a las raíces negativas. "Harriot murió en 1621, y al igual que todos sus libros, este, Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, fue publicado después de su muerte. Un artículo sobre Harriot en el sitio web de la historia matemática de la Universidad de San Andrews dice que en su escritura personal en la resolución de ecuaciones Harriot hizo uso de soluciones tanto positivos como negativos, pero su editor, Walter Warner, no presentó en su libro. método de factorización de Harriot puede ser distinta de lo que los estudiantes esperan modernas. En la primera sección (Sección Prima) Harriot dibuja tablas para ilustrar la suma, resta, multiplicación y división de monomios, binomios, y trinomio. Luego, en la segunda sección que muestra una multiplicación más directa que proporciona la base para su método de factorización. Él establece la ecuación de aa − ba + ca = + bc, y muestra que esta coincida con la forma de multiplicación que ha proporcionado previamente como,
a − b aa − ba (===) (Harriot usa el signo igual de largo introducido por Robert Recorde) a + c ca − bc
Así factorizando los cuatro términos de la expresión ajustada aa − ba + ca − bc. Este ejemplo puede ser visto en la página 16 de the Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas.
Harriot escribe un formulario para cada una de las posibilidades de (a ± b)(a ± c) con a siendo lo desconocido (donde podríamos utilizar x hoy) y luego, cuando se deben incorporar recoge en una de las formas que responden. Al separar el coeficiente lineal en dos partes que es capaz de romper el problema en una de las formas.
Métodos generales
Hay sólo unos pocos métodos generales que pueden ser aplicados a cualquier polinomio ya sea en una variable (la univariate case) o varias variables (el caso de multivariables).
Factor común
Encontrando, por inspección, el monomio que es el máximo común divisor de todos los términos del polinomio y factorizándolo como un factor común que es una aplicación de la ley distributiva. Este es comúnmente el más usado en la técnica de factorización. Por ejemplo:[6]
Factor común por agrupación de términos
Un método que a veces es útil, pero no garantiza que funcione, es la factorización mediante la agrupación.
La factorización por agrupación se realiza mediante la colocación de los términos en el polinomio en dos o más grupos, donde cada grupo se puede factorizar mediante un método conocido. Los resultados de estas factorizaciones parciales se pueden combinar a veces para dar una factorización de la expresión original.
Por ejemplo, para factorizar el polinomio
- :
- Agrupar los términos similares,
- Factorizar por el máximo común divisor en cada agrupación,
- Nuevamente factorizar el factor común del binomio,
Mientras que la agrupación no puede conducir a una factorización en general, si la expresión polinómica no ha influido, consta de cuatro términos y es el resultado de multiplicar dos binomios( por la ley distributiva), entonces la técnica de agrupación puede conducir a una factorización, como en el ejemplo anterior.
Teorema del factor
Para un polinomio de una variable, p(x), el teorema del factor establece que a es una raíz del polinomio (que es, p(a) = 0, también llamado un cero del polinomio) si y solo si (x - a) es un factor de p(x). El otro factor en una factorización de p(x) puede ser obtenido por la división polinómica o división sintética.
Por ejemplo, consideremos el polinomio Por inspección vemos que 1 es la raíz de este polinomio (observemos que los coeficientes se suman a 0), entonces (x - 1)es un factor del polinomio. Por división de larga tenemos
Caso de una variable, usando propiedades de las raíces
Cuando el polinomio de una variable es completamente factorizado en factores lineales (factores de un grado), todas las raíces del polinomio son visibles y multiplicando los factores juntos de nuevo, se puede observar la relación entre las raíces y los coeficientes. Formalmente, estas relaciones se conocen como fórmulas de Viète. Estas fórmulas no ayudan a factorizar el polinomio excepto como una guía para hacer buenas conjeturas que sean en las posibles raíces. Sin embargo, si se conoce alguna información adicional acerca de las raíces, esto se puede combinar con las fórmulas para obtener las raíces y por lo tanto la factorización.
Por ejemplo,[7] podemos factorizar si sabemos que la suma de dos de sus raíces es cero. Deja que y sean las tres ráices de este polinomio. A continuación, las fórmulas de Viète son:
Asumiendo que inmediatamente da y reduce las otras dos ecuaciones a De este modo las raíces son 5, 4 y -4 y tenemos
Hallando raíces racionales
Si un (una variable) polinomio, f(x), tiene una raíz racional, p/q (p y q son enteros y q ≠ 0), entonces por el teorema del factor f(x) tiene el factor,
Si, además, el polinomio f(x) tiene coeficientes enteros, entonces q debe dividir uniformemente la parte entera del máximo común divisor de los términos del polinomio., y, en la factorización de f(x), sólo el factor (qx - p) será visible.
Si un (una variable) polinomio con coeficientes enteros, dice,
tiene una raíz racional p/q, donde p y q son enteros que son números primos entre sí, entonces por el teorema de la raíz racional p es un divisor entero de an y q es un divisor entero de a0.[8]
Si queríamos factorizar el polinomio podríamos buscar raíces racionales p/q donde p divide -6, q divide 2 y p u q no tienen factor común más grande que 1. Por inspección vemos que este polinomio no tiene raíces negativas. Asumir que q = 2 (de lo contrario estaríamos buscando las raíces de números enteros), sustituir x = p/2 y colocar la igualdad del polinomio a 0.
Multiplicando por 4, obtenemos que tendrá una solución entera de 1 o 3 si el polinomio original tenía una raíz racional del tipo que buscamos. Desde que 3 es una solución de esta ecuación (y no es 1), el polinomio original tenía la raíz racional 3/2 y el factor correspondiente (2x - 3). Por la división larga polinómica tenemos la factorización
Para un polinomio de segundo grado con coeficientes enteros, teniendo raíces racionales, las consideraciones anteriores llevan a una técnica de factorización conocido como el método ac de factorización.[9] Suponiendo que el polinomio de segundo grado con coeficientes enteros es:
y tiene raíces racionales, p/q y u/v. (Si el discriminante, , es un número cuadrado éstos existen, de lo contrario tenemos soluciones irracionales o complejos, y no habrá ningunas raíces racionales.) Ambos q y v deben ser divisores dea por lo que podemos escribir estas fracciones con un denominador común de a, que es, que se pueden escribir como -r/a y -s/a (el uso de los negativos es cosmético y conduce a un resultado final más bonito.) Entonces,
Así, tenemos:
Donde rs = ac y r + s = b. El método ac para factorizar el polinomio de segundo grado es encontrar r y s, los dos factores del número ac cuya suma es b y luego utilizarlos en la fórmula de la factorización de la ecuación cuadrática de origen encima.
Como ejemplo, consideremos el polinomio de segundo grado:
La inspección de los factores de ac = 36 conduce a 4 + 9 = 13 = b.
Patrones reconocibles
Mientras se está tomando el producto de dos (o más) las expresiones pueden hacerse siguiendo un algoritmo de multiplicación, el proceso inverso de la factorización se basa con frecuencia en el reconocimiento de un patrón en la expresión de tenerse en cuenta y recordando cómo surge un patrón. Los siguientes son algunos patrones bien conocidos.[10]
Diferencia de dos cuadrados
Un tipo común de factorización algebraica es para la diferencia de dos cuadrados. Es la aplicación de la fórmula
a cualquiera de los dos términos, si son o no son cuadrados perfectos.
Esta forma básica se utiliza a menudo con expresiones más complicadas que pueden no parecer a primera vista como la diferencia de dos cuadrados. Por ejemplo,
Suma o diferencia de cubos

Otra fórmula para la factorización es la suma o diferencia de dos cubos. La suma se puede factorizar por
y la diferencia por
Suma o diferencia de dos potencias n-ésimas
Las factorizaciones n-ésima de diferencias y sumas de potencias se pueden ampliar a cualquier potencia entera positiva n.
Para cualquier n, una factorización general es:
La fórmula correspondiente para la suma de dos potencias n-ésimas depende de si n es par o impar. Si n es impar, b puede se reemplazado por −b en la fórmula anterior, para dar
Si n es par, consideramos dos casos:
- Si n es una potencia de 2 entonces no se puede factorizar (más precisamente, irreducible sobre los números racionales).
- De otra manera, donde m es impar. En este caso tenemos,
En concreto, para algunos valores pequeños de n tenemos:
Suma o diferencia de dos potencias n-ésimas sobre el campo de los números algebraicos
Las factorizaciones anteriores dan factores con coeficientes en el mismo campo que las de la expresión de ser factorizada, por ejemplo, un polinomio con coeficientes racionales (± 1 en muchos casos anteriores) se divide en factores que por sí mismos tienen coeficientes racionales. Sin embargo, una factorización en factores con números algebraicos como coeficientes puede producir factores de menor grado, al igual que en las siguientes fórmulas que se pueden demostrar con ayuda de las raíces complejas conjugadas de
La suma de dos términos que tienen potencias pares iguales es factorizada
La diferencia de dos términos que tienen potencias pares iguales es factorizada
La suma o diferencia de dos términos que tienen potencias impares se factoriza
Por ejemplo, la suma o diferencia de dos potencias quintas se factoriza
y la suma de dos potencias cuartas se factoriza a
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle a^4 + b^4 = (a^2 - \sqrt 2 ab + b^2)(a^2 + \sqrt 2 ab + b^2).\! }
Expansiones binomiales
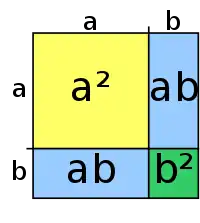
El teorema del binomio suministra patrones de coeficientes que permiten factorizaciones fácilmente reconocidos cuando el polinomio es una potencia de un binomio.
Por ejemplo, el trinomio cuadrado perfecto son los polinomios de segundo grado que se puede factorizar como se muestra a continuación:
y
Algunos polinomios cúbicos, se pueden factorizar como cubo perfecto de la siguiente manera:
y
En general, los coeficientes del polinomio expandido vienen dados por la 'enésima' fila del triángulo de Pascal. Los coeficientes de tienen el mismo valor absoluto, pero con signos alternados.
Otras fórmulas de factorización
El uso de fórmulas de raíces del polinomio
Cualquier polinomio de segundo grado de una variable (polinomios de la forma ) se puede factorizar sobre el campo de los números complejos utilizando la fórmula cuadrática, como sigue:
donde y son las dos raíces del polinomio, ya sean ambas reales o complejas en el caso donde a, b, c son todos reales, encontradas con la fórmula cuadrática.
La fórmula cuadrática es válida para todos los polinomios con coeficientes en cualquier campo (en particular, los números reales o complejos) excepto esos que tienen característica dos.[11]
También hay fórmulas para cúbicas y cuárticas, polinomios que se pueden utilizar de la misma manera. Sin embargo, no hay fórmulas algebraicas en términos de los coeficientes que se aplican a todos los polinomios de una variable de un grado más alto, por el teorema de Abel-Ruffini.
Suma de dos cuadrados
Si a y b representan números reales, entonces la suma de sus cuadrados puede ser escrita como el producto de números complejos. Esto produce la fórmula de factorización:
Por ejemplo, puede ser factorizada en .
Matrices
Una factorización de una matriz es la descomposición de esta en producto de matrices. Hay varios tipos de factorización de matrices; cada uno se usa en una clase particular de problemas.
Potencias
Para realizar la factorización de las bases de las potencias debemos hacer el factor común, es decir an tenemos que descomponerlo en factores primos. Por ejemplo, queremos factorizar 24 y ponerlo en forma de potencia haremos lo siguiente:
|
|
Entonces ya sabemos que 24 en forma de potencia es 23 · 3.[12]
Véase también
Referencias
- Fite, 1921, p. 20
- Even if the 3 is thought of as a constant polynomial so that this could be considered a factorization into polynomials.
- González -Mancil. Álgebra elemental moderna
- Piskunov. Cálculo diferencial e integral
- Sanford, Vera (2008) [1930], A Short History of Mathematics, Read Books, ISBN 9781409727101.
- Fite, 1921, p. 19
- Burnside y Panton, 1960, p. 38
- Dickson, 1922, p. 27
- Stover, Christopher AC Method - Mathworld
- Selby, 1970, p. 101
- En estos campos 2 = 0 por lo que la división en la fórmula no es válida. Hay otras maneras de encontrar las raíces de ecuaciones cuadráticas más de estos campos.
- «Descomposición como Producto de Potencias de Números Primos». Mates fácil. Consultado el 24 de noviembre de 2020.
Bibliografía
- Weisstein, Eric W. «Factorización». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Factor». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Enlaces externos
 Wikiversidad alberga proyectos de aprendizaje sobre Factorización.
Wikiversidad alberga proyectos de aprendizaje sobre Factorización.- WIMS Factoris es un recurso en línea para factoreo numérico, (en inglés)
- Online Factorizer, recurso en línea para factoreo numérico, (en inglés)