Ecuación de Hammett

La ecuación de Hammett, en química orgánica, describe la relación lineal de energía libre relativa a la velocidad de reacción y la constante de equilibrio de varias reacciones que involucran a los derivados del ácido benzoico con sustituyentes meta- y para- entre sí con dos parámetros: una constante de sustituyente y una constante de reacción.[1][2] Esta ecuación fue desarrollada y publicada por Louis Plack Hammett en 1937[3] como un seguimiento de las observaciones cualitativas de una publicación de 1935.[4]

Desarrollo de la ecuación

La idea básica es que para dos reacciones cualesquiera con dos reactivos aromáticos que solo difieren en el tipo de sustituyente, el cambio en la energía de activación es proporcional al cambio de su energía libre de Gibbs.[5] Esta noción, que no se deriva de la termoquímica o de la cinética química, fue introducida por Hammett intuitivamente.[nota 1] La ecuación básica es:

que relaciona la constante de equilibrio, K, para una reacción en equilibrio dada con un sustituyente R, y la constante de referencia K0 cuando R es un átomo de hidrógeno, para una constante de sustituyentes σ que solo depende del sustituyente específico R y de la constante de reacción ρ, dependiendo esta última del tipo de reacción pero no del sustituyente utilizado. La ecuación también puede expresarse en función de las constantes de velocidad de reacción, k, de una serie de reacciones con derivados de sustituyentes del benceno:

En esta ecuación k0 es la constante de velocidad de referencia para reactivos no sustituidos, y k la del reactivo sustituyente. Una gráfica de log(K/K0) para un equilibrio dado versus log(k/k0) para una reacción dada con diferentes sustituyentes da una relación lineal.

Modificaciones posteriores

Otras ecuaciones actuales que refinan el concepto original de la ecuación son:

  • La ecuación de Swain-Lupton, que incluye include tanto los efectos inductivos como los efectos de resonancia en la ecuación.[6]
  • La ecuación de Taft, que modifica la ecuación de Hammett al también describir los efectos estéricos de un sustituyente.[7]
  • La ecuación de Grunwald-Winstein, en el que se tiene en cuenta los efectos del disolvente como nucleófilo.[8][9]
  • La ecuación de Yukawa-Tsuno, que modifica la ecuación para dar cuenta de los efectos de resonancia mejorados en las reacciones electrofílicas de los compuestos orgánicos para- y meta- sustituidos.[10]

También se desarrolló, en 2002, una ecuación que aborda la estereoquímica en sistemas alifáticos, enfrentando sustituyentes polares ecuatoriales con sustituyentes axiales.[11]

Variables de la ecuación

Constante de los sustituyentes
Constantes para sustituyentes para vs meta[3]
SustituyenteEfecto para-Efecto meta-
Dimetilamino-0.83-0.211
Amino-0.66-0.161
Metoxi-0.268+0.115
Etoxi-0.25+0.015
Metil-0.170-0.069
Ninguno0.0000.000
Flúor+0.062+0.337
Cloro+0.227+0.373
Bromo+0.232+0.393
Iodo+0.276+0.353
Ciano+0.66+0.56
Nitro+0.778+0.710

El punto de inicio para la recolección de las constantes sustituyentes es el equilibrio químico tanto para la constante del sustituyente como para la constante de reacción que se establecen arbitrariamente en 1: la ionización del ácido benzoico (R y R' ambos H) en agua a 25 °C.

Scheme 1. Disociación de ácidos benzoicos

Para cada valor obtenido de K0se determinan una serie de constantes de equilibros (K) básandose en el mismo proceso, pero ahora con la variación de los sustituyentes para -por ejemplo, el ácido p-hidroxibenzoico (R=OH, R'=H) o el ácido 4-aminobenzoico (R=NH2, R'=H). De estos valores, combinados en la ecuación de Hammett con K0 y recordando que ρ = 1,se obtiene la constante de sustituyente para. Repitiendo el proceso con sustituyentes meta se obtiene la constante de sustituyente metas. Este tratamiento no incluye sustituyentes orto-, los cuales pueden introducir efectos estéricos.

Los valores de σ reflejados en la tabla[nota 2] revelan ciertos efectos de los sustituyentes. Para ρ = 1, el grupo de sustituyentes con incremento positivo de los valores -notablemente los grupos ciano y nitro causa que la constante de equilibrio aumente en comparación con la referencia del hidrógeno, significando que la acidez del ácido carboxílico (representado a la izquierda de la ecuación) ha aumentado. Estos sustituyentes estabilizan la carga negativa en el átomo de oxígeno del carboxilo por un efecto inductor de electrones (-I) y también por un efecto mesomérico negativo (-M).[12]

El siguiente conjunto de sustituyente son los halógenos, para los cuales el efecto del sustituyente es aún positivo pero mucho más modesto. La razón de esto es que mientras el efecto inductivo es todavía negativo, el efecto mesomérico es positivo, causando una cancelación parcial. Los datos también demuestran que para esos sustituyentes, el efecto meta es mucho más grande que el efecto para, debido al hecho de que el efecto mesomérico se reduce en gran medida en un sustituyente meta. Con los sustituyentes metas un átomo de carbono teniendo la carga negativa está más lejos del grupo ácido carboxílico.

Este efecto se refleja en el siguiente esquema, donde, para un areno sistuido 1a, una estructura resonante 1b es una quinona con carga positiva en el sustituyente X, liberando electrones y por lo tanto desestabilizando el sustituyente Y. Este efecto desestabilizador no es posible cuando X tiene una orientación meta.

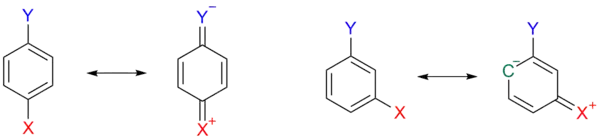
Scheme 3. Hammett Inductive Mesomeric Effects
Scheme 3. Hammett Inductive Mesomeric Effects

Otros sustituyentes, como el metoxi o el etoxi, incluso puede tener signos opuestos para la constante del sustituyente como resultado del efecto inductivo y mesomérico opuesto. Solo los sustituyentes alquilo y arilo como el metilo son liberadores de electrones en ambos aspectos. Cuando el signo de la constante de la reacción sea negativa, solo los sustituyentes cuya constante sea también negativa experimentarán un aumento de las constantes de equilibrio.

Constante de la reacción

Conociendo las constante de los sustituyentes es posible obtener las constantes de las reacciones para un gran rango de reacciones orgánicas. La reacción arqueotipo es la hidrólisis alcalina del benzoato de etilo (R = R' = H) en una mezcla de agua y etanol a 30 °C. Medidas de la velocidad de reacción combinadas con la de muchos benzoatos de etilo sustituidos, en última instancia, se obtiene una constante de reacción de +2.498.[3]

Scheme 2. Hydrolysis of benzoic acid esters
Scheme 2. Hydrolysis of benzoic acid esters

Las constantes de reacción son conocidas por muchas otras reacciones y equilibrios. La constante de reacción o constante de sensibilidad, ρ, describe la susceptibilidad de la reacción a los sustituyentes, en comparación con la ionización del ácido benzoico. Es equivalente a la pendiente de la gráfica de Hammett. La información sobre la reacción y el mecanismo asociado pueden obtenerse sobre la base del valor obtenido para ρ. Los valores de esta constante se pueden clasificar en función de:

  1. ρ>1, la reacción es más sensible a sustituyentes que el ácido benzoico y se genera carga negativa durante la reacción (o se pierde carga positiva).
  2. 0<ρ<1, la reacción es menos sensible a sustituyentes que el ácido benzoico y se genera carga negativa durante la reacción (o se pierde carga positiva).
  3. ρ=0, no hay sensibilidad a los sustituyentes, y no se crea ni se pierde ninguna carga.
  4. ρ<0, la reacción construye carga positiva (o pierde carga negativa).

Estas relaciones pueden ser explotadas para elucidar el mecanismo de la reacción. Como el valor de ρ está relacionado con la carga durante el paso limitante de la velocidad, los mecanismos se pueden diseñar en base a esta información. Si se piensa que el mecanismo para la reacción de un compuesto aromático se produce a través de uno de dos mecanismos, el compuesto puede modificarse con sustituyentes con diferentes valores de "σ" y medidas cinéticas tomadas. Una vez que se han realizado estas mediciones, se puede construir un diagrama de Hammett para determinar el valor de ρ. Si uno de estos mecanismos implica la formación de carga, esto puede verificarse en función del valor ρ. Por el contrario, si el gráfico de Hammett muestra que no se desarrolla ninguna carga, es decir, una pendiente cero, el mecanismo que implica la construcción de carga puede descartarse.

Los gráficos de Hammett pueden no ser siempre perfectamente lineales. Por ejemplo, una curva puede demostrar un cambio repentino en la pendiente, o constante ρ. En tal caso, es probable que el mecanismo de la reacción cambie al agregar un sustituyente diferente. Otras desviaciones de la linealidad pueden deberse a un cambio en la posición del estado de transición. En tal situación, ciertos sustituyentes pueden hacer que el estado de transición aparezca antes (o más tarde) en el mecanismo de reacción.[13]

Efectos electrónicos dominantes

Predominan 3 tipos de estado fundamental o influencias eléctricas estáticas:

  • Efecto de resonancia mesomérico.
  • Efecto inductivo: influencia eléctrica de un grupo que se transmite principalmente por polarización de los electrones de unión de un átomo al siguiente.
  • Efecto electroestático directo: influencia eléctrico de un sustituyente polar o dipolar el cual es transmitido primariamente al grupo reactivo a través del espacio (incluyendo disolvente, si lo hay) acorde a las leyes clásicas de la electroestática.

Las últimas dos influencias suelen ser tratadas como un efecto compuesto, pero pueden ser tratadas separadamente. Westheimer demostró que los efectos eléctricos de los grupos dipolos π-sustituidos en la acidez del ácido benzoico y fenilacético puede ser cuantitativamente correlaccionado, al asumir solo la acción electrostática directa del sustituyente sobre el protón ionizable del grupo carboxílico. El tratamiento de Westheimer funcionó bien excepto aquellos ácidos con sustituyentes que tienen pares de electrones no compartidos como el -OH y el -OCH3, ya que estos sustituyentes interactúan fuertemente con el anillo del benceno.[14][15]

Ácido biciclo[2.2.2]octano-1-carboxílico 4-sustituido

Roberts y Moreland estudió la reactividad del ácido biciclo[2.2.2]octano-1-carboxílico 4-sustituido y sus ésteres. En una molécula de este tipo, no es posible la transmisión de efectos eléctricos de sustituyentes a través del anillo por resonancia. Por lo tanto, esto insinúa el papel de los electrones π en la transmisión de los efectos de los sustituyentes a través de los sistemas aromáticos.[16]

La reactividad de los ácidos biciclo[2.2.2]octano-1-carboxílico 4-sustituido y sus ésteres fueron medidos en 3 procesos diferentes, cada uno de los cuales se había usado previamente con derivados del ácido benzoico. Una gráfica de log(k) frente log(KA) muestra una relación lineal. Tales relaciones lineales corresponden a relaciones lineales de energía libre, que implican fuertemente que el efecto de los sustituyentes se ejerce a través de cambios de potencial de energía y que los términos estéricos y entrópicos permanecen casi constantes a través de la serie. La relación lineal encaja bien en la ecuación de Hammett. Para los derivados del ácido biciclo[2.2.2]octano-1-carboxílico 4-sustituido, las constantes de sustituyentes y de reacción son designados como σ’ y ρ’, respectivamente.

Si comparamos ρ con ρ’, los datos de reactividad indican que los efectos de los grupos sustituyentes en determinar la reactividad de los sustituyentes del ácido benzoico y del ácido biciclo[2.2.2]octano-1-carboxílico son comparables. Esto implica que los electrones π del anillo aromático no juegan un importante papel en la transmisión de los efectos electrónicos en grupos dipolares al grupo carboxilo ionizable. Las diferencias entre ρ y ρ’ para las reacciones de los ácidos con difenilazometano es probablemente debido a una relación inversa con la constante dipolar De del disolvente.[16]

Al comparar σ con σ’, para grupos meta- directores (grupo atractores de electrones o EWG por sus siglas en inglés) σmeta y σpara son más positivos que σ’. Para grupos orto-para- directores (grupos dadores de electrones o EDG por sus siglas en inglés), es más positivo que σmeta and σpara. Las diferencia entre σpara y σ’ () es mayor que entre σ meta and σ’. Esto es esperable ya que los efectos de resonancia electrónica se sienten con mayor fuerza en las posiciones para. Los valores (σ – σ’) pueden ser tomados como una medida razonable de los efectos de resonancia.

No linealidad

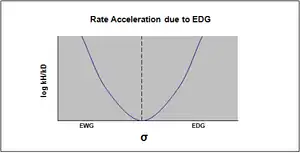
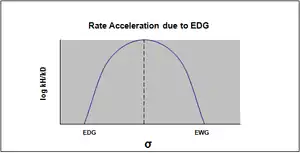
La gráfica de la ecuación de Hammett es comúnmente vista como lineal, con una pendiente positiva o negativa que se correlaciona con el valor de ρ. Sin embargo, la no linealidad emerge en la gráfica de Hammett cuando un sustituyente afecta la velocidad de reacción o cambia la etapa limitante o el mecanismo de la reacción. Por la razón del primer caso, se introducen nuevas constantes σ para acomodar la desviación de la linealidad vista de otro modo como resultado del efecto del sustituyente.

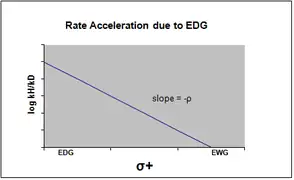
σ+ tiene en cuenta la acumulación de carga positiva que se produce en el estado de transición de la reacción. Por lo tanto, un grupo dador de electrones (EDG) acelerará la velocidad de la reacción mediante estabilización de resonancia y dará la siguiente gráfica σ con un valor de ρ negativo.[17]

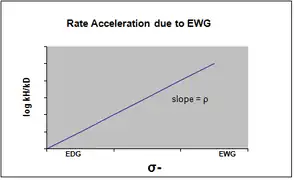
σ- se designa en el caso en que se produce una acumulación de carga negativa en el estado de transición, y la velocidad de reacción se acelera en consecuencia por grupos atractores de electrones (EWG). El grupo atractor de electrones retira la densidad de electrones por resonancia y estabiliza efectivamente la carga negativa que se genera. La gráfica correspondiente mostrará un valor de ρ positivo.

Tasa de aceleración debido a grupos dadores de electrones (EDG)
Tasa de aceleración debido a grupos dadores de electrones (EDG)  
Tasa de aceleración debido a grupos atractores de electrones (EWG)
Tasa de aceleración debido a grupos atractores de electrones (EWG)  

En el caso de una sustitución nucleófila acílica el efecto del sustituyente, X, del grupo no saliente puede de hecho acelerar la velocidad de la reacción de adición nucleofílica cuando X es un grupo atractor de electrones. Esto se atribuye a la contribución de resonancia del grupo atractor de electrones para retirar la densidad de electrones, lo que aumenta la susceptibilidad al ataque nucleofílico del carbono carbonílico. Se produce un cambio en la velocidad cuando X es EDG, como se evidencia al comparar las tasas entre X = Me y X = OMe, y se observa la no linealidad en la gráfica de Hammett.[18]

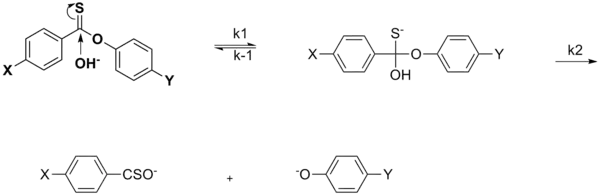
Nucleophilic acyl substitution
Nucleophilic acyl substitution

El efecto del sustituyente puede cambiar la etapa limitante de velocidad en el mecanismo de la reacción. Un cierto efecto electrónico puede acelerar cierto paso para que ya no sea la etapa limitante.[19]

Un cambio en el mecanismo de una reacción resulta en una gráfica de Hammett no lineal. Por lo general, el modelo utilizado para medir los cambios en la velocidad en este caso es el de la reacción SN2.[20] Sin embargo, se ha observado que en algunos casos de una reacción SN2 que un grupo atractor de electrones no acelera la reacción como se esperaría.[21] y que la tasa varía con el sustituyente. De hecho, el signo de la carga y el grado al que se desarrolla se verá afectado por el sustituyente en el caso del sistema bencílico.[20]

Por ejemplo, el sustituyente puede determinar que el mecanismo sea una reacción tipo SN1 sobre una reacción tipo SN2,en cuyo caso, el gráfico resultante de Hammet indicará una aceleración de velocidad debida a un grupo dador de electrones, aclarando así el mecanismo de la reacción. Otra desviación de la ecuación regular de Hammett se explica por la carga de nucleófilo.[20] A pesar de la no linealidad en las reacciones bencílicas de las SN2, los grupos atractores de electrones podrían acelerar o retardar la reacción. Si el nucleófilo está cargado negativamente (por ejemplo, el cianuro) el grupo atractor de electrones aumentará la velocidad debido a la estabilización de la carga adicional que se aplica al carbono en el estado de transición. Por otro lado, si el nucleófilo no está cargado (como el grupo trifenilfosfina), los grupos dadores de electrones va a ralentizar la reacción al disminuir la densidad de electrones en el orbital antienlazado del grupo saliente en el estado de transición.

Cambio en el mecanismo de la reacción
Cambio en el mecanismo de la reacción  
Cambio en la etapa limitante de velocidad
Cambio en la etapa limitante de velocidad  

Véase también

Notas
  1. En la línea inicial de su publicación de 1935, Hammett escribe:
    La ides de que hay algunos tipo de relación entre la velocidad de una reacción y la constante de equilibrio es uno de los conceptos más persistentemente retenidos y al mismo tiempo más enfáticamente negados en la teoría química.
  2. Estos valores son los valores originales obtenidos por Hammett en su publicación de 1937, y pueden diferir de publicaciones posteriores enviadas por otras personas. El siguiente enlace contiene constante de sustituyentes comúnmente aceptados: C. Hansch, A. Leo and R. W. Taft (1991). «A survey of Hammett substituent constants and resonance and field parameters». Chem. Rev. 91 (2): 165-195. doi:10.1021/cr00002a004.

Referencias
  1. Unión Internacional de Química Pura y Aplicada. «{{{title}}}». Compendium of Chemical Terminology. Versión en línea (en inglés).
  2. Keenan, Sheue L.; Peterson, Karl P.; Peterson, Kelly; Jacobson, Kyle (2008). «Determination of Hammett Equation Rho Constant for the Hydrolysis of p-Nitrophenyl Benzoate Esters». J. Chem. Educ. 85 (4): 558. Bibcode:2008JChEd..85..558K. doi:10.1021/ed085p558.
  3. Hammett, Louis P. (1937). «The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives». J. Am. Chem. Soc. 59 (1): 96. doi:10.1021/ja01280a022.
  4. Louis P. Hammett (1935). «Some Relations between Reaction Rates and Equilibrium Constants». Chem. Rev. 17 (1): 125-136. doi:10.1021/cr60056a010.
  5. Advanced Organic Chemistry Part A Second Edition F.A. Carey, R.J. Sundberg Plenum Press ISBN 0-306-41198-9
  6. Swain, C. Gardner; Lupton, Elmer C. (1968). «Field and resonance components of substituent effects». publicación of the American Chemical Society 90 (16): 4328-4337. doi:10.1021/ja01018a024.
  7. Hansch, Corwin; Leo, A.; Taft, R. W. (1991). «A survey of Hammett substituent constants and resonance and field parameters». Chemical Reviews 91 (2): 165-195. doi:10.1021/cr00002a004..
  8. Anslyn, Eric V.; Dougherty, Dennis A. (2006). University Science Books, ed. Modern Physical Organic Chemistry (en inglés). p. 456. ISBN 1891389319. (requiere registro).
  9. Catalán, Javier; Díaz, Cristina; García-Blanco, Francisco (1999). «Correlation of Solvolysis Rates 50 años Later». The publicación of Organic Chemistry 64 (17): 6512-6514. doi:10.1021/jo990588w.
  10. Yukawa, Yasuhide; Tsuno, Yuho; Sawada, Masami (1966). «Resonance effect in Hammett relationship. IV. Linear free energy relationship based on the normal substituent constant». Bulletin of the Chemical Society of Japan 39 (10): 2274-2286. doi:10.1246/bcsj.39.2274.
  11. Bols, Mikael; Liang, Xifu; Jensen, Henrik H. (2002). «Equatorial contra axial polar substituents. The relation of a chemical reaction to stereochemical substituent constants». J. Org. Chem. 67 (25): 8970. doi:10.1021/jo0205356.
  12. Sykes, Peter (1985). Mecanismos de reacción en Química Orgánica. Editorial Reverté. p. 358-359. ISBN 84-291-7504-0.
  13. E.V. Anslyn & D.A. Dougherty, Modern Physical Organic Chemistry, pp. TBD, Sausalito, CA, US: University Science Books, ISBN 1891389319
  14. Westheimer F.H. (1939). «The Electrostatic effect of substituents on the dissociation constants of organic acids. IV. Aromatic acids». J. Am. Chem. Soc. 61 (8): 1977. doi:10.1021/ja01877a012.
  15. Kirkwood J.G.; Westheimer F.H. (1938). «The electrostatic influence of substituents on the dissociation constants of organic acids. I [Missing Subtítulo]». J. Chem. Phys. 6 (9): 506. Bibcode:1938JChPh...6..506K. doi:10.1063/1.1750302.
  16. Roberts J.D.; Moreland Jr. W.T. (1953). «Electrical Effects of Substituent Groups in Saturated Systems. Reactivities of 4-Substituted Bicyclo [2.2.2] octane-1-carboxylic acids». J. Am. Chem. Soc. 75 (9): 2167-2173. doi:10.1021/ja01105a045.
  17. Y. Yukawa & Y. Tsuno, 1959, "Resonance Effect in Hammett Relationship. II. Sigma Constants in Electrophilic Reactions and their Intercorrelation," Bull. Chem. Soc. Jpn. 32:965-971, see , accessed 22 June 2015.
  18. Um, Ik-Hwan; Lee, Ji-Youn; Kim, Han-Tae; Bae, Sun-Kun (2004). «Curved Hammett plot in alkaline hydrolysis of O-aryl thionobenzoates: Change in rate-determining step versus ground-state stabilization». J. Org. Chem. 69 (7): 2436-2441. doi:10.1021/jo035854r.
  19. Hart, H.; Sedor, Edward A. (1967). «Mechanism of cyclodehydration of 2-phenyltriarylcarbinols». J. Am. Chem. Soc. 89 (10): 2342. doi:10.1021/ja00986a018.
  20. Stein, Allan R.; Tencer, Michal; Moffatt, Elizabeth A.; Dawe, Robert; Sweet, James (1980). «Nonlinearity of Hammett .sigma..rho. correlations for benzylic systems: activation parameters and their mechanistic implications». J. Org. Chem. 45 (17): 3539-3540. doi:10.1021/jo01305a045. Consultado el 22 de junio de 2015.
  21. Young, P. R.; Jencks, W. P. (1979). «Separation of polar and resonance substituent effects in the reactions of acetophenones with bisulfite and of benzyl halides with nucleophiles». J. Am. Chem. Soc. 101 (12): 3288. doi:10.1021/ja00506a025.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.