Constante de disociación ácida
Una constante de disociación ácida, Ka, (también conocida como constante de acidez, o constante de ionización ácida) es una medida cuantitativa de la fuerza de un ácido en disolución. Es la constante de equilibrio de una reacción conocida como disociación en el contexto de las reacciones ácido-base. El equilibrio puede escribirse simbólicamente como:
- HA
 A- + H+
A- + H+

donde HA es un ácido genérico que se disocia dividiéndose en A-, conocida como base conjugada del ácido, y el ion hidrógeno o protón, H+, que, en el caso de soluciones acuosas, existe como un ion hidronio solvatado. En el ejemplo que se muestra en la figura, HA representa el ácido acético, y A- el ion acetato. Las especies químicas HA, A- y H+ se dice que están en equilibrio cuando sus concentraciones no cambian con el paso del tiempo. La constante de disociación se escribe normalmente como un cociente de las concentraciones de equilibrio (en mol/L), representado por [HA], [A-] y [H+]:
Debido a los muchos órdenes de magnitud que pueden abarcar los valores de K a, en la práctica se suele expresar la constante de acidez mediante una medida logarítmica de la constante de acidez, el pKa, que es igual al -log10, y que también suele ser denominada constante de disociación ácida:
A mayor valor de pKa, la extensión de la disociación es menor. Un ácido débil tiene un valor de pKa en un rango aproximado de 2 a 12 en agua. Los ácidos con valores de pKa menores que aproximadamente 2 se dice que son ácidos fuertes; un ácido fuerte está casi completamente disociado en solución acuosa, en la medida en que la concentración del ácido no disociado es indetectable. Los valores de pKa para los ácidos fuertes pueden ser estimados por medios teóricos o por extrapolación de medidas en medios no acuosos, en los que la constante de disociación es menor, tales como acetonitrilo y dimetilsulfóxido.
Introducción
La constante de disociación ácida es una consecuencia directa de la termodinámica subyacente a la reacción de disociación, el valor de pKa es directamente proporcional al cambio de energía libre de Gibbs estándar para la reacción. El valor de pKa cambia con la temperatura y se puede entender de forma cualitativa en base al principio de Le Châtelier: cuando la reacción es endotérmica, el valor de pKa disminuye con el aumento de temperatura, lo contrario es cierto para las reacciones exotérmicas. Los factores estructurales subyacentes que influyen en la magnitud de la constante de disociación ácida incluyen las reglas de Pauling para las constantes de acidez, los efectos inductivos, los efectos mesoméricos, y el enlace por puente de hidrógeno.
El comportamiento cuantitativo de los ácidos y bases en solución solo puede ser comprendido si se conocen los valores de pKa. En particular, el pH de una solución se puede predecir cuando se conocen la concentración analítica y los valores de pKa de todos los ácidos y las bases; inversamente, también es posible calcular las concentraciones de equilibrio de los ácidos y sus bases en solución cuando se conoce el pH. Estos cálculos tienen aplicación en diferentes áreas de la química, la biología, la medicina y la geología. Por ejemplo, muchos de los compuestos utilizados para la medicación son ácidos o bases débiles, y el conocimiento de los valores de pKa, junto con el coeficiente de reparto octanol-agua, puede utilizarse para estimar la medida en que el compuesto entra en el torrente sanguíneo.
Las constantes de disociación ácida también son esenciales en química en disolución acuosa y oceanografía química, donde la acidez del agua juega un papel fundamental. En los organismos vivos, la hemostasis ácido-base y la cinética enzimática son dependientes de los valores de pKa de muchos de los ácidos y bases presentes en la célula y en el cuerpo.
En química, es necesario el conocimiento de los valores de pKa para la preparación de soluciones tampón, y también es un requisito previo para la comprensión cuantitativa de la interacción entre los ácidos o las bases y los iones metálicos para formar complejos. Experimentalmente, los valores de pKa pueden determinarse por valoración potenciométrica (pH), pero para valores de pKa menores que aproximadamente 2 o aproximadamente mayores de 11, pueden requerirse medidas espectrofotométricas o de RMN debido a las dificultades prácticas con las medidas de pH.
Definiciones
De acuerdo con la definición original de Arrhenius, un ácido es una sustancia que se disocia en solución acuosa, liberando el ion hidrógeno H+ (un protón):[1]
- HA
 A- + H+
A- + H+
La constante de equilibrio para esta reacción de disociación se conoce como constante de disociación. El protón liberado se combina con una molécula de agua para dar un (ion hidronio o oxonio) H3O+, y así más tarde Arrhenius propuso que la disociación se debe escribir como una reacción ácido-base:
- HA + H2O
 A- + H3O+
A- + H3O+
La Teoría de Brønsted–Lowry generaliza esto algo más al considerarla como una reacción de intercambio de protones:[2][3][4]
- ácido + base
 base conjugada + ácido conjugado
base conjugada + ácido conjugado
El ácido pierde un protón, dando la base conjugada, el protón se transfiere a la base, dando el ácido conjugado. Para soluciones acuosas de un ácido HA, la base es el agua, la base conjugada del ácido es A- y el ácido conjugado de la base es el ion hidronio. La definición de Brønsted-Lowry se aplica a otros disolventes, como el dimetilsulfóxido: el solvente S actúa como una base, aceptando un protón y formando el ácido conjugado SH+.
En química en solución es común utilizar H+ como una abreviatura del ion hidrógeno solvatado, independientemente del disolvente. En solución acuosa, H+ denota un ion hidronio solvatado en lugar de un protón.[5][6]
La designación de un ácido o una base como "conjugado" depende del contexto. El ácido conjugado BH+ de una base B se disocia según la ecuación:
- BH+ + OH-
 B + H2O
B + H2O
que es la inversa del equilibrio:
- H2O (ácido) + B (base)
 OH− (base conjugada) + BH+ (ácido conjugado)
OH− (base conjugada) + BH+ (ácido conjugado)
El ion hidróxido OH−, una base bien conocida, actúa aquí como la base conjugada del ácido agua. Los ácidos y las bases se consideran así simplemente como donadores o aceptores de protones, respectivamente.
El agua es anfiprótica: puede reaccionar tanto como un ácido o como una base. Otro ejemplo de molécula anfiprótica es el ion bicarbonato HCO3- que es la base conjugada del ácido carbónico H2CO3 en el equilibrio:
- H2CO3 + H2O
 HCO3- + H3O+
HCO3- + H3O+
pero también el ácido conjugado del ion carbonato CO32- en la reacción inversa del equilibrio:
- HCO3- + OH-
 CO32- + H2O
CO32- + H2O
El equilibrio del ácido carbónico es importante para la homeostasis ácido-base en el cuerpo humano.
Una definición más amplia de la disociación ácida incluye la hidrólisis, en la que los protones son producidos por la separación de moléculas de agua. Por ejemplo, el ácido bórico (B(OH)3) actúa como un ácido débil, aunque no es un donante de protones, debido a la hidrólisis:
- B(OH)3 + 2 H2O
 B(OH)4- + H3O+
B(OH)4- + H3O+
Del mismo modo, la hidrólisis de los iones metálicos produce iones como el [Al(H2O)6]3+ que se comportan como ácidos débiles:[7]
- [Al(H2O)6]3+ + H2O
 [Al(H2O)5(OH)]2+ + H3O+
[Al(H2O)5(OH)]2+ + H3O+
Constante de equilibrio
Una constante de disociación ácida es un ejemplo particular de una constante de equilibrio. Para el equilibrio específico entre un ácido monoprótico, HA y su base conjugada A- en agua:
- HA + H2O
 A- + H3O+
A- + H3O+
la constante de equilibrio termodinámica, K![]() puede definirse por:[8]
puede definirse por:[8]
donde {A} es la actividad de la especie química A, etc. K![]() es adimensional ya que la actividad no tiene dimensiones . Las actividades de los productos de disociación están colocados en el numerador, las actividades de los reactivos están colocadas en el denominador. Ver coeficiente de actividad para una deducción de esta expresión.
es adimensional ya que la actividad no tiene dimensiones . Las actividades de los productos de disociación están colocados en el numerador, las actividades de los reactivos están colocadas en el denominador. Ver coeficiente de actividad para una deducción de esta expresión.
Puesto que la actividad es el producto de la concentración y el coeficiente de actividad (γ) la definición podría también escribirse como:
donde [HA] representa la concentración de HA y Γ es un cociente de coeficientes de actividad.

Para evitar las complicaciones que implica el uso de actividades, las constantes de disociación se determinan, cuando es posible, en un medio de alta fuerza iónica, es decir, bajo condiciones en las que Γ se puede suponer que es siempre constante.[8] por ejemplo, el medio puede ser una solución de 0.1 M de nitrato de sodio o 3 M de perclorato de potasio (1 M = 1 mol·dm−3, una unidad de concentración molar). Además, en todos, salvo en las soluciones más concentradas se puede suponer que la concentración de agua, [H2O], es constante, aproximadamente 55 mol·dm−3. Dividiendo K![]() por los términos constantes y escribiendo [H+] para la concentración de hidronio, se obtiene la expresión:
por los términos constantes y escribiendo [H+] para la concentración de hidronio, se obtiene la expresión:
Esta es la definición de uso común.[9] pKa se define como -log10Ka. Nótese, sin embargo, que todos los valores de las constantes de disociación publicados se refieren al medio iónico específico utilizado en su determinación y que se obtienen diferentes valores con distintas condiciones, como se muestra para ácido acético en la ilustración anterior. Cuando las constantes publicadas se refieren a una fuerza iónica que no sea la requerida para una aplicación particular, puede ajustarse mediante la teoría de iones específicos (SIT) y otras teorías.[10]
AunqueKa parece tener la dimensión de concentración, de hecho, debe ser adimensional o no sería posible obtener su logaritmo. La ilusión es el resultado de omitir el término constante [H_2O] de la definición de la expresión. Sin embargo, no es inusual, sobre todo en textos relativos a equilibrios bioquímicos, ver un valor citado con una dimensión como, por ejemplo, "Ka = 300 M".
Ácidos monopróticos
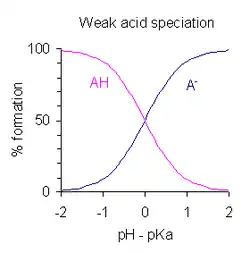
Después de modificar la expresión que define Ka tomando logaritmos y poniendo pH =-log 10 [H+] se obtiene:
Esta es una forma de la ecuación de Henderson-Hasselbalch, de la que pueden obtenerse las siguientes conclusiones:
- A mitad de la neutralización [AH]/[A-] = 1; dado que log (1) = 0, el pH a mitad de la neutralización es numéricamente igual al pKa. Inversamente, cuando el pH = pKa, la concentración de AH es igual a la concentración de A-.
- La región tamponada se extiende sobre el intervalo aproximado pKa ± 2, aunque el tamponamiento es débil fuera del rango de pKa ± 1. Cuando pKa ± 1, entonces [AH]/[A-] = 10 o 1/10.
- Si se conoce el pH, se puede calcular la relación [AH]/[A-]. Esta relación es independiente de la concentración analítica del ácido.
En el agua, los valores medibles de pKa varían en un rango que va desde alrededor de -2 para un ácido fuerte a cerca de 12 para un ácido muy débil (o base fuerte). Todos los ácidos con un valor de pKa menores que -2 están disociados más del 99 % a un pH de 0 (1 M de ácido). Esto se conoce como efecto nivelador del disolvente ya que todos los ácidos parecen estar al mismo nivel de ácidos fuertes, independientemente de sus valores de pKa. Asimismo, todas las bases con un valor de pKa mayor que el límite superior están desprotonadas en más del 99 % para todos los valores posibles de pH y se clasifican como bases fuertes.[3]
Un ejemplo de ácido fuerte es el ácido clorhídrico, HCl que tiene un valor de pKa, estimado a partir de medidas termodinámicas de -9,3 en agua.[11] La concentración de ácido no disociado en una solución 1 mol·dm−3 sería menor del 0.01 % de las concentraciones de los productos de disociación. Se dice que el ácido clorhídrico está completamente disociado en solución acuosa porque la cantidad de ácido no disociado es imperceptible. Cuando se conocen el pKa y la concentración analítica del ácido, se puede calcular fácilmente la extensión de la disociación y el pH de una solución de un ácido monoprótico utilizando una tabla ICE (concentraciones iniciales, cambio y concentraciones en el equilibrio).
Un tampón de un pH deseado puede prepararse como una mezcla de un ácido débil y su base conjugada. En la práctica, la mezcla puede crearse disolviendo el ácido en agua, y agregando la cantidad necesaria de ácido o base fuerte. El pKa del ácido debe ser inferior a dos unidades de diferencia del pH de destino.
Ácidos polipróticos
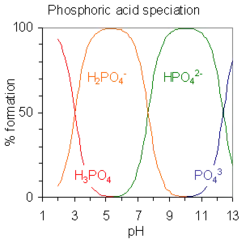
Los ácidos polipróticos son ácidos que pueden perder más de un protón. La constante de disociación para el primer protón puede indicarse como Ka1 y las constantes de disociación de los sucesivos protones como Ka2, etc. El ácido fosfórico, H3PO4, es un ejemplo de ácido poliprótido que puede perder tres protones.
equilibrio Valor de pKa H3PO4  H2PO4− + H+
H2PO4− + H+pKa1 = 2.15 H2PO4−  HPO42− + H+
HPO42− + H+pKa2 = 7.20 HPO42−  PO43− + H+
PO43− + H+pKa3 = 12.37
Cuando la diferencia entre valores sucesivos de pK es de alrededor de cuatro o más unidades, como en este ejemplo, cada especie puede considerarse como un ácido por derecho propio.[12] De hecho, las sales de H2PO4− pueden cristalizarse de una solución ajustando el pH alrededor de 5.5 y las sales de HPO42− pueden cristalizarse de la solución ajustando el pH alrededor de 10. El diagrama de distribución de especies muestra que las concentraciones de los dos iones son máximas a pH 5.5 y 10.
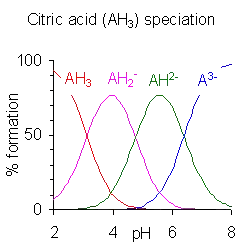
Cuando la diferencia entre valores sucesivos de pK es menor que aproximadamente cuatro hay superposición entre el rango de pH de existencia de las especies en equilibrio. A menor diferencia, mayor solapamiento. El caso del ácido cítrico se muestra a la derecha; las soluciones de ácido cítrico están tamponadas en el rango completo de pH de 2,5 a 7,5.
En general, es cierto que los sucesivos valores de pK aumentan (Primera regla de Pauling).[13] por ejemplo, para un ácido diprótico, H2A, los dos equilibrios son:
- H2A
 HA− + H+
HA− + H+ - HA−
 A2− + H+
A2− + H+
se puede observar que el segundo protón se retira de una especie cargada negativamente. Dado que el protón tiene una carga positiva se necesita un trabajo extra para arrancarlo; esta es la causa de la tendencia señalada anteriormente. Los (anteriores) valores para el ácido fosfórico ilustran esta regla, al igual que los valores del ácido vanádico, H3VO4. Cuando se encuentra una excepción a la regla indica que está ocurriendo un cambio importante en la estructura. En el caso de VO2+ (aq), el vanadio tiene geometría molecular octaédrica, (número de coordinación 6), mientras que el ácido vanádico tiene geometría molecular tetraédrica, (número de coordinación 4). Esta es la explicación de porqué pKa1 > pKa2 para los oxoácidos de vanadio (V).
equilibrio Valor de pKa [VO2(H2O)4]+  H3VO4 + H+ + 2H2O
H3VO4 + H+ + 2H2OpKa1 = 4.2 H3VO4  H2VO4− + H+
H2VO4− + H+pKa2 = 2.60 H2VO4−  HVO42− + H+
HVO42− + H+pKa3 = 7.92 HVO42−  VO43− + H+
VO43− + H+pKa4 = 13.27
Autoionización del agua DPPE&DVPE
El agua tiene propiedades tanto ácidas como básicas. La constante de equilibrio para el equilibrio:
- 2 H2O
 OH− + H3O+
OH− + H3O+
viene dada por:
Cuando, como suele ser usual, la concentración de agua se puede considerar constante, esta expresión puede reemplazarse por:
El valor de Kw en condiciones estándar es 1.0×10−14. La constante de autoionización del agua, Kw, es por tanto, un caso especial de constante de disociación ácida.
Bases
Históricamente, la constante de equilibrio Kb para una base se ha definido como la constante de asociación para la protonación de la base, B, a la forma ácida conjugada, HB+. Normalmente se obtiene a partir del valor de Ka.
- B + H2O
 HB+ + OH−
HB+ + OH−
Utilizando un razonamiento similar al usado anteriormente:
En agua, la concentración del ion hidróxido, [OH−], se relaciona con la concentración del ion hidrógeno mediante Kw = [H+] [OH−], por tanto:
La sustitución de la expresión de [OH−] en la expresión de Kb da:
Cuando Ka, Kb y Kw se determinan en las mismas condiciones de temperatura y fuerza iónica, se sigue, tomando logaritmos que pKb = pKw - pKa. En solución acuosa a 25 °C, pKw es 13.9965,[14] así pKb ~ 14 - pKa. En efecto, no hay necesidad de definir pKb de forma separada de pKa, pero se hace aquí porque los valores de pKb pueden encontrarse en la literatura antigua.
Dependencia de la temperatura
Todas las constantes de equilibrio varían con la temperatura de acuerdo con la ecuación de van't Hoff[15]
R es la Constante universal de los gases ideales y T es la temperatura absoluta . Así, para las reacciones exotérmicas, (el cambio de entalpía estándar, ΔH![]() , es negativo) K disminuye con la temperatura, pero para las reacciones endotérmicas (ΔH
, es negativo) K disminuye con la temperatura, pero para las reacciones endotérmicas (ΔH![]() es positivo) K aumenta con la temperatura.
es positivo) K aumenta con la temperatura.
Acidez en soluciones no acuosas
Clasificación de los disolventes
Un disolvente es una sustancia que permite la dispersión de otra en su seno. De acuerdo con su polaridad los disolventes se pueden clasificar como:
1. Polares. Son sustancias en cuyas moléculas la distribución de la nube electrónica es asimétrica; por lo tanto, la molécula presenta un polo positivo y otro negativo separados por una cierta distancia, por lo que hay un dipolo permanente. El agua es el ejemplo clásico de un disolvente polar. Los disolventes polares se pueden subdividir en:
- Próticos. Contienen un enlace del O-H o del N-H. Ejemplos: Agua (H-O-H), etanol (CH3-CH2-OH) y ácido acético (CH3-COOH) son disolventes polares próticos.
- Apróticos. Este tipo de disolvente no dan ni aceptan protones. La acetona (CH3-CO-CH3), el acetonitrilo, la dimetilformamida o el THF (Tetrahidrofurano) son disolventes polares
2. Disolventes apolares. En general son sustancias de tipo orgánico, en cuyas moléculas la distribución de la nube electrónica es simétrica; por lo que carecen de dipolos permanentes. Dependiendo de la geometría de sus moléculas, si los momentos dipolares individuales de sus enlaces están compensados, la molécula será, en conjunto, apolar. Algunos disolventes de este tipo son: el éter etílico, benceno, tolueno, xileno, cetonas, hexano, ciclohexano y el tetracloruro de carbono.
Sistema de disolvente
La definición de sistema de disolvente aplica a cualquier disolvente que se pueda disociar en un anión y un catión (autodisociación), donde el catión resultante es el ácido y el anión es la base. En agua, la autoionización corresponde a la transferencia de un protón de una molécula de disolvente a otra, siendo un ejemplo de comportamiento anfótero
2 H2O ↔ H3O++ -OH
Donde el catión H3O+ es el ácido y el anión -OH es la base.
Mientras que en NH3 líquido, la transferencia de protones lleva a la formación de [NH4]+, por lo que en una disolución de amoniaco líquido, un ácido puede describirse como una sustancia que produce iones [NH4]+, mientras que una base produce iones [NH2]-
2 NH3 ↔ [NH4]++ [NH2]-
De forma general en un disolvente autodisociado:
- Un ácido es una sustancia que aumenta la concentración del catión característico del disolvente
- Una base es una sustancia que aumenta la concentración del el anión característico del disolvente.
El tamaño de la escala de pH está condiciona por el índice de la constante de autoprotólisis (pKs), la cual es una medida del disolvente para generar in-situm la partícula ácida (catión) y la partícula básica (anión) del disolvente.
Propiedades de algunos disolventes próticos
| Disolvente | Ácida (catión) | Base (anión) | pKs | Punto de ebullición (°C) |
|---|---|---|---|---|
| H2O Agua | H3O+ | -OH | 14 | 100 |
| CH3OH Metanol | CH3OH2+ | CH3O- | 19.52 | 64.7 |
| NH3 Amoniaco | NH4+ | NH2- | 27.7 | -33.4 |
| CH3COOH Ácido acético | CH3COOH2+ | CH3COO- | 10 | 118.2 |
| CH3CN Acetonitrilo | CH3CNH+ | CH3CN- | 28.6 | 81 |
Fuerza relativa de ácidos y bases
La fuerza relativa de los ácidos y las bases se mide en función de la cuantitatividad con la que reaccionan con el disolvente en el que se encuentran. En disolución acuosa la fuerza de un ácido, HA, depende de la capacidad relativa para ceder protones de HA y de H3O+.
- HA + H2O ↔ H3O+ + A-
De forma análoga, la fuerza de una base B, en disolución acuosa depende de la capacidad relativa para aceptar protones de B y -OH
- B + H2O ↔ BH+ + -OH
Los valores de Ka (o Kb) se refieren por lo general a la ionización de ácidos en disolución acuosa y, al decir que “HCl es un ácido fuerte”, se entiende que es en medio acuosos. Sin embargo, si HCl se disuelve en ácido acético (un disolvente más ácido que el agua), su ionización es mucho menor que en agua y por lo que el HCl se comporta como un ácido débil en este disolvente.
Cálculo del pH en disolución en disolventes análogos al H2O [18]
| Tipo de sustancia | Ecuación |
|---|---|
| Ácido fuerte | |
| Ácido débil | |
| Par conjugado | |
| Base fuerte | |
| Base débil | |
En las ecuaciones anteriores, c0 es la concentración formal o analítica, ca la concentración de ácido y cb la concentración de base.
Los disolventes no acuosos que son buenos aceptores de protones (disolventes más básicos que el agua, por ejemplo, NH3), favorecen que los ácidos se ionicen en ellos; de tal forma que en un disolvente básico, todos los ácidos son fuertes; por lo que se dice que el disolvente presenta un efecto nivelador sobre el ácido ya que la fuerza del ácido disuelto no puede exceder a la del disolvente protonado. Por ejemplo, en disolución acuosa, no puede existir ninguna especie ácida que sea un ácido más fuerte que [H3O]+. En disolventes ácidos, como CH3CO2H, H2SO4), se facilita la ionización de las bases; y por consiguiente la mayoría de los ácidos son relativamente débiles en estas condiciones y algunos inclusive se ionizan como bases.
Un disolvente es más probable que promueva la ionización de una molécula ácida disuelta en las siguientes circunstancias.[19]
- Si es un disolvente prótico, capaz de formar enlaces de hidrógeno.
- Si tiene un alto número donador, por lo que es una base de Lewis fuerte.
- Si tiene una alta constante dieléctrica (permitividad relativa), por lo que es un buen disolvente de especies iónicas.
Los valores de pKa de los compuestos orgánicos a menudo se obtienen utilizando disolventes apróticos dimetilsulfóxido (DMSO)[19] y acetonitrilo (ACN).[20]
| Disolvente | Número donador[19] | Constante dieléctrica[19] |
|---|---|---|
| Acetonitrilo | 14 | 37 |
| Dimetilsulfóxido | 30 | 47 |
| Agua | 18 | 78 |
El DMSO se utiliza ampliamente como una alternativa al agua porque tiene una constante dieléctrica menor que el agua, y es menos polar, disolviendo por ello más fácilmente las sustancias hidrofóbicas no polares. Tiene un rango de pKa medible entre 1 y 30. El acetonitrilo es menos básico que el DMSO, y, por ello, en general, los ácidos son más débiles y las bases más fuertes en este disolvente. Algunos valores de pKa a 25 o C para el acetonitrilo (ACN)[21][22][23] y el dimetilsulfóxido (DMSO)[24] se muestran en las siguientes tablas. Los valores para el agua se incluyen a título comparativo.
| HA | ACN | DMSO | agua |
|---|---|---|---|
| ácido p-Toluenosulfónico | 8.5 | 0.9 | fuerte |
| 2,4-Dinitrofenol | 16.66 | 5.1 | 3.9 |
| Ácido Benzoico | 21.51 | 11.1 | 4.2 |
| Ácido Acético | 23.51 | 12.6 | 4.756 |
| Fenol | 29.14 | 18.0 | 9.99 |
| BH+ | |||
| Pirrolidina | 19.56 | 10.8 | 11.4 |
| Trietilamina | 18.82 | 9.0 | 10.72 |
| 1,8-Bis(dimetilamino)naftaleno{{ |11}} | 18.62 | 7.5 | 12.1 |
| Piridina | 12.53 | 3.4 | 5.2 |
| Anilina | 10.62 | 3.6 | 9.4 |
La ionización de los ácidos es menor en un disolvente acídico que en el agua. Por ejemplo, el cloruro de hidrógeno es un ácido débil cuando se disuelve en ácido acético. Esto es debido a que el ácido acético es una base mucho más débil que el agua.
- HCl + CH3CO2H
 Cl− + CH3C(OH)2+
Cl− + CH3C(OH)2+
- ácido + base
 base conjugada + ácido conjugado
base conjugada + ácido conjugado
Compare esta reacción con lo que ocurre cuando el ácido acético se disuelve en el disolvente más acídico ácido sulfúrico puro[25]
- H2SO4 + CH3CO2H
 HSO4− + CH3C(OH)2+
HSO4− + CH3C(OH)2+
La especie poco probable diol geminal diol CH3C(OH)2+ es estable en estos entornos. Para soluciones acuosas la función de acidez más adecuada es la escala de pH.[26] Se han propuesto otras funciones de acidez para medios no acuosos, la más notable es la función de acidez de Hammett, H0, para medios superácidos y su versión modificada H− para medios superbásicos.[27]
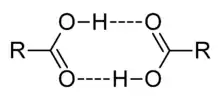
En disolventes apróticos, se pueden formar oligómeros por enlace de hidrógeno, como el conocido dímero del ácido acético. Un ácido también puede formar enlaces de hidrógeno con su base conjugada. Este proceso, conocido como homoconjugación, tiene el efecto de aumentar la acidez de los ácidos, reduciendo sus valores efectivos de pKa, mediante la estabilización de la base conjugada. La homoconjugación aumenta en un factor de casi 800 el poder donador de protones del ácido toluenosulfónico en una solución de acetonitrilo.[28] En soluciones acuosas, la homoconjugation no se produce, porque el agua forma enlaces de hidrógeno más fuertes a la base conjugada que al ácido.
Mezcla de disolventes
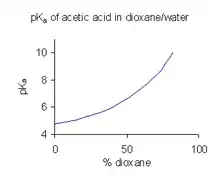
Cuando un compuesto tiene una solubilidad limitada en agua es una práctica corriente (en la industria farmacéutica, por ejemplo) determinar los valores de pKa en una mezcla de disolventes tal como agua/dioxano o agua/metanol, en las que el compuesto es más soluble.[30] En el ejemplo que se muestra a la derecha, el valor de pKa aumenta bruscamente con el porcentaje creciente de dioxano al disminuir la constante dieléctrica de la mezcla.
Un valor de pKa obtenido en una mezcla de disolventes no puede utilizarse directamente para soluciones acuosas. La razón de esto es que cuando el disolvente está en su estado estándar su actividad se “define” como la unidad. Por ejemplo, el estado estándar del agua:dioxano 9:1 es precisamente la mezcla disolvente, sin solutos añadidos. Para obtener el valor de pKa para utilizar en disoluciones acuosas tienen que ser extrapolados a una concentración de codisolvente de cero a partir de los valores obtenidos de varias mezclas de codisolvente.
Estos hechos quedan ocultados por la omisión del disolvente en la expresión que se utiliza normalmente para definir el pKa pero los valores de pKa obtenidos en una determinada mezcla de disolventes dada se puede comparar con cualquier otra, dando las fuerzas ácidas relativas. Lo mismo es cierto para los valores de pKa obtenidos en un disolvente no acuoso particular tal como el DMSO.
Hasta el momento actual, no se ha desarrollado una escala de constantes de disociación universal e independiente del disolvente, ya que no se conoce la forma de comparar los estados estándar de dos disolventes diferentes.
Factores que afectan a los valores de pKa
La segunda regla de Pauling establece que pKa,1 para los ácidos de fórmula XmO(OH)n es aproximadamente independiente de n y X, tal que pKa,1(m = 0) ≈ 8; pKa,1(m = 1) ≈ 2; pKa,1(m = 2) ≈ -3; pKa,1(m = 3) < -10. [13] Esto está relacionado con el estado de oxidación del átomo central X: cuanto mayor sea el estado de oxidación más fuerte es la fuerza del oxoácido. Por ejemplo, el pKa(HClO) = 7,2; pKa(HClO2) = 2,0; pKa(HClO3) = -1 y el HClO4 es un ácido fuerte.

Con los ácidos orgánicos los efectos inductivos y los efecto mesómeros afectan a los valores de pKa. Un ejemplo sencillo es el proporcionado por el efecto de la sustitución de los átomos de hidrógeno en el ácido acético por el átomo más electronegativo de cloro. El efecto de atracción de los electrones de los sustituyentes hace la ionización más fácil, por lo que los sucesivos valores de pKa disminuyen en la serie 4,7, 2,8, 1,3 y 0,7, cuando están presentes 0, 1, 2 o 3 átomos de cloro.[31] La ecuación de Hammett, proporciona una expresión general para el efecto de los sustituyentes.[32]
Ka es la constante de disociación de un compuesto sustituido, K0 es la constante de disociación cuando el sustituyente es hidrógeno, ρ es una propiedad del compuesto sin sustituir y σ tiene un determinado valor para cada sustituyente. Un gráfico de log Ka frente a σ es una línea recta, con ordenada en el origen log K0 y pendiente ρ. Este es un ejemplo de una relación lineal de energía de Gibbs donde el log Ka es proporcional a la variación de energía de Gibbs estándar. Originalmente Hammett[33] formuló la relación con los datos del ácido benzoico con diferentes sustituyentes en posiciones orto- y para-: algunos valores numéricos están en ecuación de Hammett. Este y otros estudios permiten ordenar los sustituyentes de acuerdo con su poder de atracción de electrones o de repulsión de electrones, y distinguir entre los efectos inductivos y mesómeros.[34][35]
Los alcoholes normalmente no se comportan como ácidos en agua, pero la presencia de un doble enlace adyacente al grupo OH puede disminuir considerablemente el pKa por el mecanismo de tautomería ceto-enólica. El ácido ascórbico es un ejemplo de este efecto. La dicetona 2,4-pentanodiona (acetilacetona) es también un ácido débil a causa del equilibrio ceto-enólico. En compuestos aromáticos, tales como el fenol, que tienen un sustituyente OH, la conjugación con el anillo aromático en su conjunto aumenta en gran medida la estabilidad de la forma desprotonada.
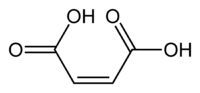
Los efectos estructurales también pueden ser importantes. La diferencia entre ácido fumárico y ácido maleico es un clásico ejemplo. El ácido fumárico es el ácido (E)-1,4-but-2-enodioico, un isómero trans, mientras que el ácido maleico es el correspondiente isómero cis, es decir, el ácido (Z)-1,4-but-2-enodioico (ver isomería cis-trans). El ácido fumárico tiene valores de pKa de aproximadamente 3.5 y 4.5. Por el contrario, el ácido maleico tiene valores de pKa de aproximadamente 1.5 y 6.5. La razón de esta gran diferencia es que cuando se retira un electrón del isómero cis- (ácido maleico) se forma un fuerte enlace de hidrógeno intramolecular con el cercano grupo carboxilo restante. Esto favorece la formación del maleato-H+, y se opone a la eliminación del segundo protón desde esa especie. En el isómero trans, los dos grupos carboxilos están siempre muy alejados, por lo que no se observa el enlace de hidrógeno.[36]
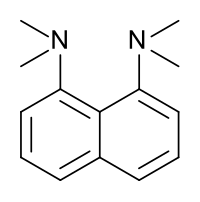
El 1,8-bis(dimetilamino)naftaleno, tiene un valor de pKa de 12,1. Esta es una de las bases de amina más fuerte conocidas. La alta basicidad se atribuye al alivio de la tensión sobre la protonación y los fuertes enlaces de hidrógeno internos.[37][38]
También cabe mencionar en esta sección los efectos del disolvente y de la solvatación. Resulta que, estas influencias son más sutiles que las de un medio dieléctrico como el anteriormente mencionado. Por ejemplo, el orden de basicidad esperado para las metilaminas en fase gaseosa (por los efectos electrónicos de los sustituyentes metilo) y observado:
Me3N > Me2NH > MeNH2 > NH3
es modificado por el agua a:
Me2NH > MeNH2 > Me3N > NH3
Las moléculas de metilamina neutras están enlazadas por puentes de hidrógeno a las moléculas de agua principalmente por interacción a través de un receptor, N-HOH, y solo de vez en cuando con más de un enlace donante, NH-OH 2. Por lo tanto, metilaminas se estabilizan casi en la misma medida por hidratación, independientemente del número de grupos metilo. En marcado contraste, los cationes metilamonio correspondientes siempre utilizar 'todos' los protones disponibles para los donantes NH-OH 2 enlaces. La estabilización relativa de los iones de metilamonio, disminuye por tanto con el número de grupos metilo explicando el orden de basicidad en el agua de las metilaminas.[39]
Termodinámica
Una constante de equilibrio está relacionada con la variación de la energía de Gibbs estándar de la reacción ΔrG°, así para una constante de disociación ácida:
R es la constante de los gases y T es la temperatura absoluta. Experimentalmente se puede considerar que ΔrG°(25 °C) ≈ 5,708 pKa (en kJ mol−1). La energía de Gibbs se compone de un término de entalpía y un término de entropía.[40]
Considerando que la reacción tiene lugar en condiciones isotérmicas, la variación de energía de Gibbs estándar se expresará tal que
La variación de entalpía estándar se puede determinar bien por calorimetría o bien utilizando la ecuación de Van't Hoff, aunque el método calorimétrico es preferible. Cuando la variación de entalpía estándar y la constante de disociación ácida sean medidas, la variación de entropía estándar se calcula fácilmente a partir de la ecuación anterior. En la tabla siguiente, los términos de entropía se han calculado a partir de los valores experimentales de pKa y ΔH°. Los datos fueron cuidadosamente seleccionados y referidos a 25 °C y fuerza iónica nula, en agua.[40]
| Compuesto | Equilibrio | pKa | ΔH° /kJ·mol−1 | −TΔS° /kJ·mol−1 |
|---|---|---|---|---|
| HA = Ácido acético | HA | 4.756 | −0.41 | 27.56 |
| H2A+ = GlicinaH+ | H2A+ | 2.351 | 4.00 | 9.419 |
| HA | 9.78 | 44.20 | 11.6 | |
| H2A = Ácido maleico | H2A | 1.92 | 1.10 | 9.85 |
| HA− | 6.27 | −3.60 | 39.4 | |
| H3A = Ácido cítrico | H3A | 3.128 | 4.07 | 13.78 |
| H2A− | 4.76 | 2.23 | 24.9 | |
| HA2− | 6.40 | −3.38 | 39.9 | |
| HA = Ácido bórico | HA | 9.237 | 13.80 | 38.92 |
| H3A = Ácido fosfórico | H3A | 2.148 | −8.00 | 20.26 |
| H2A− | 7.20 | 3.60 | 37.5 | |
| HA2− | 12.35 | 16.00 | 54.49 | |
| HA− = Hidrógeno sulfato | HA− | 1.99 | −22.40 | 33.74 |
| H2A = Ácido oxálico | H2A | 1.27 | −3.90 | 11.15 |
| HA− | 4.266 | 7.00 | 31.35 |
| Compuesto | Equilibrio | pKa | ΔH° /kJ·mol−1 | −TΔS° /kJ·mol−1 |
|---|---|---|---|---|
| B = Amoníaco | HB+ | 9.245 | 51.95 | 0.8205 |
| B = Metilamina | HB+ | 10.645 | 55.34 | 5.422 |
| B = Trietilamina | HB+ | 10.72 | 43.13 | 18.06 |
El primer punto a destacar es que, cuando pKa > 0, la variación de energía de Gibbs estándar para la reacción de disociación también es positiva; esto es, la disociación de un ácido débil no es un proceso espontáneo. Segundo, algunas reacciones son exotérmicas y otras son endotérmicas, pero, cuando ΔH° < 0, el término −TΔS° es el factor dominante, el cual determina que ΔG° > 0. Finalmente, la contribución de la entropía es siempre desfavorable en estas reacciones.
Téngase en cuenta que la variación de energía estándar de la reacción es para los cambios desde los reactivos en sus estados estándar hasta los productos en sus estados estándar. La variación de energía de Gibbs en el equilibrio es cero, ya que los potenciales químicos de reactivos y productos son iguales en el equilibrio.
Determinación experimental

La determinación experimental de los valores de pKa se realiza normalmente por medio de valoraciones (o titulaciones) en un medio de alta fuerza iónica y a temperatura constante.[41] Un procedimiento típico podría ser como sigue. Una solución del compuesto en el medio se acidifica con un ácido fuerte hasta el punto en que el compuesto está completamente protonado. La solución se valora entonces con una base fuerte hasta que todos los protones han sido arrancados. En cada punto de la valoración se mide el pH utilizando un electrodo de vidrio y un pH-metro. Las constantes de equilibrio se encuentran ajustando los valores calculados de pH a los valores observados, utilizando el método de mínimos cuadrados.[42]
El volumen total de base fuerte añadida debe ser pequeña comparado con el volumen inicial de solución a valorar, a fin de mantener la fuerza iónica aproximadamente constante. Esto asegurará que pKa permanece invariable durante la valoración.
Un curva de valoración calculada para el ácido oxálico se muestra a la derecha. El ácido oxálico tiene valores de pKa de 1,27 and 4,27. Por lo tanto, las regiones de tamponamiento estarán centradas alrededor de pH 1,3 y pH 4,3. Las regiones de tamponamiento llevan la información necesaria para obtener los valores de pKa así cómo la variación de las concentraciones del ácido y su base conjugada en una región tampón.
Entre las dos regiones buffer hay un punto final de la valoración o punto de equivalencia, donde el pH se modifica en alrededor de dos unidades. Este punto final no es claro y es típico de un ácido diprótico cuyas zonas de amortiguamiento se superponen un poco: pKa2 - pKa1 es aproximadamente de tres unidades en este ejemplo. (Si la diferencia en los valores de pK fuera de alrededor de dos o menos, el punto final podría no ser detectable.) El segundo punto final comienza cerca de pH 6,3 y es nítido. Esto indica que todos los protones han sido eliminados. Cuando ocurre esto, la solución no está tamponada y el pH se eleva abruptamente con la adición de una pequeña cantidad de base fuerte. Sin embargo, el pH no seguirá aumentando indefinidamente. Una nueva región de tamponamiento comienza alrededor de pH 11 (pKw - 3), que es donde la autoionización del agua se hace importante.
Es muy difícil medir valores de pH menores de dos en solución acuosa con un electrodo de vidrio, porque la ecuación de Nernst deja de servir a valores tan bajos de pH. Para determinar valores de pK de menos de alrededor de 2 o de más de alrededor de 11valores de menos de aproximadamente 2 o más de alrededor de 11 se pueden utilizar medidas espectrofotométricas[43] o RMN[9][44] en lugar de, o combinadas con, medidas de pH.[45]
Cuando no se puede utilizar el electrodo de vidrio, como en soluciones no acuosas, se utilizan frecuentemente métodos espectrofotométricos.[22] Esto puede incluir medidas de absorbancia o fluorescencia. En ambos casos se supone que la cantidad medida es proporcional a la suma de las contribuciones de cada especie fotoactiva; con las medidas de absorbancia se supone que se aplica la ley de Beer-Lambert.
Las soluciones acuosas con agua normal no se pueden utilizar para medidas de RMN de 1H sino que en su lugar se debe utilizar agua pesada, D2O. Los datos de RMN de 13C, sin embargo, se pueden utilizar con agua normal y los espectros de RMN de 1H se pueden utilizar con medios no acuosos. Las cantidades medidas con RMN son la duración promedio de los desplazamientos químicos, como el intercambio de protones es rápido en la escala de tiempo de RMN, pueden medirse otros desplazamientos químicos, como los de 31P.
Microconstantes

Una base como la espermina tiene unos pocos sitios diferentes donde puede ocurrir la protonación. En este ejemplo, el primer protón puede ir al grupo -NH2 terminal, o a cualquiera de los grupos -NH- internos. Los valores de pKa para la disociación de la espermina protonada en uno u otro de los sitios son ejemplos de microconstantes. No pueden determinarse directamente mediante medidas de pH, absorbancia, fluorescencia o RMN. Sin embargo, el sitio de protonación es muy importante para las funciones biológicas, así se han desarrollado métodos matemáticos para la determinación de microconstantes.[46]
Aplicaciones e importancia
El conocimiento de los valores de pKa es importante para el tratamiento cuantitativo de sistemas que implican equilibrios ácido-base en solución. Existen muchas aplicaciones en bioquímica; por ejemplo, los valores de pKa de las cadenas laterales de las proteínas y aminoácidos son de gran importancia para la actividad de las enzimas y la estabilidad de las proteínas.[47] Los valores de los pKa de las proteínas no siempre pueden medirse directamente, pero pueden calcularse utilizando métodos teóricos. Las soluciones tampón se utilizan ampliamente para proporcionar soluciones en o cerca del pH fisiológico para el estudio de reacciones bioquímicas;[48] el diseño de estas soluciones depende de un conocimiento de los valores de los pKa de sus componentes. Soluciones tampón importantes incluyen el MOPS, que proporciona una solución con pH 7.2, y tricina, que se utiliza en electroforesis en gel.[49][50] El tamponamiento es una parte esencial de la fisiología ácido-base incluyendo la hemostasis ácido-base,[51] y es clave para entender desórdenes tales como el desequilibrio ácido-base.[52][53][54] El punto isoeléctrico de una molécula dad es función de sus valores de pK, así diferentes moléculas tienen puntos isoeléctricos diferentes. Esto permite una técnica llamada Isoelectroenfoque,[55] que se utiliza para la separación de proteínas por Electroforesis en gel bidimensional.
Las soluciones tampón también juegan un papel clave en química analítica. Se utilizan cuando hay una necesidad de fijar el pH de una solución a un valor determinado. En comparación con una solución acuosa, el pH de una solución tampón es relativamente insensible a la adición de una pequeña cantidad de ácido fuerte o de base fuerte. La capacidad de tamponamiento[56] de una solución tampón sencilla es mayor cuando el pH = pKa. En la extracción ácido-base, la eficiencia de la extracción de un compuesto en una fase orgánica, tal como un éter, se puede optimizar ajustando el pH de la fase acuosa utilizando un tampón adecuado. En el pH óptimo, la concentración de las especies eléctricamente neutras se maximiza, una especie así es más soluble en disolventes orgánicos que tienen una constante dieléctrica menor que en el agua. Esta técnica se utiliza para la purificación de ácidos y bases débiles.[57]
A indicador de pH es un ácido o base débil que cambia de color en el rango de transición de pH, que es aproximadamente pKa ± 1. El diseño de un indicador universal requiere de una mezcla de indicadores cuyos valores de pKa adyacentes difieren alrededor de dos unidades, de modo que sus rangos de transición de pH se solapan exactamente.
En farmacología la ionización de un compuesto altera su comportamiento físico y sus propiedades macroscópicas, tales como solubilidad y lipofilicidad (log p). Por ejemplo, la ionización de un compuesto aumentará la solubilidad en agua, pero disminuirá la lipofilicidad. Esto se explota en desarrollo de drogas para aumentar la concentración de un compuesto en la sangre ajustando el pKa de un grupo ionizable.[58]
El conocimiento de los valores de pKa es importante para la comprensión de los complejos de coordinación, que se forman por la interacción de un ion metálico, M+, actuando como un ácido de Lewis, con un ligando, L, actuando como base de Lewis. Sin embargo, el ligando también pueden experimentar reacciones de protonación, por lo que la formación de un complejo en solución acuosa podría representarse simbólicamente por la reacción:
- [M(H2O)n]m+ +LH
 [M(H2O)n−1L](m−1)+ + H3O/sup>C de Pine et al.+
[M(H2O)n−1L](m−1)+ + H3O/sup>C de Pine et al.+
- [M(H2O)n]m+ +LH
Para determinar la constante de equilibrio de esta reacción, en la que el ligando pierde un protón, debe conocerse el pKa de los ligandos protonados. En la práctica, el ligando puede ser poliprótico, por ejemplo el EDTA4- puede aceptar cuatro protones; en cuyo caso, deben conocerse todos los valores de pKa. Además, el ion metálico está sujeta a hidrólisis, es decir, se comporta como un ácido débil, por lo que los valores de pK para las reacciones de hidrólisis también deben ser conocidos.[59] La evaluación de los riesgos asociados con un ácido o una base requieren un conocimiento de los valores de pKa.[60] Por ejemplo, el cianuro de hidrógeno es un gas muy tóxico, porque el ion cianuro inhibe la enzima que contiene hierro citocromo c oxidasa. El cianuro de hidrógeno es un ácido débil en solución acuosa, con un pKa de cerca de 9. En soluciones fuertemente alcalinas, alrededor de pH 11, se deduce que el cianuro de sodio está "totalmente disociado" de modo que el riesgo debido al gas cianuro de hidrógeno es muy reducido. En solución ácida, por el contrario, es muy peligroso porque todo el cianuro está en forma de ácido. La ingestión de cianuro por vía oral, es potencialmente fatal, independiente del pH, debido a la reacción con la citocromo c oxidasa.
En ciencias del medioambiente los equilibrios ácido–base son importantes para los lagos[61] y ríos;[62][63] por ejemplo, los ácidos húmicos son componentes importantes de las aguas naturales. Otro ejemplo ocurre en oceanografía química:[64] en orden a cuantificar la solubilidad del Fe (III) en agua de mar a varias salinidades, se determinaron los valores de pKa para la formación de los productos de hidrólisis del Fe (III), Fe(OH)2+, Fe(OH)2+ y Fe(OH)3, junto con el producto de solubilidad de los hidróxidos de hierro.[65]
Valores para sustancias comunes
Existen múltiples técnicas para determinar el pK, una de una sustancia química, dando lugar a algunas discrepancias entre distintas fuentes. Así los valores medidos varían típicamente en 0,1 unidades de una a otra. . Los datos presentados aquí se refieren a 25 °C, en agua.[3][66] Se pueden encontrar más valores en termodinámica, más arriba.
| Nombre del compuesto químico | Equilibrio | pKa |
|---|---|---|
| B = Adenina | BH22+ |
4.17 |
| BH+ |
9.65 | |
| H3A = Ácido arsénico | H3A |
2.22 |
| H2A− |
6.98 | |
| HA2− |
11.53 | |
| HA = Ácido benzoico | HA |
4.204 |
| HA = Ácido butanoico | HA |
4.82 |
| H2A = Ácido crómico | H2A |
0.98 |
| HA− |
6.5 | |
| B = Codeína | BH+ |
8.17 |
| HA = Cresol | HA |
10.29 |
| HA = Ácido fórmico | HA |
3.751 |
| HA = Ácido fluorhídrico | HA |
3.17 |
| HA = Ácido cianhídrico | HA |
9.21 |
| HA = Seleniuro de hidrógeno | HA |
3.89 |
| HA = Peróxido de hidrógeno (90 %) | HA |
11.7 |
| HA = Ácido láctico | HA |
3.86 |
| HA = Ácido propanoico | HA |
4.87 |
| HA = Fenol | HA |
9.99 |
| H2A = L-(+)-ácido ascórbico | H2A |
4.17 |
| HA− |
11.57 | |
Véase también
- Mecanismo de Grotthuss: sobre cómo se transfieren los protones entre los iones hidronio y las moléculas de agua, lo que da cuenta de la movilidad iónica excepcionalmente alto del protón (animación).
- Acidificación del océano: la disolución del dióxido de carbono atmosférico afecta al pH del agua de mar. La reacción depende del carbono inorgánico total y de los equilibrios de solubilidad de carbonatos sólidos, tales como la caliza y la dolomita.
- Diagrama de predominio: se refiere a los equilibrios en que participan polioxoaniones. Son necesarios los valores de pKa para la construcción de estos diagramas.
- Afinidad de protón: una medida de basicidad en fase gaseosa.
- Constantes de estabilidad de complejos: la formación de un complejo a menudo puede considerarse como una competencia entre los protones y el ion metálico por un ligando, que sea el producto de disociación de un ácido.
- Función de acidez de Hammett: una medida de la acidez que se utiliza para disoluciones de ácidos fuertes muy concentradas, incluyendo los superácidos.
Referencias
- Miessler, G. (1991). Inorganic Chemistry (2nd edición). Prentice Hall. ISBN 0134656598. Capítulo 6: Acid-Base and Donor-Acceptor Chemistry
- Bell, R.P. (1973). The Proton in Chemistry (2ª edición). London: Chapman & Hall. Incluye la discusión de muchos ácidos orgánicos de Brønsted.
- Shriver, D.F; Atkins, P.W. (1999). Inorganic Chemistry (3rd edición). Oxford: Oxford University Press. ISBN 0198503318. Capítulo 5: Acids and Bases
- Housecroft, C.E.; Sharpe, A.G. (2008). Inorganic Chemistry (3rd edición). Prentice Hall. ISBN 0131755536. Capítulo 6: Acids, Bases and Ions in Aqueous Solution
- Headrick, J.M.; Diken, E.G.; Walters, R. S.; Hammer, N. I.; Christie, R.A.; Cui, J.; Myshakin, E.M.; Duncan, M.A.; Johnson, M.A.; Jordan, K.D. (2005). «Spectral Signatures of Hydrated Proton Vibrations in Water Clusters». Science 308: 1765-69. doi:10.1126/science.1113094.
- Smiechowski, M.; Stangret, J. (2006). «Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra». J. Chem. Phys. 125: 204508-204522. doi:10.1063/1.2374891.
- Burgess, J. (1978). Metal Ions in Solution. Ellis Horwood. ISBN 0853120277. Sección 9.1 "Acidity of Solvated Cations" lista muchos valores de pKa.
- Rossotti, F.J.C.; Rossotti, H. (1961). The Determination of Stability Constants. McGraw–Hill. Capítulo 2: Activity and Concentration Quotients
- Popov, K.; Ronkkomaki, H.; Lajunen, L.H.J. (2006). «Guidelines for NMR Measurements for Determination of High and Low pKa Values» (PDF). Pure Appl. Chem. 78 (3): 663-675. doi:10.1351/pac200678030663. Archivado desde el original el 3 de marzo de 2016. Consultado el 10 de agosto de 2011.
- «Project: Ionic Strength Corrections for Stability Constants». International Union of Pure and Applied Chemistry. Archivado desde el original el 29 de octubre de 2008. Consultado el 23 de noviembre de 2008.
- Dasent, W.E. (1982). Inorganic Energetics: An Introduction. Cambridge University Press. ISBN 0521284066. Capítulo 5
- Brown, T.E.; Lemay, H.E.; Bursten,B.E.; Murphy, C.; Woodward, P. (2008). Chemistry: The Central Science (11th edición). New York: Prentice-Hall. p. 689. ISBN 0136006175.
- Greenwood, N.N.; Earnshaw, A. (1997). Chemistry of the Elements (2nd edición). Oxford: Butterworth-Heinemann. p. 50. ISBN 0-7506-3365-4.
- Lide, D.R. (2004). CRC Handbook of Chemistry and Physics, Student Edition (84th edición). CRC Press. ISBN 0849305977. Sección D–152
- Atkins, P.W.; de Paula, J. (2006). Physical Chemistry. Oxford University Press. ISBN 0198700725. Sección 7.4: The Response of Equilibria to Temperature
- Charlot, Gaston (1975). Soluciones acuosas y no acuosas. Toray.
- Baeza Reyes, José Alejandro; García Mendoza, Arturo de Jesús. «Disolventes no acuosos». Consultado el 18/sep/2014.
- Sánchez Batanero, Pedro; Gómez del Río, Ma. Isabel. Química Analítica General. síntesis. p. 324-325. ISBN 84-9756-386-7.
- Plantilla:Loudon p. 317–318
- March, J.; Smith, M. (2007). Advanced Organic Chemistry (6th edición). New York: John Wiley & Sons. ISBN 978-0-471-72091-1. Capítulo 8: Acids and Bases
- Kütt, A.; Movchun, V.; Rodima, T,; Dansauer, T.; Rusanov, E.B.; Leito, I.; Kaljurand, I.; Koppel, J.; Pihl, V.; Koppel, I.; Ovsjannikov, G.; Toom, L.; Mishima, M.; Medebielle, M.; Lork, E.; Röschenthaler, G-V.; Koppel, I.A.; Kolomeitsev, A.A. (2008). «Pentakis(trifluoromethyl)phenyl, a Sterically Crowded and Electron-withdrawing Group: Synthesis and Acidity of Pentakis(trifluoromethyl)benzene, -toluene, -phenol, and -aniline». J. Org. Chem. 73 (7): 2607-2620. doi:10.1021/jo702513w.
- Kütt, A.; Leito, I.; Kaljurand, I.; Sooväli, L.; Vlasov, V.M.; Yagupolskii, L.M.; Koppel, I.A. (2006). «A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile». J. Org. Chem. 71 (7): 2829-2838. doi:10.1021/jo060031y.
- Kaljurand, I.; Kütt, A.; Sooväli, L.; Rodima, T.; Mäemets, V. Leito, I; Koppel, I.A. (2005). «Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales». J. Org. Chem. 70 (3): 1019-1028. doi:10.1021/jo048252w.
- «Bordwell pKa Table (Acidity in DMSO)». Consultado el 2 de noviembre de 2008.
- Housecroft, C.E.; Sharpe, A.G. (2008). Inorganic Chemistry (3rd edición). Prentice Hall. ISBN 0131755536. Capítulo 8: Non-Aqueous Media
- Rochester, C.H. (1970). Acidity Functions. Academic Press. ISBN 0125908504.
- Olah, G.A; Prakash, S; Sommer, J (1985). Superacids. New York: Wiley Interscience. ISBN 0471884693.
- Coetzee, J.F.; Padmanabhan, G.R. (1965). «Proton Acceptor Power and Homoconjugation of Mono- and Diamines». J. Amer. Chem. Soc. 87: 5005-5010. doi:10.1021/ja00950a006.
- Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic chemistry. McGraw–Hill. p. 203. ISBN 0070501157.
- Box, K.J.; Völgyi, G. Ruiz, R. Comer, J.E. Takács-Novák, K., Bosch, E. Ràfols, C. Rosés, M. (2007). «Physicochemical Properties of a New Multicomponent Cosolvent System for the pKa Determination of Poorly Soluble Pharmaceutical Compounds». Helv. Chim. Acta 90 (8): 1538-1553. doi:10.1002/hlca.200790161.
- Pauling, L. (1960). The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry (3rd edición). Ithaca (NY): Cornell University Press. p. 277.
- Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic Chemistry. McGraw–Hill. ISBN 0070501157. Sección 13-3: Quantitative Correlations of Substituent Effects (Part B) – The Hammett Equation
- Hammett, L.P. (1937). «The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives». J. Amer. Chem. Soc. 59 (1): 96-103. doi:10.1021/ja01280a022.
- Hansch, C.; Leo, A.; Taft, R. W. (1991). «A Survey of Hammett Substituent Constants and Resonance and Field Parameters». Chem. Rev. 91 (2): 165-195. doi:10.1021/cr00002a004.
- Shorter, J (1997). Compilation and critical evaluation of structure-reactivity parameters and equations: Part 2. Extension of the Hammett σ scale through data for the ionization of substituted benzoic acids in aqueous solvents at 25 C (Technical Report) 69 (12). pp. 2497-2510. doi:10.1351/pac199769122497.
- Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic chemistry. McGraw–Hill. ISBN 0070501157. Sección 6-2: Structural Effects on Acidity and Basicity
-
Alder, R.W.; Bowman, P.S.; Steele, W.R.S.; Winterman, D.R. (1968). «The Remarkable Basicity of 1,8-bis(dimethylamino)naphthalene». Chem. Commun.: 723
|página=y|páginas=redundantes (ayuda). doi:10.1039/C19680000723. - Alder, R.W. (1989). «Strain Effects on Amine Basicities». Chem. Rev. 89: 1215-1223. doi:10.1021/cr00095a015.
- Fraczkiewicz R (2007). «In Silico Prediction of Ionization». En Testa B and van de Waterbeemd H, ed. Comprehensive medicinal chemistry II, Vol. 5. Amsterdam: Elsevier. pp. 603-626. ISBN 0-08-044518-7.
- Goldberg, R.; Kishore, N.; Lennen, R. (2002). «Thermodynamic Quantities for the Ionization Reactions of Buffers» (PDF, reprinted at NIST). J. Phys. Chem. Ref. Data 31: 231-370. doi:10.1063/1.1416902. Archivado desde el original el 13 de octubre de 2009.
- Martell, A.E.; Motekaitis, R.J. (1992). Determination and Use of Stability Constants. Wiley. ISBN 0471188174. Capítulo 4: Experimental Procedure for Potentiometric pH Measurement of Metal Complex Equilibria
- Leggett, D.J. (1985). Computational Methods for the Determination of Formation Constants. Plenum. ISBN 0306419572.
- Allen, R.I.; Box,K.J.; Comer, J.E.A.; Peake, C.; Tam, K.Y. (1998). «Multiwavelength Spectrophotometric Determination of Acid Dissociation Constants of Ionizable Drugs». J. Pharm. Biomed. Anal. 17 (4–5): 699-641. doi:10.1016/S0731-7085(98)00010-7.
- Szakács, Z.; Hägele, G. (2004). «Accurate Determination of Low pK Values by 1H NMR Titration». Talanta 62: 819-825. doi:10.1016/j.talanta.2003.10.007.
- Box, K.J.; Donkor, R.E. Jupp, P.A. Leader, I.P. Trew, D.F. Turner, C.H. (2008). «The Chemistry of Multi-Protic Drugs Part 1: A Potentiometric, Multi-Vavelength UV and NMR pH Titrimetric Study of the Micro-Speciation of SKI-606». J. Pharm. Biomed. Anal. 47 (2): 303-311. doi:10.1016/j.jpba.2008.01.015.
- Frassineti, C.; Alderighi, L; Gans, P; Sabatini, A; Vacca, A; Ghelli, S. (2003). «Determination of Protonation Constants of Some Fluorinated Polyamines by Means of 13C NMR Data Processed by the New Computer Program HypNMR2000. Protonation Sequence in Polyamines.». Anal. Bioanal. Chem. 376: 1041-1052. doi:10.1007/s00216-003-2020-0.
- Onufriev, A.; Case, D.A; Ullmann G.M. (2001). «A Novel View of pH Titration in Biomolecules». Biochemistry 40: 3413-3419. doi:10.1021/bi002740q.
- Good, N.E.; Winget, G.D.; Winter, W.; Connolly, T.N.; Izawa, S.; Singh, R.M.M. (1966). «Hydrogen Ion Buffers for Biological Research». Biochemistry 5 (2): 467-477. doi:10.1021/bi00866a011.
- Dunn, M.J. (1993). Gel Electrophoresis: Proteins. Bios Scientific Publishers. ISBN 187274821X.
- Martin, R. (1996). Gel Electrophoresis: Nucleic Acids. Bios Scientific Publishers. ISBN 1872748287.
- Brenner, B.M. (Editor); Stein, J.H. (Editor) (1979). Acid–Base and Potassium homeostasis. Churchill Livingstone. ISBN 0443080178.
- Scorpio, R. (2000). Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. Kendall/Hunt Pub. Co. ISBN 0787273740.
- Beynon, R.J.; Easterby, J.S. (1996). Buffer Solutions: The Basics. Oxford: Oxford University Press. ISBN 0199634424.
- Perrin, D.D.; Dempsey, B. (1974). Buffers for pH and Metal Ion Control. London: Chapman & Hall. ISBN 0412117002.
- Garfin, D.(Editor); Ahuja, S. (Editor) (2005). Handbook of Isoelectric Focusing and Proteomics 7. Elsevier. ISBN 0120887525.
- Hulanicki, A. (1987). Reactions of Acids and Bases in Analytical Chemistry. Masson, M.R. (translation editor). Horwood. ISBN 0853123306.
- Eyal, A.M (1997). «Acid Extraction by Acid–Base-Coupled Extractants». Ion Exchange and Solvent Extraction: A Series of Advances 13: 31-94.
- Avdeef, A. (2003). Absorption and Drug Development: Solubility, Permeability, and Charge State. New York: Wiley. ISBN 0471423653.
- Beck, M.T.; Nagypál, I. (1990). Chemistry of Complex Equilibria. Horwood. ISBN 0853121435.
- van Leeuwen, C.J.; Hermens, L. M. (1995). Risk Assessment of Chemicals: An Introduction. Springer. pp. 254–255. ISBN 0792337409.
- Skoog, D.A; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th edición). Thomson Brooks/Cole. ISBN 0-03-035523-0. Capítulo 9-6: Acid Rain and the Buffer Capacity of Lakes
- Stumm, W.; Morgan, J.J. (1996). Water Chemistry. New York: Wiley. ISBN 0471051969.
- Snoeyink, V.L.; Jenkins, D. (1980). Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters. New York: Wiley. ISBN 0471511854.
- Millero, F.J. (2006). Chemical Oceanography (3rd edición). London: Taylor and Francis. ISBN 0849322804.
- Millero, F.J.; Liu, X. (2002). «The Solubility of Iron in Seawater». Marine chemistry 77: 43-54. doi:10.1016/S0304-4203(01)00074-3.
- Speight, J.G. (2005). Lange's Handbook of Chemistry (18th edición). McGraw–Hill. ISBN 0071432205. Capítulo 8
Otras lecturas
- Albert, A.; Serjeant, E.P. (1971). The Determination of Ionization Constants: A Laboratory Manual. Chapman & Hall. ISBN 0412103001. (Edición anterior publicada como Ionization constants of acids and bases. London (UK): Methuen. 1962.)
- Atkins, P.W.; Jones, L. (2008). Chemical Principles: The Quest for Insight (4th edición). W.H. Freeman. ISBN 1-4292-0965-8.
- Housecroft, C.E.; Sharpe, A.G. (2008). Inorganic chemistry (3rd edición). Prentice Hall. ISBN 0131755536. (Disolventes no acuosos)
- Hulanicki, A. (1987). Reactions of Acids and Bases in Analytical Chemistry. Horwood. ISBN 0853123306. (editor de traducción: Mary R. Masson)
- Perrin, D.D.; Dempsey, B.; Serjeant, E.P. (1981). pKa Prediction for Organic Acids and Bases. Chapman & Hall. ISBN 041222190X.
- Reichardt, C. (2003). Solvents and Solvent Effects in Organic Chemistry (3rd edición). Wiley-VCH. ISBN 3-527-30618-8. Capítulo 4: Solvent Effects on the Position of Homogeneous Chemical Equilibria.
- Skoog, D.A.; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th edición). Thomson Brooks/Cole. ISBN 0-03-035523-0.
Enlaces externos
- Extensa bibliografía de valores de pKa en DMSO, acetonitrilo, THF, heptano, 1,2-dicloroetano, y en fase gaseosa.
- All-in-one freeware para cálculos de equilibrio de pH y ácido-base y para la simulación y análisis de curvas de valoración potenciométrica con hojas de cálculo.
- Incluye una base de datos de valores de pKa en fase acuosa, no acuosa y fase gas utilizando SMILES (Simplified molecular input line entry specification) o número de registro CAS.
- Valores de pKa para varios ácidos y bases. Incluye una tabla de productos de solubilidad.
- Free guide to pKa and log p interpretation and measurement Archivado el 10 de agosto de 2016 en Wayback Machine.
- Explanaciones de la relevancia de estas propiedades en farmacología.
- Free online prediction tool (Marvin) pKa, logP, logD etc. From ChemAxon
- Esta obra contiene una traducción derivada de «Acid dissociation constant» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.