Fórmula de rotación de Rodrigues
En la teoría del grupo de rotación SO(3), la fórmula de rotación de Rodrigues, que lleva el nombre de Olinde Rodrigues (1795-1851), es un algoritmo eficiente para rotar un vector en el espacio, dado un eje y un ángulo de rotación. Por extensión, esto se puede usar para transformar los tres vectores de una base para calcular una matriz de rotación en SO(3), el grupo de todas las matrices de rotación, utilizando una notación axial-angular. En otras palabras, la fórmula de Rodrigues proporciona un algoritmo para calcular la aplicación exponencial de so(3) (el álgebra de Lie de SO(3)), sobre SO(3) sin calcular realmente la matriz exponencial completa.
- Este artículo trata sobre la fórmula de rotación de Rodrigues, relacionada con los parámetros de Euler-Rodrigues y con la fórmula de Euler-Rodrigues de una rotación 3D.
Definición
Si v es un vector en ℝ3 y k es un vector unitario que describe un eje de rotación sobre el cual v gira en un ángulo θ según la regla de la mano derecha, la fórmula de Rodrigues para el vector girado vrot es
Una definición alternativa es escribir el vector del eje como un producto vectorial a × b de cualquiera de los dos vectores distintos a cero a y b que definen el plano de rotación, y el sentido del ángulo θ se mide desde a y hacia b. Al dejar que α denote el ángulo entre estos vectores, los dos ángulos θ y α no son necesariamente iguales, pero se miden en el mismo sentido. Entonces el vector del eje unitario se puede escribir
Esta forma puede ser más útil cuando están involucrados dos vectores que definen un plano. Un ejemplo en física es la precesión de Thomas, que incluye la rotación dada por la fórmula de Rodrigues, en términos de dos incrementos de velocidad no colineales, y del eje de rotación que es perpendicular al plano definido por ambas.
Deducción
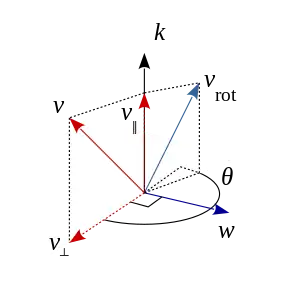

Sea k un vector unitario definiendo un eje de rotación, y sea v un vector para rotar sobre k por el ángulo θ (según la regla de la mano derecha, en sentido contrario a las agujas del reloj en la figura).
Usando el producto escalar y el producto vectorial, el vector v se puede descomponer en componentes paralelos y perpendiculares al eje k,
donde el componente paralelo a k es
llamado vector proyección de v en k, y el componente perpendicular a k es
llamado vector rechazo de v de k.
El vector k × v se puede ver como una copia de v⊥ girada 90° en sentido antihorario alrededor de k, por lo que sus magnitudes son iguales pero las direcciones son perpendiculares. Del mismo modo, el vector k × (k × v) es una copia de v⊥ girada 180° en sentido contrario a las agujas del reloj a través de k, de modo que k × (k × v) y v⊥ son iguales en magnitud pero en direcciones opuestas (es decir, son negativos entre sí, por lo tanto, de signos contrarios). Al expandir el producto mixto se establece la conexión entre los componentes paralelo y perpendicular. La fórmula resultante es a × (b × c) = (a · c)b − (a · b)c dado cualquiera de los tres vectores a, b, c.
La componente paralela al eje no cambiará la magnitud ni la dirección bajo la rotación,
solo la componente perpendicular cambiará de dirección pero conservará su magnitud, de acuerdo con
y como k y v∥ son paralelos, su producto cruzado es cero k × v∥ = 0, por lo que
y se sigue que
Esta rotación es propia, ya que los vectores v⊥ y k × v tienen la misma longitud, y k × v es v⊥ girado 90° en sentido contrario a las agujas del reloj sobre k. Un escalado de v⊥ y k × v utilizando las funciones trigonométricas seno y coseno da el componente perpendicular girado. La forma del componente girado es similar al desarrollo de un vector radial en el plano en coordenadas polares (r, θ) expresado en una base cartesiana 2D
donde ex, ey son vectores unitarios en sus direcciones indicadas.
Ahora el vector rotado completo es
Al sustituir las definiciones de v∥rot y v⊥rot en los resultados de la ecuación en
Notación matricial
Al representar v y k × v como matrices columna, el producto vectorial se puede expresar como una multiplicación de matrices
Haciendo que K denote el "producto vectorial matricial" para el vector unitario k,
La ecuación matricial es, simbólicamente,
para cualquier vector v. (De hecho, K es la matriz única con esta propiedad. Tiene valores propios 0 y ±i).
Iterar el producto cruzado a la derecha equivale a multiplicar por la matriz de productos cruzados a la izquierda, en particular
Además, como k es un vector unitario, K se expresa en función de la unidad de la norma matricial. La fórmula de rotación previa en lenguaje matricial es por lo tanto
Téngase en cuenta que el coeficiente del término principal es ahora 1, en esta notación.
Factorizando v se obtiene la expresión compacta
donde
es la matriz de rotación a través de un ángulo θ en sentido antihorario sobre el eje k, y I es la matriz identidad 3 × 3. Esta matriz R es un elemento del grupo de rotación SO(3) de ℝ3, y K es un elemento del álgebra de Lie que genera ese grupo de Lie (téngase en cuenta que K es asimétrico, lo que caracteriza a ).
En términos de la matriz exponencial,
Para ver que la última identidad se mantiene, se observa que
característica de un grupo uniparamétrico, es decir, exponencial, y que las fórmulas coinciden con θ infinitesimal.
Para una deducción alternativa basada en esta relación exponencial, véase aplicación exponencial de sobre SO(3). Para la asignación inversa, véase aplicación desde SO(3) sobre .
Téngase en cuenta que el dual de Hodge de la rotación es , lo que permite extraer tanto el eje de rotación como el seno del ángulo de rotación de la rotación misma, con la ambigüedad habitual:
donde . La expresión simple anterior resulta del hecho de que el dual de Hodge y es cero, y .
Véase también
Referencias
- Leonhard Euler, "Problema algebraicum ob affectiones prorsus singulares memorabile", 'Commentatio 407 Indicis Enestoemiani, Novi Comm. Acad Sci. Petropolitanae ' '15 (1770), 75–106.
- Olinde Rodrigues, "Des lois géometriques qui regissent les desplacements d 'un systéme solide dans l' space, et the la varia des coordonnées provenant of ces déplacementconsidéééé imépendant des chasquies qui peuvent les produire", J. Mates. Pures Appl. '5' (1840), 380–440.
- Don Koks, (2006) "Exploraciones en física matemática", Springer Science + Business Media, LLC. ISBN 0-387-30943-8. Ch.4, pps 147 y ss. Una ruta indirecta hacia el álgebra geométrica '
Enlaces externos
- Weisstein, Eric W. «Rodrigues' Rotation Formula». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Johan E. Mebius, Derivación de la fórmula de Euler-Rodrigues para rotaciones tridimensionales de la fórmula general para rotaciones de cuatro dimensiones., ArXiv General Mathematics ' '2007.
- Para otro ejemplo descriptivo, consulte http://chrishecker.com/Rigid_Body_Dynamics#Physics_Articles, Chris Hecker, sección de física, parte 4. "La tercera dimensión" - en la página 3, sección "Eje y ángulo", http:// chrishecker.com/images/b/bb/Gdmphys4.pdf