Dinámica de fluidos geofísicos
La dinámica de fluidos geofísicos, en su sentido más amplio, se refiere a la dinámica de fluidos de los flujos naturales, como los flujos de lava, los océanos y las atmósferas planetarias, en la Tierra y otros planetas.[1]
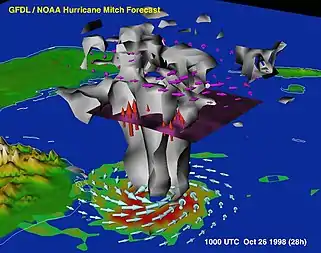
Dos características físicas que son comunes a muchos de los fenómenos estudiados en la dinámica de fluidos geofísicos son la rotación del fluido debido a la rotación planetaria y la estratificación (estratificación). Las aplicaciones de la dinámica de fluidos geofísicos generalmente no incluyen la circulación del manto, que es objeto de geodinámica, o fenómenos de fluidos en la magnetosfera.
Fundamentos
| Geofísica | ||
|---|---|---|
| Subcampos | ||
| Fenómenos físicos | ||
Para describir el flujo de fluidos geofísicos, se necesitan ecuaciones para la conservación del momento (o la segunda ley de Newton) y la conservación de la energía. El primero conduce a las ecuaciones de Navier-Stokes. Generalmente se hacen aproximaciones adicionales. Primero, se supone que el fluido es incompresible. Sorprendentemente, esto funciona bien incluso para un fluido altamente compresible como el aire, siempre y cuando se puedan ignorar las ondas sonoras y de choque.[2] : 2–3 En segundo lugar, se supone que el fluido es un fluido newtoniano, lo que significa que existe una relación lineal entre el esfuerzo cortante τ y la deformación u, por ejemplo
donde μ es la viscosidad.[2] : 2–3 Bajo estos supuestos, las ecuaciones de Navier-Stokes son
El lado izquierdo representa la aceleración que experimentaría una pequeña parcela de fluido en un marco de referencia que se movía con la parcela (un marco de referencia lagrangiano). En un marco de referencia estacionario (euleriano), esta aceleración se divide en la tasa local de cambio de velocidad y advección, una medida de la tasa de flujo dentro o fuera de una pequeña región.[2] : 44–45
La ecuación para la conservación de energía es esencialmente una ecuación para el flujo de calor. Si el calor se transporta por conducción, el flujo de calor se rige por una ecuación de difusión. Si también hay efectos de flotabilidad, por ejemplo, el aumento de aire caliente, puede ocurrir convección natural, también conocida como convección libre.[2] : 171 La convección en el núcleo externo de la Tierra impulsa el geodínamo que es la fuente del campo magnético de la Tierra.[3] En el océano, la convección puede ser térmica (impulsada por el calor), halina (donde la flotabilidad se debe a diferencias en la salinidad) o termohalina, una combinación de los dos.[4]
Flotabilidad y estratificación

El fluido que es menos denso que su entorno tiende a elevarse hasta tener la misma densidad que su entorno. Si no hay mucha entrada de energía al sistema, tenderá a estratificarse. A gran escala, la atmósfera de la Tierra se divide en una serie de capas. Yendo hacia arriba desde el suelo, estos son la troposfera, estratosfera, mesosfera, termosfera y exosfera.[5]
La densidad del aire está determinada principalmente por la temperatura y el contenido de vapor de agua, la densidad del agua de mar por temperatura y salinidad, y la densidad del agua del lago por temperatura. Cuando se produce la estratificación, puede haber capas delgadas en las que la temperatura o alguna otra propiedad cambia más rápidamente con la altura o la profundidad que el fluido circundante. Dependiendo de las principales fuentes de flotabilidad, esta capa puede denominarse picnoclina (densidad), termoclina (temperatura), haloclina (salinidad) o quimiclina (química, incluida la oxigenación).
La misma flotabilidad que da lugar a la estratificación también impulsa las ondas de gravedad. Si las ondas de gravedad ocurren dentro del fluido, se denominan ondas internas.[2] : 208–214
Al modelar flujos impulsados por la flotabilidad, las ecuaciones de Navier-Stokes se modifican utilizando la aproximación de Boussinesq. Esto ignora las variaciones en la densidad, excepto donde se multiplican por la aceleración gravitacional g.[2] : 188
Si la presión depende solo de la densidad y viceversa, la dinámica de los fluidos se llama barotrópica. En la atmósfera, esto corresponde a la falta de frentes, como en los trópicos. Si hay frentes, el flujo es baroclínico y pueden ocurrir inestabilidades como los ciclones.[6]
Rotación
- Efecto Coriolis
- Circulación
- Teorema de circulación de Kelvin
- Ecuación de vorticidad
- Viento termal
- Corriente geostrófica
- Viento geostrófico
- Teorema de Taylor-Proudman
- Equilibrio hidrostático
- Espiral Ekman
- Capa de Ekman
Circulación general
- Circulación atmosférica
- Corriente oceánica
- Dinámica del océano
- Circulación termohalina
- Corriente límite
- Balance de Sverdrup
- Corrientes subsuperficiales
Véase también
- Laboratorio de Dinámica de Fluidos Geofísicos
Referencias
- Vallis, Geoffrey K. (24 de agosto de 2016). «Geophysical fluid dynamics: whence, whither and why?». Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 472 (2192): 20160140. Bibcode:2016RSPSA.47260140V. PMC 5014103. PMID 27616918. doi:10.1098/rspa.2016.0140.
- Tritton, D. J. (1990). Physical Fluid Dynamics (Second edición). Oxford University Press. ISBN 0-19-854489-8.
- Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1996). The magnetic field of the earth: paleomagnetism, the core, and the deep mantle. Academic Press. ISBN 978-0-12-491246-5.
- Soloviev, A.; Klinger, B. (2009). «Open ocean circulation». En Thorpe, ed. Encyclopedia of ocean sciences elements of physical oceanography. London: Academic Press. p. 414. ISBN 9780123757210.
- Zell, Holly (2 de marzo de 2015). «Earth's Upper Atmosphere». NASA (en inglés). Consultado el 20 de febrero de 2017.
- Haby, Jeff. «Barotropic and baroclinic defined». Haby's weather forecasting hints. Consultado el 17 de agosto de 2017.
Otras lecturas
- Cushman-Roisin, Benoit; Beckers, Jean-Marie (October 2011). Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects (Second edición). Academic Press. ISBN 978-0-12-088759-0. Consultado el 14 de octubre de 2010.
- Gill, Adrian E. (1982). Atmosphere : Ocean dynamics. ([Nachdr.] edición). New York: Academic Press. ISBN 978-0122835223.
- McWilliams, James C. (2006). Fundamentals of geophysical fluid dynamics. Cambridge: Cambridge Univ. Press. ISBN 9780521856379.
- Monin, A.S. (1990). Theoretical Geophysical Fluid Dynamics. Dordrecht: Springer Netherlands. ISBN 978-94-009-1880-1.
- Pedlosky, Joseph (2012). Geophysical Fluid Dynamics. Springer Science & Business Media. ISBN 9781468400717.
- Salmon, Rick (1998). Lectures on Geophysical Fluid Dynamics. Oxford University Press. ISBN 9780195355321.
- Vallis, Geoffrey K. (2006). Atmospheric and oceanic fluid dynamics : fundamentals and large-scale circulation (Reprint edición). Cambridge: Cambridge University Press. ISBN 978-0521849692.