Geometría analítica
La geometría analítica es una rama de las matemáticas que estudia las figuras, sus distancias, sus áreas, puntos de intersección, ángulos de inclinación, puntos de división, volúmenes, etcétera. Analiza con detalle los datos de las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Tiene múltiples aplicaciones, más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Las dos cuestiones fundamentales de la geometría analítica son:
- Dado el lugar geométrico de un sistema de coordenadas, para obtener su ecuación.
- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
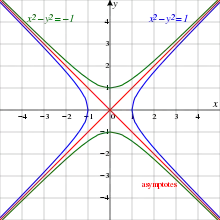
La geometría analítica representa las figuras geométricas mediante la ecuación , donde es una función u otro tipo. Así, las rectas se expresan mediante la ecuación general , las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia, ; la hipérbola, ).
Historia
Antigua Grecia
El matemático griego Menecmo resolvió problemas y demostró teoremas utilizando un método que tenía un gran parecido con el uso de coordenadas y, en ocasiones, se ha sostenido que había introducido la geometría analítica.[1]
Apolonio de Perge, en Sobre la sección determinada, trató los problemas de una manera que puede llamarse geometría analítica de una dimensión; con la cuestión de encontrar puntos en una recta que estuvieran en proporción a los demás.[2] Apolonio en las Cónicas desarrolló además un método que es tan similar a la geometría analítica que a veces se piensa que su trabajo se anticipó al trabajo de Descartes por unos 1800 años. Su aplicación de líneas de referencia, un diámetro y una tangente no es esencialmente diferente de nuestro uso moderno de un marco de coordenadas, donde las distancias medidas a lo largo del diámetro desde el punto de tangencia son las abscisas, y los segmentos paralelos a la tangente e interceptados entre el eje y la curva son las ordenadas. Desarrolló además relaciones entre las abscisas y las ordenadas correspondientes que son equivalentes a ecuaciones retóricas (expresadas en palabras) de curvas. Sin embargo, aunque Apolonio estuvo cerca de desarrollar la geometría analítica, no lo logró ya que no tuvo en cuenta las magnitudes negativas y en todos los casos el sistema de coordenadas se superpuso a una curva dada a posteriori en lugar de a priori. Es decir, las ecuaciones estaban determinadas por curvas, pero las curvas no estaban determinadas por ecuaciones. Las coordenadas, las variables y las ecuaciones eran nociones subsidiarias aplicadas a una situación geométrica específica.[3]
Persia
El matemático persa del siglo XI Omar Jayam vio una fuerte relación entre la geometría y el álgebra y se estaba moviendo en la dirección correcta cuando ayudó a cerrar la brecha entre el álgebra numérica[4] y geométrica con su solución geométrica de las ecuaciones cúbicas generales,[5] pero el paso decisivo vino después con Descartes. A Omar Jayam se le atribuye la identificación de los fundamentos de la geometría algebraica, y su libro Tratado sobre demostraciones de problemas de álgebra (1070), que estableció los principios de la geometría analítica, es parte del cuerpo de matemáticas persas que finalmente se transmitió a Europa.[6] Debido a su enfoque geométrico completo de las ecuaciones algebraicas, Jayampuede considerarse un precursor de Descartes en la invención de la geometría analítica.[7]: 248
Europa Occidental
La geometría analítica fue inventada de forma independiente por René Descartes y Pierre de Fermat,[8][9] aunque a Descartes a veces se le da el crédito exclusivo.[10][11] La geometría cartesiana, el término alternativo utilizado para la geometría analítica, lleva el nombre de Descartes.
Descartes hizo un progreso significativo con los métodos en un ensayo titulado La Géométrie (La Geometría), uno de los tres ensayos adjuntos (apéndices) publicados en 1637 junto con su Discurso sobre el método para dirigir correctamente la razón y buscar la verdad en las ciencias, comúnmente denominado Discurso del método. La Géométrie, escrita en su lengua materna francesa, y sus principios filosóficos, sirvieron de base para el cálculo en Europa. Inicialmente, el trabajo no fue bien recibido debido, en parte, a las muchas lagunas en los argumentos y ecuaciones complicadas. Solo después de la traducción al latín y la adición de comentarios por Frans van Schooten en 1649 (y otros trabajos posteriores) hizo que la obra maestra de Descartes recibiera el debido reconocimiento.[12]
Pierre de Fermat también fue pionero en el desarrollo de la geometría analítica. Aunque no se publicó durante su vida, una forma manuscrita de Ad locos planos et solidos isagoge (Introducción a los lugares planos y sólidos) circulaba en París en 1637, justo antes de la publicación del Discurso de Descartes.[13][14][15] Claramente escrita y bien recibida, la Introducción También sentó las bases para la geometría analítica. La diferencia clave entre los tratamientos de Fermat y Descartes es una cuestión de punto de vista: Fermat siempre comenzaba con una ecuación algebraica y luego describía la curva geométrica que la satisfacía, mientras que Descartes comenzaba con curvas geométricas y producía sus ecuaciones como una de varias propiedades de las curvas.[12] Como consecuencia de este enfoque, Descartes tuvo que lidiar con ecuaciones más complicadas y tuvo que desarrollar los métodos para trabajar con ecuaciones polinómicas de mayor grado. Fue Leonhard Euler quien aplicó por primera vez el método de coordenadas en un estudio sistemático de superficies y curvas espaciales.
Construcciones fundamentales
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados abscisa y ordenada del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la geometría analítica.
Con la geometría analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Este es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Como distancia a los ejes
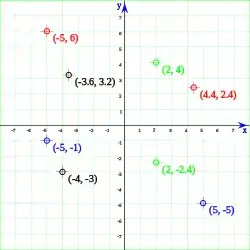
En un plano (v.g. papel milimetrado) se traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado , siendo la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e la distancia al otro eje (al horizontal).
En la coordenada , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
A la coordenada se la suele denominar abscisa del punto, mientras que a la se la denomina ordenada del punto.
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a , así que serán de la forma , mientras que los del eje de ordenadas tendrán abscisa igual a , por lo que serán de la forma .
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia a cada uno de los ejes, luego su abscisa será y su ordenada también será . A este punto —el — se le denomina origen de coordenadas.
Como proyección sobre los ejes
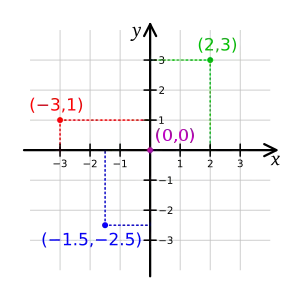
Se consideran dos rectas orientadas, (ejes), perpendiculares entre sí, "x" e "y", con un origen común, el punto O de intersección de ambas rectas.
Teniendo un punto a, al cual se desea determinar las coordenadas, se procede de la siguiente forma:
Por el punto P se trazan rectas perpendiculares a los ejes, éstas determinan en la intersección con los mismos dos puntos, P' (el punto ubicado sobre el eje x) y el punto P'' ( el punto ubicado sobre el eje y).
Dichos puntos son las proyecciones ortogonales sobre los ejes x e y del punto P.
A los Puntos P' y P'' le corresponden por número la distancia desde ellos al origen, teniendo en cuenta que si el punto P' se encuentra a la izquierda de O, dicho número será negativo, y si el punto P'' se encuentra por debajo del punto O, dicho número será negativo.
Los números relacionados con P' y P'', en ese orden son los valores de las coordenadas del punto P.
Ejemplo 1: P' se encuentra a la derecha de O una distancia igual a 2 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 3 unidades. Por lo que las coordenadas de P son (2, 3).
Ejemplo 2: P' se encuentra a la derecha de O una distancia igual a 4 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 5 unidades. Por lo que las coordenadas de P son (4, -5).
Ejemplo 3: P' se encuentra a la izquierda de O una distancia igual a 3 unidades. P'' se encuentra hacia abajo de O, una distancia igual a 2 unidades. Por lo que las coordenadas de P son (-3, -2).
Ejemplo 4: P' se encuentra a la izquierda de O una distancia igual a 6 unidades. P'' se encuentra hacia arriba de O, una distancia igual a 4 unidades. Por lo que las coordenadas de P son (-6, 4).
Ecuaciones de la recta en el plano
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la función lineal de la forma:
Como expresión general, ésta es conocida con el nombre de ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
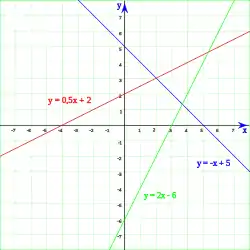
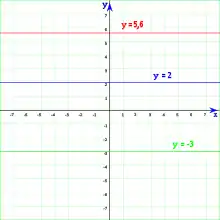
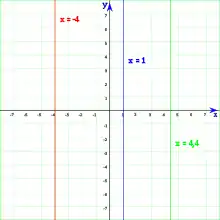
Rectas oblicuas. Rectas horizontales. Rectas verticales.
- Las rectas verticales no cortan al eje de ordenadas y son paralelas a dicho eje y se denominan rectas verticales. El punto de corte con el eje de abscisas es el punto . La ecuación de dichas rectas es:
- Las rectas horizontales no cortan al eje de las abscisas y, por tanto, son paralelas a dicho eje y se denominan rectas horizontales. El punto de corte con el eje de ordenadas es el punto . La ecuación de dichas rectas es:
- Cualquier otro tipo de recta recibe el nombre de recta oblicua. En ellas hay un punto de corte con el eje de abscisas y otro punto de corte con el eje de ordenadas . El valor recibe el nombre de abscisa en el origen, mientras que el se denomina ordenada en el origen.
Secciones cónicas
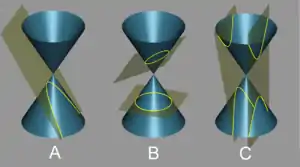
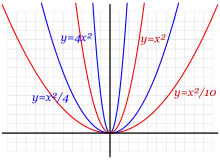

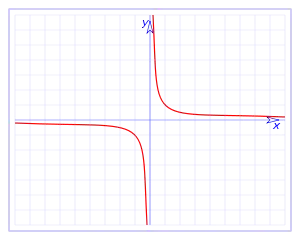
El resultado de la intersección de la superficie de un cono, con un plano, da lugar a lo que se denominan secciones cónicas, que son: la parábola, la elipse (la circunferencia es un caso particular de elipse) y la hipérbola.
- La parábola es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
Una parábola (figura A) cuyo eje de simetría sea paralelo al eje de abcisas se expresa mediante la ecuación:
- La elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
Una elipse (figura B) centrada en los ejes, con longitudes de semieje a y b viene dada por la expresión:
- Si los dos ejes son iguales y los llamamos c:
- el resultado es una circunferencia:
- La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia (resta) de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
La hipérbola (Figura C) tiene por expresión:
Expresión algebraica
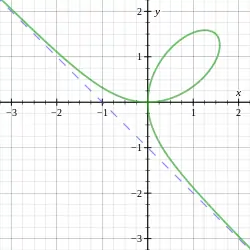
x3 + y3 − 3axy = 0, a = 1.
En coordenadas cartesianas, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:
en la que, en función de los valores de los parámetros, se tendrá:
- h² > ab: hipérbola.
- h² = ab: parábola.
- h² < ab: elipse.
- a = b y h = 0: circunferencia.
Funciones trigonométricas
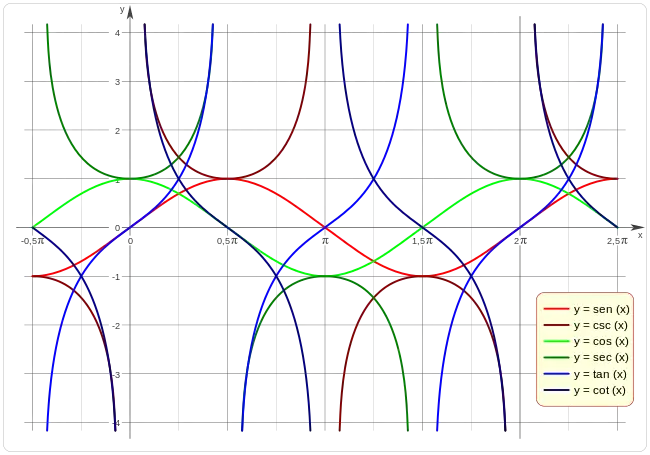
Construcciones en el espacio tridimensional
Los razonamientos sobre la construcción de los ejes coordenados son igualmente válidos para un punto en el espacio y una terna ordenada de números, sin más que introducir una tercera recta perpendicular a los ejes X e Y: el eje Z.
Sin embargo no hay análogo al importantísimo concepto de pendiente de una recta. Una única ecuación lineal del tipo:
Representa en el espacio un plano. Si se pretende representar mediante ecuaciones una recta en el espacio tridimensional necesitaremos especificar, no una, sino dos ecuaciones lineales como las anteriores. De hecho toda recta se puede escribir como intersección de dos planos. Así una recta en el espacio podría quedar representada como:
Es importante notar que la representación anterior no es única, ya que una misma recta puede expresarse como la intersección de diferentes pares de planos. Por ejemplo los dos pares de ecuaciones:
Clasificación de la geometría analítica dentro de la geometría
Desde el punto de vista de la clasificación de Klein de las geometrías (el Programa de Erlangen), la geometría analítica no es una geometría propiamente dicha.
Desde el punto de vista didáctico, la geometría analítica resulta un puente indispensable entre la geometría euclidiana y otras ramas de la matemática y de la propia geometría, como son el propio análisis matemático, el álgebra lineal, la geometría afín, la geometría diferencial o la geometría algebraica.
En física se utiliza los sistemas de coordenadas para la representación de movimientos y vectores entre otras magnitudes.
Historia de la geometría analítica
El nacimiento de la geometría analítica se atribuye a Descartes, por el apéndice La Géométrie incluido en su Discurso del método, publicado en 1637, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Las ideas de Descartes eran algo oscuras y difíciles de entender, y se atribuye su ampliación, desarrollo y divulgación en el mundo matemático a Frans van Schooten y sus colaboradores.[16] Sin embargo, existe una cierta controversia sobre la verdadera paternidad de este método. Omar Khayyam, ya en el siglo XI, utilizó un método muy parecido para determinar ciertas intersecciones entre curvas, aunque es imposible que Fermat y Descartes hayan tenido acceso a su obra.[cita requerida]
El nombre de geometría analítica corrió parejo al de geometría cartesiana, y ambos son indistinguibles. Hoy en día, paradójicamente, se prefiere denominar geometría cartesiana al apéndice del Discurso del método, mientras que se entiende que geometría analítica comprende no solo a la geometría cartesiana (en el sentido mencionado, es decir, al texto apéndice del Discurso del método), sino también todo el desarrollo posterior de la geometría que se base en la construcción de ejes coordenados y la descripción de las figuras mediante funciones —algebraicas o no— hasta la aparición de la geometría diferencial de Gauss (el término "paradójicamente" se debe al hecho de que se usa precisamente el término "geometría cartesiana" para aquello que el propio Descartes bautizó como "geometría analítica"). El problema es que durante ese periodo no había una diferencia clara entre geometría analítica y análisis matemático —esta falta de diferencia se debe precisamente a la identificación hecha en la época entre los conceptos de función y curva—, por lo que resulta a veces muy difícil intentar determinar si el estudio que se está realizando corresponde a una u otra rama.[cita requerida]
La geometría diferencial de curvas sí que permite un estudio mediante un sistema de coordenadas, ya sea en el plano o en el espacio tridimensional. Pero en el estudio de las superficies, en general, aparecen serios obstáculos. Gauss salvó dichos obstáculos creando la geometría diferencial, y marcando con ello el fin de la geometría analítica como disciplina. Con el desarrollo de la geometría algebraica, fue posible certificar totalmente la superación de la geometría analítica.[cita requerida]
La denominación de analítica dada a esta forma de estudiar la geometría provocó que la anterior manera de estudiarla (es decir, la manera axiomático-deductiva, sin la intervención de coordenadas) se terminara denominando, por oposición, geometría sintética, debido a la dualidad análisis-síntesis.[cita requerida]
Notas
- Boyer, Carl B. (1991). «The Age of Plato and Aristotle». A History of Mathematics (Second edición). John Wiley & Sons, Inc. pp. 94–95. ISBN 0-471-54397-7. «Menaechmus apparently derived these properties of the conic sections and others as well. Since this material has a strong resemblance to the use of coordinates, as illustrated above, it has sometimes been maintained that Menaechmus had analytic geometry. Such a judgment is warranted only in part, for certainly Menaechmus was unaware that any equation in two unknown quantities determines a curve. In fact, the general concept of an equation in unknown quantities was alien to Greek thought. It was shortcomings in algebraic notations that, more than anything else, operated against the Greek achievement of a full-fledged coordinate geometry. »
- Boyer, Carl B. (1991). «Apollonius of Perga». A History of Mathematics (Second edición). John Wiley & Sons, Inc. pp. 142. ISBN 0-471-54397-7. «The Apollonian treatise On Determinate Section dealt with what might be called an analytic geometry of one dimension. It considered the following general problem, using the typical Greek algebraic analysis in geometric form: Given four points A, B, C, D on a straight line, determine a fifth point P on it such that the rectangle on AP and CP is in a given ratio to the rectangle on BP and DP. Here, too, the problem reduces easily to the solution of a quadratic; and, as in other cases, Apollonius treated the question exhaustively, including the limits of possibility and the number of solutions. »
- Boyer, Carl B. (1991). «Apollonius of Perga». A History of Mathematics (Second edición). John Wiley & Sons, Inc. pp. 156. ISBN 0-471-54397-7. «The method of Apollonius in the Conics in many respects are so similar to the modern approach that his work sometimes is judged to be an analytic geometry anticipating that of Descartes by 1800 years. The application of references lines in general, and of a diameter and a tangent at its extremity in particular, is, of course, not essentially different from the use of a coordinate frame, whether rectangular or, more generally, oblique. Distances measured along the diameter from the point of tangency are the abscissas, and segments parallel to the tangent and intercepted between the axis and the curve are the ordinates. The Apollonian relationship between these abscissas and the corresponding ordinates are nothing more nor less than rhetorical forms of the equations of the curves. However, Greek geometric algebra did not provide for negative magnitudes; moreover, the coordinate system was in every case superimposed a posteriori upon a given curve in order to study its properties. There appear to be no cases in ancient geometry in which a coordinate frame of reference was laid down a priori for purposes of graphical representation of an equation or relationship, whether symbolically or rhetorically expressed. Of Greek geometry we may say that equations are determined by curves, but not that curves are determined by equations. Coordinates, variables, and equations were subsidiary notions derived from a specific geometric situation; [...] That Apollonius, the greatest geometer of antiquity, failed to develop analytic geometry, was probably the result of a poverty of curves rather than of thought. General methods are not necessary when problems concern always one of a limited number of particular cases. »
- Boyer (1991). «The Arabic Hegemony». A History of Mathematics. pp. 241–242. ISBN 9780471543978. «Omar Khayyam (ca. 1050–1123), the "tent-maker," wrote an Algebra that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the sixteenth century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved." ». Parámetro desconocido
|chapter-url-access=ignorado (ayuda) - Cooper, Glen M. (2003). «Review: Omar Khayyam, the Mathmetician by R. Rashed, B. Vahabzadeh». The Journal of the American Oriental Society 123 (1): 248-249. JSTOR 3217882.
- Mathematical Masterpieces: Further Chronicles by the Explorers, p. 92
- Cooper, G. (2003). Journal of the American Oriental Society,123(1), 248-249.
- Stillwell, John (2004). «Analytic Geometry». Mathematics and its History (Second edición). Springer Science + Business Media Inc. p. 105. ISBN 0-387-95336-1. «the two founders of analytic geometry, Fermat and Descartes, were both strongly influenced by these developments. »
- Boyer, 2004
- Cooke, Roger (1997). «The Calculus». The History of Mathematics: A Brief Course. Wiley-Interscience. pp. 326. ISBN 0-471-18082-3. «The person who is popularly credited with being the discoverer of analytic geometry was the philosopher René Descartes (1596–1650), one of the most influential thinkers of the modern era. »
- Boyer, 2004
- Katz, 1998, pg. 442
- Katz, 1998, pg. 436
- Pierre de Fermat, Varia Opera Mathematica d. Petri de Fermat, Senatoris Tolosani (Toulouse, France: Jean Pech, 1679), "Ad locos planos et solidos isagoge," pp. 91–103.
- "Eloge de Monsieur de Fermat" (Eulogy of Mr. de Fermat), Le Journal des Scavans, 9 February 1665, pp. 69–72. From p. 70: "Une introduction aux lieux, plans & solides; qui est un traité analytique concernant la solution des problemes plans & solides, qui avoit esté veu devant que M. des Cartes eut rien publié sur ce sujet." (An introduction to loci, plane and solid; which is an analytical treatise concerning the solution of plane and solid problems, which was seen before Mr. des Cartes had published anything on this subject.)
- Boyer, 2004, pp. 108-109
Véase también
- Vector
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.
Referencias
Bibliografía
- Colera Jiménez, José (11 de 2007). Matemáticas II, geometría analítica del espacio, Bachillerato. Ejercicio 9 (1 edición). Anaya. p. 48. ISBN 978-84-667-2215-5.
- Colera Jiménez, José (06 de 2002). Matemáticas, geometría analítica plana, 1 Bachillerato. Cuaderno 3 (1 edición). Anaya. p. 56. ISBN 978-84-667-1369-6.
- Alcaide Guindo, Fernando (03 de 2007). Matemáticas, geometría analítica, 4 ESO. Cuaderno de trabajo (1 edición). Ediciones SM. p. 48. ISBN 978-84-675-1508-4.
- Rees, Paul K. (11 de 1972). Geometría analítica (1 edición). Editorial Reverté, S.A. p. 292. ISBN 978-84-291-5110-7.
- Ríos Santos, Agustín (05 de 2004). Geometría analítica (1 edición). Editorial Ecir, S.A. p. 48. ISBN 978-84-7065-858-7.
- Colera Jiménez, José (03 de 2004). Geometria analítica de l'espai, matemàtiques, Batxillerat. Exercicis (en catalán) (1 edición). Editorial Barcanova, S.A. p. 48. ISBN 978-84-489-1559-9.
- Bellón Fernández, Manuel (02 de 2004). Matemáticas, geometría analítica, 4 ESO. Cuaderno 5 (1 edición). Ediciones SM. p. 32. ISBN 978-84-348-8031-3.
- Ruiz Sancho, Jesús María (02 de 2004). Geometría analítica, Bachillerato (1 edición). Anaya. p. 160. ISBN 978-84-667-2612-2.
- González Urbaneja, Pedro Miguel (01 de 2004). Los orígenes de la geometría analítica (1 edición). Fundación Canaria Orotava de Historia de la Ciencia. p. 166. ISBN 978-84-607-9668-8.
- Lehmann, Charles H. Geometría Analítica. ISBN 978-968-18-1176-1.
- Boyer, Carl B. (2004) [1956], History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0.
- Burton, David M. (2011), The History of Mathematics / An Introduction (7th edición), McGraw Hill, ISBN 978-0-07-338315-6.
- Boyer, Carl B. (2004), History of Analytic Geometry, Dover Publications, ISBN 978-0486438320.
- Cajori, Florian (1999), A History of Mathematics, AMS, ISBN 978-0821821022.
- John Casey (1885) Analytic Geometry of the Point, Line, Circle, and Conic Sections, link from Internet Archive.
- Katz, Victor J. (1998), A History of Mathematics: An Introduction (2nd Ed.), Reading: Addison Wesley Longman, ISBN 0-321-01618-1.
- Struik, D. J. (1969), A Source Book in Mathematics, 1200-1800, Harvard University Press, ISBN 978-0674823556.
- Bissell, Christopher C. (1987), «Cartesian geometry: The Dutch contribution», The Mathematical Intelligencer 9 (4): 38-44, doi:10.1007/BF03023730.
- Boyer, Carl B. (1944), «Analytic Geometry: The Discovery of Fermat and Descartes», Mathematics Teacher 37 (3): 99-105, doi:10.5951/MT.37.3.0099.
- Boyer, Carl B. (1965), «Johann Hudde and space coordinates», Mathematics Teacher 58 (1): 33-36, doi:10.5951/MT.58.1.0033.
- Coolidge, J. L. (1948), «The Beginnings of Analytic Geometry in Three Dimensions», American Mathematical Monthly 55 (2): 76-86, JSTOR 2305740, doi:10.2307/2305740.
- Pecl, J., Newton and analytic geometry.