Grafos de Klein
En el campo matemático de teoría de grafos, los grafos de Klein son dos grafos regulares relacionados entre sí, cada uno con 84 aristas. Ambos pueden estar embebidos en superficies orientables de genus 3, en las que forman grafos duales.

El grafo de Klein cúbico
| Grafo de Klein 3-regular | ||
|---|---|---|
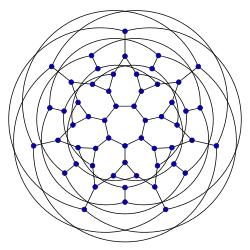 | ||
| Nombre en honor a | Felix Klein | |
| Vértices | 56 | |
| Aristas | 84 | |
| Radio | 6 | |
| Diámetro | 6 | |
| Cintura | 7 | |
| Automorfismos | 336 | |
| Número cromático | 3 | |
| Índice cromático | 3 | |
| Propiedades |
Simétrico Cúbico Hamiltoniano Grafo de Cayley | |
Este es un grafo 3-regular (cúbico) con 56 vértices y 84 aristas, llamado así por el matemático alemán Felix Klein (1849-1925).
Es hamiltoniano, tiene coloración de grafos 3, índice cromático 3, radio 6, diámetro 6 y cintura 7. También es un grafo 3-vértices-conectado y 3-aristas-conectado. Tiene embebido en libro 3 y número de cola 2.[1]
Se puede embeber en una superficie orientable de genus 3 (que se puede representar como una cuártica de Klein), donde forma el mapa de Klein con 24 caras heptagonales, y símbolo de Schläfli {7,3}8.
Según la recopilación de Foster, el grafo de Klein, denominado F056B, es el único grafo simétrico cúbico de 56 vértices que no es bipartito.[2]
Se puede obtener a partir del grafo de Coxeter de 28 vértices.[3]
Propiedades algebraicas
El grupo de automorfismos del grafo de Klein es el grupo PGL2(7) de orden 336, que tiene PSL2(7) como un subgrupo normal. Este grupo actúa transitivamente sobre sus semiaristas, por lo que el grafo de Klein es un grafo simétrico.
El polinomio característico de este grafo de Klein de 56 vértices es igual a:
 Camino hamiltoniano, representado con aristas de tres colores (demostrando que su índice cromático es 3) |
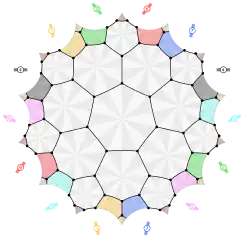 Cuártica de Klein teselada con 24 heptágonos (mapa de Klein) |
El grafo de Klein 7-regular
| Grafo de Klein 7-regular | ||
|---|---|---|
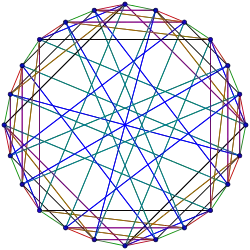 | ||
| Nombre en honor a | Felix Klein | |
| Cintura | 3 | |
| Número cromático | 4 | |
| Índice cromático | 7 | |
| Propiedades |
Simétrico Hamiltoniano | |
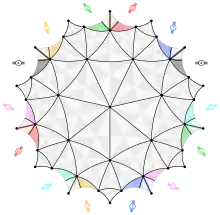
Este es un grafo 7-regular con 24 vértices y 84 aristas, llamado así también por Felix Klein.
Es hamiltoniano, tiene coloración de grafos 4, índice cromático 7, radio 3, diámetro 3 y cintura 3.
Se puede incrustar en una superficie orientable de genus 3, donde forma el dual del mapa de Klein, con 56 caras triangulares, y símbolo de Schläfli {3,7}8.[4]
Es el único grafo de distancia-regular con matriz de intersección , aunque no es un grafo distancia-transitivo.[5]
Propiedades algebraicas
El grupo de automorfismos del grafo de Klein heptavalente es el mismo grupo de orden 336 que el del mapa cúbico de Klein, actuando igualmente transitivamente en sus semiaristas.
El polinomio característico de este grafo de Klein de 24 vértices es igual a:[6]
Referencias
- Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- Conder, M.; Dobcsányi, P. (2002), «Trivalent symmetric graphs up to 768 vertices», J. Combin. Math. Combin. Comput. 40: 41-63..
- Dejter, Italo (2010). From the Coxeter graph to the Klein graph. CiteSeer. arXiv:1002.1960. «citeseerx:10.1.1.188.2580 ».
- Schulte, Egon; Wills, J. M. (1985). «A Polyhedral Realization of Felix Klein's Map {3, 7}8 on a Riemann Surface of Genus 3». J. London Math. Soc. s2-32 (3): 539-547. doi:10.1112/jlms/s2-32.3.539.
- Brouwer, Andries; Cohen, Arjeh; Neumaier, Arnold (1989). Distance-Regular Graphs. Springer Science+Business Media. p. 386. ISBN 978-0-387-50619-7.
- van Dam, E. R.; Haemers, W. H.; Koolen, J. H.; Spence, E. (2006). «Characterizing distance-regularity of graphs by the spectrum». J. Combin. Theory Ser. A 113 (8): 1805-1820. doi:10.1016/j.jcta.2006.03.008.