Gran cuboctaedro truncado

En geometría, el gran cuboctaedro truncado (o cuboctaedro cuasitruncado o cuboctaedro estelatruncado) es un poliedro uniforme no convexo, indexado como U20. Tiene 26 caras, 72 aristas, y 48 vértices.[1] Está representado por el símbolo de Schläfli tr{4/3,3}. A veces se le llama cuboctaedro cuasitruncado porque está relacionado con el cuboctaedro truncado, excepto que las caras octogonales se reemplazan por octagramas {8/3}.

Gran cuboctaedro truncado
Familia: Poliedro estrellado no convexo
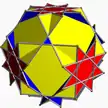Caras 26
Polígonos que forman las caras 12 cuadrados
8 hexágonos regulares
6 octagramas regulares
Aristas 72
Vértices 48
Configuración de vértices 4.6⁄5.8⁄3
Grupo de simetría D5h, [5,2], (*522), orden 20
Poliedro dual Gran disdiaquis dodecaedro
Símbolo de Schläfli t{2,5⁄2} o 5×{}
Símbolo de Wythoff 2 3 4⁄3 |
Símbolo de Coxeter-Dynkin
Propiedades
Poliedro no convexo de vértices uniformes
Modelo 3D de un gran cuboctaedro truncado

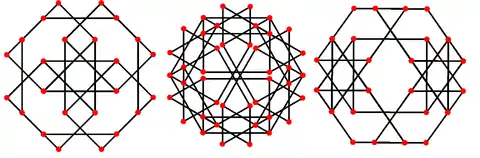
Envolvente convexa

Su envolvente convexa es un cuboctaedro truncado no uniforme. Los esqueletos del cuboctaedro truncado y del gran cuboctaedro truncado forman grafos isomorfos a pesar de su estructura geométrica distinta.


Envolvente convexa
Gran cuboctaedro truncado

Proyecciones ortográficas

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un gran cuboctaedro truncado centrado en el origen son todas las permutaciones de

(±1, ±(1−√2), ±(1−2√2)).

Referencias
  1. Maeder, Roman. «20: great truncated cuboctahedron» [20: gran cuboctaedro truncado]. MathConsult.

Véase también

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.