Gran dirrombicosidodecaedro

Gran dirrombicosidodecaedro
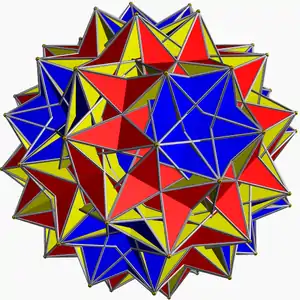	; Modelo 3D
Tipo	poliedro uniforme, poliedro no convexo y poliedro romo
Forma de las caras	triángulo equilátero (40); cuadrado (60); pentagrama (24)
Configuración de vértices	octógono
Dual	gran dirrombicosidodecacrono
Elementos
Vértices	60;
Aristas	240;
Caras	124
Más información
MathWorld	GreatDirhombicosidodecahedron

En geometría, el gran dirrombicosidodecaedro (o gran disicosidisdodecaedro romo) es un poliedro uniforme estrellado, indexado como $U 75$ (la última posición de la lista de Magnus Wenninger). Posee 124 caras (40 triángulos, 60 cuadrados y 24 pentagramas), 240 aristas y 60 vértices.[1]

Este es el único poliedro uniforme no degenerado con más de seis caras que se encuentran en un vértice. En cada vértice coinciden 4 cuadrados que pasan por el eje central del vértice (y por tanto, por el centro de la figura), alternando con dos triángulos y dos pentagramas. Otra característica inusual es que todas las caras aparecen en pares coplanares.

Este es también el único poliedro uniforme que no se puede generar a partir de un triángulo esférico mediante la construcción de Wythoff. Su símbolo de Wythoff, $| 3 ⁄ 2 5 ⁄ 3 3 5 ⁄ 2,$ es una notación especial que lo relaciona con un cuadrilátero esférico. Este símbolo sugiere que es una especie de poliedro romo, excepto que en lugar de que las caras originales estén rodeadas por triángulos como en la mayoría de los poliedros romos, están rodeadas por cuadrados.

Ha sido apodado el monstruo de Miller (en honor a J. C. P. Miller, quien con Harold Scott MacDonald Coxeter y M. S. Longuet-Higgins enumeró los poliedros uniformes en 1954).

Poliedros relacionados

Si la definición de poliedro uniforme se relaja para permitir cualquier número par de caras adyacentes a una arista, entonces esta definición da lugar a otro poliedro: el gran dirrombidodecaedro birromo que tiene los mismos vértices y aristas pero con una disposición diferente de caras triangulares.

Los vértices y aristas también se comparten con los compuestos uniformes de 20 octaedros o de 20 tetrahemihexaedros. De sus 240 aristas, comparte 180 con el gran dodecicosidodecaedro romo.

Envolvente convexa	Gran dodecicosidodecaedro romo	Great Gran dirrombicosidodecaedro
Gran dirrombidodecaedro birromo	Compuesto de veinte octaedros	Compuesto de veinte tetrahemihexaedros

Este poliedro está relacionado con el gran rombicosidodecaedro no convexo (el cuasirrombicosidodecaedro) por un recubrimiento ramificado: existe una correspondencia desde el gran dirrombicosidodecaedro hacia el cuasirrombicosidodecaedro que es 2 a 1 en todas partes, excepto en los vértices.[2]

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un gran dirrombicosidodecaedro son todas las permutaciones pares (con un número par de signos más) de:

\left(0,\pm {\frac {2}{\tau }},\pm {\frac {2}{\sqrt {\tau }}}\right),\left(\pm \left(-1+{\frac {1}{\sqrt {\tau ^{3}}}}\right),\pm \left({\frac {1}{\tau ^{2}}}-{\frac {1}{\sqrt {\tau }}}\right),\pm \left({\frac {1}{\tau }}+{\sqrt {\tau }}\right)\right),

\left(\pm \left({\frac {-1}{\tau }}+{\sqrt {\tau }}\right),\pm \left(-1-{\frac {1}{\sqrt {\tau ^{3}}}}\right),\pm \left({\frac {1}{\tau ^{2}}}+{\frac {1}{\sqrt {\tau }}}\right)\right),

donde τ = (1+√5)/2 es el número áureo (a veces escrito φ). Estos vértices dan como resultado una longitud de borde de 2√2.

Galería

Relleno tradicional	Relleno módulo-2	Vista interior del relleno módulo-2

Referencias

Maeder, Roman. «75: great dirhombicosidodecahedron». MathConsult.
«Great Dirhombicosidodecahedron».

Bibliografía

Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), «Uniform polyhedra», Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246 (916): 401-450, Bibcode:1954RSPTA.246..401C, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183, doi:10.1098/rsta.1954.0003.
Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
Har'El, Z. Solución uniforme para poliedros uniformes, Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El, Kaleido software, Imágenes, imágenes duales
Klitzing, Richard. «3D uniform polyhedra».

Mäder, R. E. Poliedros uniformes. Mathematica J. 3, 48- 57, 1993.

Enlaces externos

Weisstein, Eric W. «Great dirhombicosidodecahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
http://www.mathconsult.ch/showroom/unipoly/75.html
http://www.software3d.com/MillersMonster.php

Datos: Q3101015

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Maeder, Roman. «75: great dirhombicosidodecahedron». MathConsult.

[2] «Great Dirhombicosidodecahedron».