Gran icosaedro
En geometría, el gran icosaedro es uno de los cuatro poliedros de Kepler-Poinsot (poliedros regulares no convexos), con símbolo de Schläfli {3,5/2} y esquema de Coxeter-Dynkin de 
| Gran icosaedro | ||
|---|---|---|
| Familia: Sólido de Kepler-Poinsot | ||
 Imagen del sólido | ||
| Caras | 20 | |
| Aristas | 30 | |
| Vértices | 12 | |
| Grupo de simetría | Icosaédrico (Ih) | |
| Poliedro dual | Gran dodecaedro estrellado | |
Está compuesto de 20 caras triangulares cruzadas, con cinco triángulos que coinciden en cada vértice en una secuencia pentagrámica.
(Véase: Sólido de Kepler-Poinsot)
Imágenes
| Modelo transparente | Densidad | Esquema de Estelación | Desarrollo | Teselado Esférico |
|---|---|---|---|---|
Un modelo transparente del gran icosaedro (Animación)  |
Tiene una densidad de 7, como se muestra en esta sección. |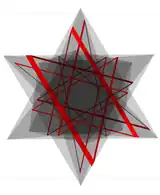
Es un icosaedro estrellado; modelo de Wenninger [W41]; la 16.ª de las 17 estelaciones del icosaedro; y la 7.ª de las 59 estelaciones de Coxeter.  |
 x12(Desarrollo: doce pirámides pentagrámicas isósceles, dispuestas como las caras de un dodecaedro. Cada pliegue de pirámide continuo marca una arista convexa, mientras que las líneas de puntos representan pliegues cóncavos.) |
Este poliedro representa el teselado esférico, con una densidad de 7.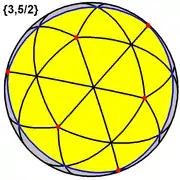
|
Como figura suavizada
El gran icosaedro puede ser construido mediante giros internos uniformes, con caras en diferentes colores y simetría tetraédrica única: 
. Esta construcción se puede denominar como tetraedro retro-suavizado o también como tetratetraedro retro-suavizado. Tiene la simetría del icosaedro presente en el tetraedro suavizado, como faceteado parcial del octaedro truncado (o tetraedro omnitruncado).[1] También puede ser construido con triángulos de 2 colores y simetría piritoédrica 
o como un octaedro retro-suavizado .
| Tetraédrico | Piritoédrico |
|---|---|
 |
 |
|
|
Poliedros relacionados
Comparte la misma disposición de vértices con el icosaedro convexo regular. También comparte la disposición de aristas con el pequeño dodecaedro estrellado.
Una operación de truncamiento, repetidamente aplicada al gran icosaedro, produce una secuencia de poliedros uniformes. Truncando las aristas por debajo de los vértices se produce el gran icosidodecaedro como un gran icosaedro rectificado. El proceso se completa como una doble rectification, reduciendo las caras originales a puntos, y produciendo el gran dodecaedro estrellado.
El gran dodecaedro estrellado truncado es un poliedro degenerado, con 20 caras triangulares de cada uno de sus vértices, y 12 caras pentagonales escondidas ({10/2}) como truncamientos de las caras pentagrámicas originales. La conformación última coincide con dos grandes dodecaedros inscritos en su interior y compartiendo los bordes del icosaedro.
| Nombre | Gran dodecaedro estrellado | Gran dodecaedro estrellado truncado | Gran icosidodecaedro | Gran icosaedro truncado | Gran icosaedro |
|---|---|---|---|---|---|
| Diagrama de Coxeter-Dynkin | |
|
|
|
|
| Imagen |  |
 |
 |
 |
|
Véase también
Referencias
- Richard Klitzing, uniform polyhedra, Great icosahedron
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd edición). Tarquin. ISBN 978-1-899618-32-3. MR 676126. (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104
Enlaces externos
- Eric W. Weisstein, Great icosahedron (Uniform polyhedron) at MathWorld
- Weisstein, Eric W. «Fifteen stellations of the icosahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Uniform polyhedra and duals
| Control de autoridades |
|
|---|
Datos: Q769556
Multimedia: Great icosahedron / Q769556