K-mero

En bioinformática, los k-meros son subcadenas de la longitud contenidas dentro de una secuencia biológica. Principalmente utilizadas en el contexto de genómica computacional y análisis de secuencias, en el cual los k-meros están compuestos de nucleótidos (es decir, A, T, G, y C). Son utilizados para ensamblar secuencias de ADN,[1] mejorar la expresión génica heteróloga[2],[3] identificar especies en muestras metagenómicas,[4] y crear vacunas atenuadas.[5] Normalmente, el término k-mero hace referencia a todas las subsecuencias de longitud de una secuencia, tal que la secuencia AGAT tendría cuatro monómeros (A, G, A y T), tres dímeros (AG, GA, AT), dos trímeros (AGA y GAT) y un tetrámero (AGAT). De manera más general, una secuencia de longitud tendrá k-meros y k-meros posibles en total, es el número de monómeros posibles (p. ej. cuatro en el caso del ADN).

La secuencia ATGG tiene dos k-meros de longitud 3 (trímeros): ATG y TGG.

Introducción

Los k-meros son sencillamente subsecuencias de longitud . Por ejemplo, todos los k-meros posibles de una secuencia de ADN se muestran abajo:

Espectro de los 8-meros para E. coli. Se compara la frecuencia de los 8-meros, octámeros, (es decir, multiplicidades) con su número de ocurrencias.
k-meros para GTAGAGCTGT
k k-meros
1 G, T, A, G, A, G, C, T, G, T
2 GT, TA, AG, GA, AG, GC, CT, TG, GT
3 GTA, TAG, AGA, GAG, AGC, GCT, CTG, TGT
4 GTAG, TAGA, AGAG, GAGC, AGCT, GCTG, CTGT
5 GTAGA, TAGAG, AGAGC, GAGCT, AGCTG, GCTGT
6 GTAGAG, TAGAGC, AGAGCT, GAGCTG, AGCTGT
7 GTAGAGC, TAGAGCT, AGAGCTG, GAGCTGT
8 GTAGAGCT, TAGAGCTG, AGAGCTGT
9 GTAGAGCTG, TAGAGCTGT
10 GTAGAGCTGT

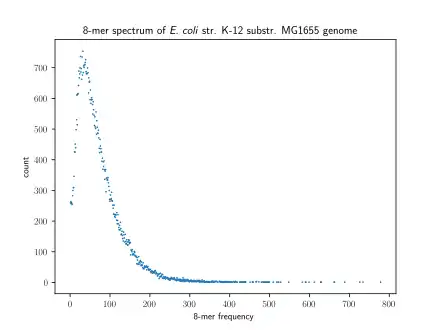
Una forma de visualizar los k-meros es mediante el espectro de k-meros, que muestra la multiplicidad de cada k-mero en una secuencia versus el número de k-meros con aquella multiplicidad.[6] El número de modas (o picos en la distribución) de un espectro de k-meros para el genoma de una especie varía, pero generalmente las especies poseen una distribución unimodal.[7] No obstante, todos los mamíferos tienen una distribución multimodal. Por otro, lado, el número de modas dentro de un espectro de k-meros también puede variar entre regiones de genomas: los humanos poseen espectro de k-meros unimodal en las 5' UTR y en los exones, pero espectro multimodal en las 3' UTR y en los intrones.

Fuerzas que afectan la frecuencia de los k-meros

La frecuencia en el uso del k-mero se ve afectada por numerosas fuerzas, que trabajan en múltiples niveles, a menudo, en conflicto. Los k-meros para valores más altos de k se ven afectados por las fuerzas que también afectan los valores más bajos de k. Por ejemplo, si el 1-mero A no ocurre en una secuencia, tampoco se producirá ninguno de los 2-meros que contienen A (AA, AT, AG y AC).

k = 1

Cuando k = 1, hay cuatro k-meros de ADN, es decir, A, T, G y C. A nivel molecular, hay tres enlaces de hidrógeno entre G y C, mientras que solo hay dos entre A y T. Los enlaces GC, como resultado del enlace de hidrógeno adicional (y de interacciones de apilamiento más fuertes), son más estables térmicamente que los enlaces AT.[8] Los mamíferos y las aves poseen una proporción más alta de G y C con respecto a la de A y T (contenido de GC), de donde surgió la hipótesis de que la estabilidad térmica era un factor determinante de la variación del contenido de GC.[9] No obstante, estudios entre diferentes procariotas no han mostrado evidencia de que el contenido de GC se correlacione con la temperatura, como predeciría la hipótesis de adaptación térmica.[10] De hecho, si la selección natural fuese la fuerza impulsora de la variación del contenido de GC, los cambios de un solo nucleótido, frecuentemente sinónimos, alterarían la aptitud de un organismo.[11]

Antes bien, la evidencia actual sugiere que la conversión génica sesgada por GC (gBGC en inglés) es un factor impulsor de la variación del contenido de GC.[11] La gBGC es un proceso en el cual se reemplaza G y C con A y T durante la recombinación .[12] Este proceso, pese a ser diferente de la selección natural, puede ejercer una presión selectiva sobre el ADN al sesgar hacia los reemplazos por GC que se fijan en el genoma. Como es de esperar, el contenido de GC es mayor en los sitios que experimentan una mayor recombinación.[13] Por otra parte, los organismos con mayores tasas de recombinación presentan un mayor contenido de GC, de acuerdo con los efectos predichos por la hipótesis de la gBGC.[14] En consecuencia, la gBGC puede verse como un «impostor» de la selección natural. Es interesante señalar que la gBGC no parece limitarse a eucariotas,[15] los organimos asexuales como las bacterias y las arqueas también experimentan recombinación por medio de la conversión de genes, un proceso de reemplazo de secuencias homólogas que da como resultado múltiples secuencias idénticas en todo el genoma.[16] Si la recombinación es capaz de aumentar el contenido de GC en todos los dominios de la vida, la gBGC se conserva universalmente. Empero, como los mecanismos exactos y las ventajas o desventajas evolutivas de la gBGC se desconocen actualmente,[17] queda por determinar si la gBGC es un subproducto (mayoritariamente) neutro de la maquinaria molecular de la vida o si está bajo presión de selección natural.

k = 2

A diferencia del contenido de GC, que puede variar considerablemente, los sesgos de dinucleótidos son relativamente constantes en todo el genoma.[18] Si el sesgo de dinucleótidos estuviese sujeto a presiones resultantes de la traducción, entonces habría diferentes patrones de sesgo de dinucleótidos en las regiones codificantes y no codificantes impulsadas por la reducción de la eficiencia de traducción de algunos dinucleótidos.[19] Como no los hay, se puede inferir que las fuerzas que modulan el sesgo de los dinucleótidos son independientes de la traducción. Otra evidencia en contra de las presiones de traducción que afectan el sesgo de dinucleótidos es el hecho de que los sesgos de dinucleótidos de los virus, que dependen en gran medida de la eficiencia de traducción, son moldeados por su familia viral más que por sus anfitriones, de los que secuestran la maquinaria de traducción.[20]

Contrario al creciente contenido de GC de la gBGC existe la supresión de CG, la cual reduce la frecuencia de dímeros CG gracias a la desaminación de dinucleótidos de CG metilados, lo que resulta en sustituciones de CG por TG y en la subsiguiente reducción en el contenido de CG.[21] Esta interacción destaca la interrelación entre las fuerzas que afectan los k-meros para diferentes valores de k.

Un hecho interesante acerca del sesgo hacia dinucléotidos es que este puede servir como medida de «distancia» entre genomas filogenéticamente similares. Los genomas de dos organismos que están estrechamente relacionados comparten más sesgos hacia dinucleótidos que entre dos que están menos relacionados.[18]

k = 3

Hay veinte aminoácidos naturales usados para construir las proteínas que el ADN codifica. No obstante, sólo hay cuatro nucleótidos, de modo que no puede haber una correspondencia unívoca entre nucleótidos y aminoácidos. Asimismo, hay sólo 16 dímeros de ADN, lo que tampoco es suficiente para representar de manera inequívoca cada aminoácido. Aun así, hay 64 trímeros distintos en el ADN, lo que es suficiente para representar inequívocamente cada aminoácido. Estos trímeros se denominan codones. Aunque cada codón sólo se asigna a un aminoácido, cada aminoácido puede estar representado por múltiples codones. Es por esto que la misma secuencia de aminoácidos puede tener múltiples representaciones de ADN. Curiosamente, cada codón de un aminoácido no se usa en proporciones iguales,[22] esto se denomina sesgo en el uso de codones (CUB). Cuando k = 3, se debe hacer una distinción entre la verdadera frecuencia de los trímeros y la del CUB. Por ejemplo, la secuencia ATGGCA tiene cuatro palabras de longitud 3 dentro de ella (ATG, TGG, GGC y GCA), mientras que sólo contiene dos codones (ATG y GCA). Sin embargo, el CUB es un factor importante que impulsa el sesgo hacia el uso de ciertos trímeros (hasta un tercio de este, pues un tercio de los k-meros en una región codificante son codones). Este será el enfoque principal de esta sección.

La causa exacta de la variación entre las frecuencias de los codones no se entiende completamente. Se sabe que la presencia de un codón está relacionada con la abundancia de ARNt, aquellos codones que coinciden con ARNt más abundantes son más frecuentes[22] y las proteínas más altamente expresadas exhiben mayor CUB.[23] Esto sugiere que la selección por eficiencia o precisión traduccional es la fuerza impulsora detrás de la variación en el CUB.

k = 4

Similar al efecto visto en el sesgo hacia dinucleótidos, los sesgos hacia tetranucleótidos de organismos filogenéticamente más relacionados son más parecidos entre sí que entre organismos menos emparentados.[4] Aunque no se conoce bien la causa exacta de la variación en este sesgo, se ha conjeturado que es el resultado del mantenimiento de la estabilidad genética a nivel molecular.[24]

Aplicaciones

La frecuencia de un conjunto de k-meros en el genoma de una especie, en una región genómica, o en una clase de secuencias puede usarse como «firma» de la secuencia subyacente. Comparar estas frecuencias es computacionalmente más fácil que hacer un alineamiento de secuencias y es un método importante en el análisis de secuencias sin alineamientos. También puede ser utilizado como análisis preliminar antes de hacer un alineamiento.

Ensamblaje de secuencias
Esta figura muestra el proceso de dividir las lecturas en k-meros más pequeños (4-meros en este caso) para poder usarlos en un gráfico de De Bruijn. (A) Se muestra el segmento inicial de ADN que se está secuenciando. (B) Se muestra las lecturas realizadas a partir de la secuenciación y cómo estas se alinean. El problema con esta alineación es que se superponen por k - 2, no por k - 1 (que es necesario en los grafos de De Bruijn). (C) Se muestra las lecturas divididas en 4-meros más pequeños. (D) En este punto, se descarta los 4-meros repetidos y luego se muestra la alineación de estos. Estos k-meros se superponen por k - 1 y luego se pueden usar en un gráfico de De Bruijn.

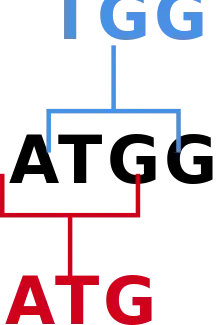
En el ensamblaje de secuencias, los k-meros son utilizados en la construcción de grafos de De Bruijn.[25][26] En un grafo De Bruijn, un k-mero almacenado en un arco de longitud tiene que solaparse con otro k-mero presente en otro arco por para crear un nodo. Las lecturas (reads) generadas a partir de secuenciación de nueva generación usualmente poseen diferentes longitudes de lectura. Por ejemplo, las aquellas provenientes de la secuenciación por tecnología Illumina tienen una longitud de 100. No obstante, el problema con la secuenciación es que sólo se generan fracciones pequeñas de todos los 100-meros (hectómeros) posibles presentes en el genoma. Esto se debe a errores de lectura, pero sobre todo a simples agujeros de cobertura que se producen durante la secuenciación. El problema es que estas fracciones pequeñas de los posibles k-meros violan el supuesto clave de los grafos De Bruijn de que todas las lecturas de k-mero deben solaparse con su k-mero contiguo en el genoma por (lo cual no puede ocurrir si todos los k-meros posibles no están presentes).

La solución a este problema es dividir las lecturas en k-meros más pequeños, de modo que estos representen todos los posibles k-meros de ese tamaño más pequeño presentes en el genoma.[27] Por otro lado, dividir los k-meros en tamaños más pequeños también ayuda a aliviar el inconveniente de tener diferentes longitudes de lectura. En este ejemplo, las cinco lecturas no representan todos los posibles heptámeros del genoma y, como tal, no se puede crear un gráfico de De Bruijn. Empero, cuando se dividen en tetrámeros, las subsecuencias resultantes son suficientes para reconstruir el genoma usando un gráfico de De Bruijn.

Más allá de ser utilizados directamente para ensamblaje de secuencias, los k-meros pueden usarse para detectar el ensamblaje erróneo del genoma al identificar k-meros sobrerrepresentados, lo cual sugiere que secuencias de ADN repetitivo han sido combinadas.[28] Además, los k-meros también se usan para detectar contaminación bacteriana durante el ensamblaje de genoma eucariota, una aproximación tomada del campo de la metagenómica.[29][30]

Elección del tamaño del k-mero

La selección del tamaño del k-mero implica variedad de efectos en el ensamblaje de secuencias. Tales efectos varían bastante entre k-meros de menor y de mayor tamaño; por ello, debe lograrse una comprensión de los distintos tamaños de k-mero para elegir un tamaño adecuado que equilibre los efectos. Los efectos de los tamaños se describen a continuación.

k-meros con tamaños más pequeños
  • Un tamaño de k-mero pequeño disminuirá la cantidad de arcos almacenados en el grafo y, como tal, ayudará a disminuir la cantidad de espacio requerido para almacenar la secuencia de ADN.
  • Tener tamaños más pequeños aumentará la posibilidad de que todos los k-meros se superpongan y tengan las subsecuencias necesarias para construir el grafo de De Bruijn.[31]
  • En cambio, al tener k-meros de menor tamaño, también se corre el riesgo de tener muchos nodos en el grafo que conduce a un solo k-mero. Por lo tanto, esto hará que la reconstrucción del genoma sea más difícil, ya que habría un mayor nivel de ambigüedades al momento de recorrer el grafo debido a la mayor cantidad de nodos que deberán atravesarse.
  • La información se pierde a medida que los k -meros se hacen más pequeños.
    • Por ejemplo: La posibilidad de AGTCGTAGATGCTG es menor que la de ACGT, pero la primera cadena contiene más información (consulte entropía [teoría de la información] para obtener mayor documentación).
  • Los k-meros más cortos también tienen el problema de no poder resolver áreas del ADN donde ocurren microsatélites o regiones repetitivas. Esto se debe a que los k-meros tenderán a sentarse completamente dentro de la región repetitiva y, por lo tanto, es difícil determinar la cantidad de repetición que realmente hay.
    • Por ejemplo: Para la subsecuencia ATGTGTGTGTGTGTACG, la cantidad de repeticiones de TG se perderá si se elige un tamaño de k-mero menor que 16. Esto se debe a que la mayoría de los k-meros se ubicarán en la región repetitiva y posiblemente se descarten como repeticiones del mismo k-mero en lugar de ser identificados como la cantidad de repeticiones.
k-meros con tamaños más grandes
  • Tener k-meros de mayor tamaño aumentará el número de arcos en el grafo, lo que a su vez, aumentará la cantidad de memoria necesaria para almacenar la secuencia de ADN.
  • Al aumentar el tamaño de los k-meros, el número de nodos disminuirá. Esto ayudará con la reconstrucción del genoma, pues habrá menos caminos que recorrer en el grafo.[31]
  • Los k-meros más grandes también corren un mayor riesgo de no poderse solapar con otros k-meros por , de modo que se forman menos nodos. Esto puede provocar desuniones en las lecturas y, como tal, puede dar lugar a una mayor cantidad de cóntigos más cortos.
  • Tamaños más grandes de k-mero ayudan a aliviar el problema de las regiones de repetitivas cortas. Esto se debe al hecho de que el k-mero contendrá un equilibrio entre la región repetitiva y las secuencias de ADN adyacentes (con tal de que sean de un tamaño lo suficientemente grande) que pueden ayudar a resolver la cantidad de repetición en esa región en particular.

Genética y genómica

El sesgo de dinucleótidos se ha aplicado a la detección de islas genéticas asociadas con patogenicidad.[11] Además, existen trabajos donde se ha demostrado que los sesgos por tetranucleótidos son capaces de detectar eficazmente transferencia horizontal de genes tanto en procariotas[32] como en eucariotas.[33]

Otra aplicación de los k-meros está en la taxonomía basada en genómica. Por ejemplo, el contenido de GC se ha utilizado para distinguir entre especies de Erwinia con un éxito moderado.[34] Asimismo, el uso de la Tm, temperatura de fusión del ADN, ha tenido usos taxonómicos. Debido a que los enlaces de GC son más estables térmicamente, las secuencias con un mayor contenido de GC muestran una mayor Tm. En 1987, se propuso el uso de ΔTm como factor para determinar límites entre especies como parte del concepto filogenético de especie, aunque esta propuesta no parece haber ganado terreno dentro de la comunidad científica.[35]

Entre otras aplicaciones de los k-meros dentro de la genética y de la genómica están:

  • Cuantificación de isoformas de ARN a partir de datos de RNA-seq[36]
  • Clasificación de un haplogrupo mitocondrial en humanos[37]
  • Detección de sitios de recombinación en genomas[38]
  • Estimación del tamaño del genoma usando frecuencia de k-meros contra profundidad de k-mero[39][40]
  • Caracterización de islas CpG por regiones flanqueantes[41][42]

Metagenómica

La variación en la frecuencia y espectro de k-mero se usa mucho en metagenómica tanto para análisis[47][48] como para binning (agrupamiento de lecturas o cóntigos y posterior asignación a genomas individuales). En el binning, el desafío es separar las lecturas de secuenciación en «contenedores» (bins en inglés) de lecturas para cada organismo (o unidad taxonómica operativa) para luego ensamblarlas. Por ejemplo, en función de las frecuencias de tetranucleótidos (k = 4), el algoritmo TETRA toma muestras metagenómicas y las agrupa en organismos diferentes.[49] Otras herramientas que también usan la frecuencia de k-mero para el binning metagenómico son CompostBin ( k = 6),[50] PCAHIER,[51] PhyloPythia (5 ≤ k ≤ 6),[52] CLARK ( k ≥ 20),[53] y TACOA (2 ≤ k ≤ 6).[54] En desarrollos recientes también se ha aplicado aprendizaje profundo al binning metagenómico mediante el uso de k-meros.[55]

Otras aplicaciones dentro de la metagenómica incluyen:

  • Recuperación de marcos de lectura a partir de lecturas sin procesar[56]
  • Estimación de la abundancia de especies en muestras metagenómicas[57]
  • Determinación de especies presentes en muestras determinadas[58][59]
  • Identificación de biomarcadores para enfermedades a partir de muestras[60]

Biotecnología

Ciertas aplicaciones biotecnológicas modifican las frecuencias de k-mero en secuencias de ADN para controlar la eficiencia traduccional. En particular, para regular tanto al alza como a la baja las tasas de producción de proteínas.

En la producción de proteínas, se ha utilizado la reducción de la frecuencia de dinucleótidos para obtener tasas más altas de síntesis proteica.[61] Además, el sesgo en el uso de codones puede ser modificado para crear secuencias sinónimas con mayores tasas de expresión proteica.[2][3] Igualmente, la optimización de pares de codones, una combinación de optimización de codones y de dinucleótidos, también se ha empleado con éxito para aumentar la expresión.[62]

La aplicación más estudiada de los k-meros respecto a a disminución en la eficiencia traduccional es la manipulación de pares de codones para atenuar virus con el fin de crear vacunas. Se ha podido recodificar el virus del dengue, causante de la fiebre del dengue, de modo que su sesgo de pares de codones sea más diferente de la preferencia de uso de codones de los mamíferos en comparación con el virus de tipo salvaje.[63] Si bien el virus recodificado contiene una secuencia de aminoácidos idéntica, presenta una patogenicidad significativamente menor pero provoca una respuesta inmunitaria fuerte. Este enfoque también se ha utilizado eficazmente para crear una vacuna contra la influenza,[64] y una vacuna contra el virus del herpes de la enfermedad de Marek (MDV).[5] No obstante, la manipulación del sesgo de pares de codones empleada para atenuar el MDV no reduce eficazmente la oncogenicidad del virus, lo que destaca una debilidad potencial en las aplicaciones biotecnológicas de este enfoque.

Al estudiar los virus y sus hospederos, ha sido posible concluir que el mecanismo molecular que da como resultado la atenuación de los virus es un aumento de dinucleótidos poco adecuados para la traducción.[65][66]

Otra herramienta biotecnológica importante es la predicción de la temperatura de hibridación durante una PCR mediante el análisis del efecto del contenido GC en el punto de fusión del ADN.

Implementación

Seudocódigo

Determinar los posibles k-meros de una lectura se puede hacer simplemente iterando de uno en uno sobre la longitud de la cadena y sacando cada subcadena de longitud . El seudocódigo para lograr lo anterior es el siguiente:

subrutina k-meros(secuencia sec, entero k) es:
  L = longitud(sec)
  arr = nuevo arreglo de L - k + 1 cadena de caracteres vacía

  # itera sobre el número de k-meros en sec, 
  # almacena el n-ésimo k-mero en el arreglo de salida
  para n = 0 a L - k + 1 exclusivo hacer:
    arr[n] = subsecuencia de sec desde inclusive la letra n hasta exclusive la letra n + k 

  devolver arr
Python3
 
def find_kmers(string, k):

      n = len(string)
      kmers = []
    
      for i in range(0, n-k+1):
           kmers.append(string[i:i+k])

      return kmers

En segmentaciones (pipelines) bioinformáticas

Debido a que el número de k-meros crece exponencialmente para valores de k, contar k-meros con valores grandes de k (usualmente > 10) es una tarea computacionalmente difícil. Mientras que implementaciones como el seudocódigo de arriba sirven para trabajar con valores pequeños de k, para aplicaciones de alto rendimiento o cuando k es grande, tales implementaciones deben ser adaptadas. Para solucionar este problema, se han desarrollado varias herramientas:

  • Jellyfish usa una tabla hash sin bloqueo y multiprocesada para el recuento de k-meros y tiene vinculaciones con Python, Ruby y Perl[67]
  • KMC es una herramienta para el recuento de k-meros que utiliza una arquitectura multidisco para optimizar la velocidad[68]
  • Gerbil usa un enfoque de tabla hash pero con soporte adicional para la aceleración de la GPU[69]
  • K-mer Analysis Toolkit (KAT) utiliza una versión modificada de Jellyfish para analizar el recuentos de k-meros[6]

Véase también

Referencias
  1. Compeau, Phillip E C; Pevzner, Pavel A; Tesler, Glenn (November 2011). «How to apply de Bruijn graphs to genome assembly». Nature Biotechnology (en inglés) 29 (11): 987-991. ISSN 1087-0156. PMC 5531759. PMID 22068540. doi:10.1038/nbt.2023.
  2. Welch, Mark; Govindarajan, Sridhar; Ness, Jon E.; Villalobos, Alan; Gurney, Austin; Minshull, Jeremy; Gustafsson, Claes (14 de septiembre de 2009). «Design Parameters to Control Synthetic Gene Expression in Escherichia coli». En Kudla, Grzegorz, ed. PLOS ONE (en inglés) 4 (9): e7002. Bibcode:2009PLoSO...4.7002W. ISSN 1932-6203. PMC 2736378. PMID 19759823. doi:10.1371/journal.pone.0007002.
  3. Gustafsson, Claes; Govindarajan, Sridhar; Minshull, Jeremy (July 2004). «Codon bias and heterologous protein expression». Trends in Biotechnology (en inglés) 22 (7): 346-353. PMID 15245907. doi:10.1016/j.tibtech.2004.04.006.
  4. Perry, Scott C.; Beiko, Robert G. (1 de enero de 2010). «Distinguishing Microbial Genome Fragments Based on Their Composition: Evolutionary and Comparative Genomic Perspectives». Genome Biology and Evolution (en inglés) 2: 117-131. ISSN 1759-6653. PMC 2839357. PMID 20333228. doi:10.1093/gbe/evq004.
  5. Eschke, Kathrin; Trimpert, Jakob; Osterrieder, Nikolaus; Kunec, Dusan (29 de enero de 2018). «Attenuation of a very virulent Marek's disease herpesvirus (MDV) by codon pair bias deoptimization». En Mocarski, Edward, ed. PLOS Pathogens (en inglés) 14 (1): e1006857. ISSN 1553-7374. PMC 5805365. PMID 29377958. doi:10.1371/journal.ppat.1006857.
  6. Mapleson, Daniel; Garcia Accinelli, Gonzalo; Kettleborough, George; Wright, Jonathan; Clavijo, Bernardo J. (22 de octubre de 2016). «KAT: a K-mer analysis toolkit to quality control NGS datasets and genome assemblies». Bioinformatics (en inglés) 33 (4): 574-576. ISSN 1367-4803. PMC 5408915. PMID 27797770. doi:10.1093/bioinformatics/btw663.
  7. Chor, Benny; Horn, David; Goldman, Nick; Levy, Yaron; Massingham, Tim (2009). «Genomic DNA k-mer spectra: models and modalities». Genome Biology (en inglés) 10 (10): R108. ISSN 1465-6906. PMC 2784323. PMID 19814784. doi:10.1186/gb-2009-10-10-r108.
  8. Yakovchuk, P. (30 de enero de 2006). «Base-stacking and base-pairing contributions into thermal stability of the DNA double helix». Nucleic Acids Research (en inglés) 34 (2): 564-574. ISSN 0305-1048. PMC 1360284. PMID 16449200. doi:10.1093/nar/gkj454.
  9. Bernardi, Giorgio (January 2000). «Isochores and the evolutionary genomics of vertebrates». Gene (en inglés) 241 (1): 3-17. PMID 10607893. doi:10.1016/S0378-1119(99)00485-0.
  10. Hurst, Laurence D.; Merchant, Alexa R. (7 de marzo de 2001). «High guanine–cytosine content is not an adaptation to high temperature: a comparative analysis amongst prokaryotes». Proceedings of the Royal Society B: Biological Sciences (en inglés) 268 (1466): 493-497. ISSN 1471-2954. PMC 1088632. PMID 11296861. doi:10.1098/rspb.2000.1397.
  11. Mugal, Carina F.; Weber, Claudia C.; Ellegren, Hans (December 2015). «GC-biased gene conversion links the recombination landscape and demography to genomic base composition: GC-biased gene conversion drives genomic base composition across a wide range of species». BioEssays (en inglés) 37 (12): 1317-1326. PMID 26445215. doi:10.1002/bies.201500058.
  12. Romiguier, Jonathan; Roux, Camille (15 de febrero de 2017). «Analytical Biases Associated with GC-Content in Molecular Evolution». Frontiers in Genetics 8: 16. ISSN 1664-8021. PMC 5309256. PMID 28261263. doi:10.3389/fgene.2017.00016.
  13. Spencer, C.C.A. (1 de agosto de 2006). «Human polymorphism around recombination hotspots: Figure 1». Biochemical Society Transactions (en inglés) 34 (4): 535-536. ISSN 0300-5127. PMID 16856853. doi:10.1042/BST0340535.
  14. Weber, Claudia C; Boussau, Bastien; Romiguier, Jonathan; Jarvis, Erich D; Ellegren, Hans (December 2014). «Evidence for GC-biased gene conversion as a driver of between-lineage differences in avian base composition». Genome Biology (en inglés) 15 (12): 549. ISSN 1474-760X. PMC 4290106. PMID 25496599. doi:10.1186/s13059-014-0549-1.
  15. Lassalle, Florent; Périan, Séverine; Bataillon, Thomas; Nesme, Xavier; Duret, Laurent; Daubin, Vincent (6 de febrero de 2015). «GC-Content Evolution in Bacterial Genomes: The Biased Gene Conversion Hypothesis Expands». En Petrov, Dmitri A., ed. PLOS Genetics (en inglés) 11 (2): e1004941. ISSN 1553-7404. PMC 4450053. PMID 25659072. doi:10.1371/journal.pgen.1004941.
  16. Santoyo, G; Romero, D (April 2005). «Gene conversion and concerted evolution in bacterial genomes». FEMS Microbiology Reviews (en inglés) 29 (2): 169-183. PMID 15808740. doi:10.1016/j.femsre.2004.10.004.
  17. Bhérer, Claude; Auton, Adam (16 de junio de 2014), «Biased Gene Conversion and Its Impact on Genome Evolution», en John Wiley & Sons Ltd, ed., eLS (en inglés) (John Wiley & Sons, Ltd), ISBN 9780470015902, doi:10.1002/9780470015902.a0020834.pub2.
  18. Karlin, Samuel (October 1998). «Global dinucleotide signatures and analysis of genomic heterogeneity». Current Opinion in Microbiology (en inglés) 1 (5): 598-610. PMID 10066522. doi:10.1016/S1369-5274(98)80095-7.
  19. Beutler, E.; Gelbart, T.; Han, J. H.; Koziol, J. A.; Beutler, B. (1 de enero de 1989). «Evolution of the genome and the genetic code: selection at the dinucleotide level by methylation and polyribonucleotide cleavage.». Proceedings of the National Academy of Sciences (en inglés) 86 (1): 192-196. Bibcode:1989PNAS...86..192B. ISSN 0027-8424. PMC 286430. PMID 2463621. doi:10.1073/pnas.86.1.192.
  20. Di Giallonardo, Francesca; Schlub, Timothy E.; Shi, Mang; Holmes, Edward C. (15 de abril de 2017). «Dinucleotide Composition in Animal RNA Viruses Is Shaped More by Virus Family than by Host Species». En Dermody, Terence S., ed. Journal of Virology (en inglés) 91 (8). ISSN 0022-538X. PMC 5375695. PMID 28148785. doi:10.1128/JVI.02381-16.
  21. Żemojtel, Tomasz; kiełbasa, Szymon M.; Arndt, Peter F.; Behrens, Sarah; Bourque, Guillaume; Vingron, Martin (1 de enero de 2011). «CpG Deamination Creates Transcription Factor–Binding Sites with High Efficiency». Genome Biology and Evolution (en inglés) 3: 1304-1311. ISSN 1759-6653. PMC 3228489. PMID 22016335. doi:10.1093/gbe/evr107.
  22. Hershberg, R; Petrov, DA (2008). «Selection on Codon Bias». Annual Review of Genetics 42: 287-299. PMID 18983258. doi:10.1146/annurev.genet.42.110807.091442.
  23. Sharp, Paul M.; Li, Wen-Hsiung (1987). «The codon adaptation index-a measure of directional synonymous codon usage bias, and its potential applications». Nucleic Acids Research (en inglés) 15 (3): 1281-1295. ISSN 0305-1048. PMC 340524. PMID 3547335. doi:10.1093/nar/15.3.1281.
  24. Noble, Peter A.; Citek, Robert W.; Ogunseitan, Oladele A. (April 1998). «Tetranucleotide frequencies in microbial genomes». Electrophoresis 19 (4): 528-535. ISSN 0173-0835. PMID 9588798. doi:10.1002/elps.1150190412.
  25. Nagarajan, Niranjan; Pop, Mihai (2013). «Sequence assembly demystified». Nature Reviews Genetics (en inglés) 14 (3): 157-167. ISSN 1471-0056. PMID 23358380. doi:10.1038/nrg3367.
  26. Li (2010). «De novo assembly of human genomes with massively parallel short read sequencing». Genome Research 20 (2): 265-272. PMC 2813482. PMID 20019144. doi:10.1101/gr.097261.109.
  27. Compeau, P.; Pevzner, P.; Teslar, G. (2011). «How to apply de Bruijn graphs to genome assembly». Nature Biotechnology 29 (11): 987-991. PMC 5531759. PMID 22068540. doi:10.1038/nbt.2023.
  28. Phillippy, Schatz, Pop (2008). «Genome assembly forensics: finding the elusive mis-assembly». Bioinformatics 9 (3): R55. PMC 2397507. PMID 18341692. doi:10.1186/gb-2008-9-3-r55.
  29. Delmont, Eren (2016). «Identifying contamination with advanced visualization and analysis practices: metagenomic approaches for eukaryotic genome assemblies». PeerJ 4: e1839. PMC 4824900. PMID 27069789. doi:10.7717/peerj.1839.
  30. Bemm (2016). «Genome of a tardigrade: Horizontal gene transfer or bacterial contamination?». Proceedings of the National Academy of Sciences 113 (22): E3054-E3056. PMC 4896698. PMID 27173902. doi:10.1073/pnas.1525116113.
  31. Zerbino, Daniel R.; Birney, Ewan (2008). «Velvet: algorithms for de novo short read assembly using de Bruijn graphs». Genome Research 18 (5): 821-829. PMC 2336801. PMID 18349386. doi:10.1101/gr.074492.107.
  32. Goodur, Haswanee D.; Ramtohul, Vyasanand; Baichoo, Shakuntala (11 de noviembre de 2012). «GIDT — A tool for the identification and visualization of genomic islands in prokaryotic organisms». 2012 IEEE 12th International Conference on Bioinformatics & Bioengineering (BIBE): 58-63. ISBN 978-1-4673-4358-9. doi:10.1109/bibe.2012.6399707.
  33. Jaron, K. S.; Moravec, J. C.; Martinkova, N. (15 de abril de 2014). «SigHunt: horizontal gene transfer finder optimized for eukaryotic genomes». Bioinformatics (en inglés) 30 (8): 1081-1086. ISSN 1367-4803. PMID 24371153. doi:10.1093/bioinformatics/btt727.
  34. Starr, M. P.; Mandel, M. (1 de abril de 1969). «DNA Base Composition and Taxonomy of Phytopathogenic and Other Enterobacteria». Journal of General Microbiology (en inglés) 56 (1): 113-123. ISSN 0022-1287. PMID 5787000. doi:10.1099/00221287-56-1-113.
  35. Moore, W. E. C.; Stackebrandt, E.; Kandler, O.; Colwell, R. R.; Krichevsky, M. I.; Truper, H. G.; Murray, R. G. E.; Wayne, L. G. et al. (1 de octubre de 1987). «Report of the Ad Hoc Committee on Reconciliation of Approaches to Bacterial Systematics». International Journal of Systematic and Evolutionary Microbiology (en inglés) 37 (4): 463-464. ISSN 1466-5026. doi:10.1099/00207713-37-4-463.
  36. Patro, Mount, Kingsford (2014). «Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms». Nature Biotechnology 32 (5): 462-464. PMC 4077321. PMID 24752080. arXiv:1308.3700. doi:10.1038/nbt.2862.
  37. Navarro-Gomez (2015). «Phy-Mer: a novel alignment-free and reference-independent mitochondrial haplogroup classifier». Bioinformatics 31 (8): 1310-1312. PMC 4393525. PMID 25505086. doi:10.1093/bioinformatics/btu825.
  38. Wang, Rong; Xu, Yong; Liu, Bin (2016). «Recombination spot identification Based on gapped k-mers». Scientific Reports (en inglés) 6 (1): 23934. Bibcode:2016NatSR...623934W. ISSN 2045-2322. PMC 4814916. PMID 27030570. doi:10.1038/srep23934.
  39. Hozza, Michal; Vinař, Tomáš; Brejová, Broňa (2015), «How Big is that Genome? Estimating Genome Size and Coverage from k-mer Abundance Spectra», en Iliopoulos, Costas; Puglisi, Simon; Yilmaz, eds., String Processing and Information Retrieval (Springer International Publishing) 9309: 199-209, ISBN 9783319238258, doi:10.1007/978-3-319-23826-5_20.
  40. Lamichhaney, Sangeet; Fan, Guangyi; Widemo, Fredrik; Gunnarsson, Ulrika; Thalmann, Doreen Schwochow; Hoeppner, Marc P; Kerje, Susanne; Gustafson, Ulla et al. (2016). «Structural genomic changes underlie alternative reproductive strategies in the ruff (Philomachus pugnax)». Nature Genetics (en inglés) 48 (1): 84-88. ISSN 1061-4036. PMID 26569123. doi:10.1038/ng.3430.
  41. Chae (2013). «Comparative analysis using K-mer and K-flank patterns provides evidence for CpG island sequence evolution in mammalian genomes». Nucleic Acids Research 41 (9): 4783-4791. PMC 3643570. PMID 23519616. doi:10.1093/nar/gkt144.
  42. Mohamed Hashim, Abdullah (2015). «Rare k-mer DNA: Identification of sequence motifs and prediction of CpG island and promoter». Journal of Theoretical Biology 387: 88-100. PMID 26427337. doi:10.1016/j.jtbi.2015.09.014.
  43. Price, Jones, Pevzner (2005). «De novo identification of repeat families in large genomes». Bioinformatics. 21(supp 1): i351-8. PMID 15961478. doi:10.1093/bioinformatics/bti1018.
  44. Meher, Prabina Kumar; Sahu, Tanmaya Kumar; Rao, A.R. (2016). «Identification of species based on DNA barcode using k-mer feature vector and Random forest classifier». Gene (en inglés) 592 (2): 316-324. PMID 27393648. doi:10.1016/j.gene.2016.07.010.
  45. Newburger, Bulyk (2009). «UniPROBE: an online database of protein binding microarray data on protein–DNA interactions». Nucleic Acids Research. 37(supp 1) (Database issue): D77-82. PMC 2686578. PMID 18842628. doi:10.1093/nar/gkn660.
  46. Nordstrom (2013). «Mutation identification by direct comparison of whole-genome sequencing data from mutant and wild-type individuals using k-mers». Nature Biotechnology 31 (4): 325-330. PMID 23475072. doi:10.1038/nbt.2515.
  47. Zhu, Jianfeng; Zheng, Wei-Mou (2014). «Self-organizing approach for meta-genomes». Computational Biology and Chemistry (en inglés) 53: 118-124. PMID 25213854. doi:10.1016/j.compbiolchem.2014.08.016.
  48. Dubinkina; Ischenko; Ulyantsev; Tyakht; Alexeev (2016). «Assessment of k-mer spectrum applicability for metagenomic dissimilarity analysis». BMC Bioinformatics 17: 38. PMC 4715287. PMID 26774270. doi:10.1186/s12859-015-0875-7.
  49. Teeling, H; Waldmann, J; Lombardot, T; Bauer, M; Glöckner, F (2004). «TETRA: a web-service and a stand-alone program for the analysis and comparison of tetranucleotide usage patterns in DNA sequences». BMC Bioinformatics 5: 163. PMC 529438. PMID 15507136. doi:10.1186/1471-2105-5-163.
  50. Chatterji, Sourav; Yamazaki, Ichitaro; Bai, Zhaojun; Eisen, Jonathan A. (2008), «CompostBin: A DNA Composition-Based Algorithm for Binning Environmental Shotgun Reads», en Vingron, Martin; Wong, Limsoon, eds., Research in Computational Molecular Biology (en inglés) (Springer Berlin Heidelberg) 4955: 17-28, ISBN 9783540788386, doi:10.1007/978-3-540-78839-3_3.
  51. Zheng, Hao; Wu, Hongwei (2010). «Short Prokaryotic DNA Fragment Binning Using a Hierarchical Classifier Based on Linear Discriminant Analysis and Principal Component Analysis». Journal of Bioinformatics and Computational Biology (en inglés) 08 (6): 995-1011. ISSN 0219-7200. PMID 21121023. doi:10.1142/S0219720010005051.
  52. McHardy, Alice Carolyn; Martín, Héctor García; Tsirigos, Aristotelis; Hugenholtz, Philip; Rigoutsos, Isidore (2007). «Accurate phylogenetic classification of variable-length DNA fragments». Nature Methods (en inglés) 4 (1): 63-72. ISSN 1548-7091. PMID 17179938. doi:10.1038/nmeth976.
  53. Ounit, Rachid; Wanamaker, Steve; Close, Timothy J; Lonardi, Stefano (2015). «CLARK: fast and accurate classification of metagenomic and genomic sequences using discriminative k-mers». BMC Genomics (en inglés) 16 (1): 236. ISSN 1471-2164. PMC 4428112. PMID 25879410. doi:10.1186/s12864-015-1419-2.
  54. Diaz, Naryttza N; Krause, Lutz; Goesmann, Alexander; Niehaus, Karsten; Nattkemper, Tim W (2009). «TACOA – Taxonomic classification of environmental genomic fragments using a kernelized nearest neighbor approach». BMC Bioinformatics (en inglés) 10 (1): 56. ISSN 1471-2105. PMC 2653487. PMID 19210774. doi:10.1186/1471-2105-10-56.
  55. Fiannaca, Antonino; La Paglia, Laura; La Rosa, Massimo; Lo Bosco, Giosue’; Renda, Giovanni; Rizzo, Riccardo; Gaglio, Salvatore; Urso, Alfonso (2018). «Deep learning models for bacteria taxonomic classification of metagenomic data». BMC Bioinformatics (en inglés) 19 (S7): 198. ISSN 1471-2105. PMC 6069770. PMID 30066629. doi:10.1186/s12859-018-2182-6.
  56. Zhu, Zheng (2014). «Self-organizing approach for meta-genomes». Computational Biology and Chemistry 53: 118-124. PMID 25213854. doi:10.1016/j.compbiolchem.2014.08.016.
  57. Lu, Jennifer; Breitwieser, Florian P.; Thielen, Peter; Salzberg, Steven L. (2 de enero de 2017). «Bracken: estimating species abundance in metagenomics data». PeerJ Computer Science (en inglés) 3: e104. ISSN 2376-5992. doi:10.7717/peerj-cs.104.
  58. Wood, Derrick E; Salzberg, Steven L (2014). «Kraken: ultrafast metagenomic sequence classification using exact alignments». Genome Biology (en inglés) 15 (3): R46. ISSN 1465-6906. PMC 4053813. PMID 24580807. doi:10.1186/gb-2014-15-3-r46.
  59. Rosen, Gail; Garbarine, Elaine; Caseiro, Diamantino; Polikar, Robi; Sokhansanj, Bahrad (2008). «Metagenome Fragment Classification Using -Mer Frequency Profiles». Advances in Bioinformatics (en inglés) 2008: 205969. ISSN 1687-8027. PMC 2777009. PMID 19956701. doi:10.1155/2008/205969.
  60. Wang, Ying; Fu, Lei; Ren, Jie; Yu, Zhaoxia; Chen, Ting; Sun, Fengzhu (3 de mayo de 2018). «Identifying Group-Specific Sequences for Microbial Communities Using Long k-mer Sequence Signatures». Frontiers in Microbiology 9: 872. ISSN 1664-302X. PMC 5943621. PMID 29774017. doi:10.3389/fmicb.2018.00872.
  61. Al-Saif, Maher; Khabar, Khalid SA (2012). «UU/UA Dinucleotide Frequency Reduction in Coding Regions Results in Increased mRNA Stability and Protein Expression». Molecular Therapy (en inglés) 20 (5): 954-959. PMC 3345983. PMID 22434136. doi:10.1038/mt.2012.29.
  62. Trinh, R; Gurbaxani, B; Morrison, SL; Seyfzadeh, M (2004). «Optimization of codon pair use within the (GGGGS)3 linker sequence results in enhanced protein expression». Molecular Immunology 40 (10): 717-722. PMID 14644097. doi:10.1016/j.molimm.2003.08.006.
  63. Shen, Sam H.; Stauft, Charles B.; Gorbatsevych, Oleksandr; Song, Yutong; Ward, Charles B.; Yurovsky, Alisa; Mueller, Steffen; Futcher, Bruce et al. (14 de abril de 2015). «Large-scale recoding of an arbovirus genome to rebalance its insect versus mammalian preference». Proceedings of the National Academy of Sciences (en inglés) 112 (15): 4749-4754. Bibcode:2015PNAS..112.4749S. ISSN 0027-8424. PMC 4403163. PMID 25825721. doi:10.1073/pnas.1502864112.
  64. Kaplan, Bryan S.; Souza, Carine K.; Gauger, Phillip C.; Stauft, Charles B.; Robert Coleman, J.; Mueller, Steffen; Vincent, Amy L. (2018). «Vaccination of pigs with a codon-pair bias de-optimized live attenuated influenza vaccine protects from homologous challenge». Vaccine (en inglés) 36 (8): 1101-1107. PMID 29366707. doi:10.1016/j.vaccine.2018.01.027.
  65. Kunec, Dusan; Osterrieder, Nikolaus (2016). «Codon Pair Bias Is a Direct Consequence of Dinucleotide Bias». Cell Reports (en inglés) 14 (1): 55-67. PMID 26725119. doi:10.1016/j.celrep.2015.12.011.
  66. Tulloch, Fiona; Atkinson, Nicky J; Evans, David J; Ryan, Martin D; Simmonds, Peter (9 de diciembre de 2014). «RNA virus attenuation by codon pair deoptimisation is an artefact of increases in CpG/UpA dinucleotide frequencies». eLife (en inglés) 3: e04531. ISSN 2050-084X. PMC 4383024. PMID 25490153. doi:10.7554/eLife.04531.
  67. Marçais, Guillaume; Kingsford, Carl (15 de marzo de 2011). «A fast, lock-free approach for efficient parallel counting of occurrences of k-mers». Bioinformatics (en inglés) 27 (6): 764-770. ISSN 1460-2059. PMC 3051319. PMID 21217122. doi:10.1093/bioinformatics/btr011.
  68. Deorowicz, Sebastian; Kokot, Marek; Grabowski, Szymon; Debudaj-Grabysz, Agnieszka (15 de mayo de 2015). «KMC 2: fast and resource-frugal k-mer counting». Bioinformatics (en inglés) 31 (10): 1569-1576. ISSN 1460-2059. PMID 25609798. doi:10.1093/bioinformatics/btv022.
  69. Erbert, Marius; Rechner, Steffen; Müller-Hannemann, Matthias (2017). «Gerbil: a fast and memory-efficient k-mer counter with GPU-support». Algorithms for Molecular Biology (en inglés) 12 (1): 9. ISSN 1748-7188. PMC 5374613. PMID 28373894. doi:10.1186/s13015-017-0097-9.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.