Microlente gravitatoria

Microlente se basa en el efecto de lente gravitacional. Un objeto masivo (la lente) doblará la luz de un objeto de fondo brillante (la fuente). Esto puede generar múltiples imágenes distorsionadas, magnificadas e iluminadas de la fuente de fondo.[7]

Es causada por el mismo efecto físico que lentes fuertes y lentes débiles, pero se estudia utilizando técnicas de observación muy diferentes. En lentes fuertes y débiles, la masa de la lente es lo suficientemente grande (masa de una galaxia o un cúmulo de galaxias) que el desplazamiento de la luz por la lente se puede resolver con un telescopio de alta resolución como el Telescopio Espacial Hubble. Con la microlente, la masa de la lente es demasiado baja (masa de un planeta o una estrella) para que el desplazamiento de la luz se observe fácilmente, pero aún se puede detectar el brillo aparente de la fuente. En tal situación, la lente pasará por la fuente en un tiempo razonable, segundos o años en lugar de millones de años. A medida que la alineación cambia, el brillo aparente de la fuente cambia, y esto se puede controlar para detectar y estudiar el evento. Por lo tanto, a diferencia de las lentes gravitacionales fuertes y débiles, un evento de microlente es un fenómeno transitorio desde una perspectiva de escala de tiempo humana.[8]

A diferencia de las lentes fuertes y débiles, ninguna observación puede establecer que se está produciendo microlente. En cambio, el aumento y la disminución del brillo de la fuente deben controlarse a lo largo del tiempo utilizando la fotometría. Esta función de brillo versus tiempo se conoce como curva de luz. Una curva de luz de microlente típica se muestra a continuación:

Typical light curve of gravitational microlensing event (OGLE-2005-BLG-006) with its model fitted (red)

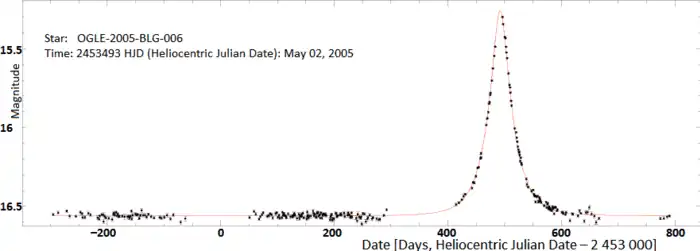
Un evento de microlente típico como este tiene una forma muy simple, y solo se puede extraer un parámetro físico: la escala de tiempo, que está relacionada con la masa del objetivo, la distancia y la velocidad. Sin embargo, hay varios efectos que contribuyen a la forma de eventos de lentes más atípicos:

• Distribución de masa del objetivo: Si la masa de la lente no está concentrada en un solo punto, la curva de luz puede ser dramáticamente diferente, particularmente con los eventos de cruce cáustico, que pueden exhibir fuertes picos en la curva de luz. En la microlente, esto se puede ver cuando la lente es una estrella binaria o un sistema planetario.
• Tamaño de fuente finito: En eventos de microlente extremadamente brillantes o que cambian rápidamente, como los eventos de cruce cáustico, la estrella fuente no puede tratarse como un punto de luz infinitesimalmente pequeño: el tamaño del disco de la estrella e incluso el oscurecimiento de las extremidades puede modificar características extremas.
• Paralaje: Para eventos que duran meses, el movimiento de la Tierra alrededor del Sol puede causar que la alineación cambie ligeramente, afectando la curva de luz.

La mayor parte del enfoque se centra actualmente en los eventos de microlente más inusuales, especialmente aquellos que podrían conducir al descubrimiento de planetas extrasolares. Aunque aún no se ha observado, otra forma de obtener más información de los eventos de microlentes que pronto pueden ser factibles es medir los cambios astrométricos en la posición de la fuente durante el curso del evento[9] e incluso resolver las imágenes separadas con interferometría.[10]

El objeto que causa la microlente en NGC 6553 inclinó la luz de una estrella gigante roja en el fondo.[11][12][13]

En la práctica, debido a que la alineación necesaria es tan precisa y difícil de predecir, la microlentea es muy rara. Los eventos, por lo tanto, generalmente se encuentran con encuestas, que monitorean fotométricamente decenas de millones de estrellas fuente potenciales, cada pocos días durante varios años. Los campos de fondo denso adecuados para tales estudios son las galaxias cercanas, como las Nubes de Magallanes y la galaxia de Andrómeda, y la Vía Láctea. En cada caso, la población de lentes estudiada comprende los objetos entre la Tierra y el campo de origen: para el bulbo, la población de lentes son las estrellas de disco de la Vía Láctea y para las galaxias externas la población de lentes es el halo de la Vía Láctea, así como los objetos en la otra galaxia en sí. La densidad, masa y ubicación de los objetos en estas poblaciones de lentes determina la frecuencia de microlentes a lo largo de esa línea de visión, que se caracteriza por un valor conocido como profundidad óptica debido a la microlente. (Esto no debe confundirse con el significado más común de la profundidad óptica, aunque comparte algunas propiedades.) La profundidad óptica es, en términos generales, la fracción promedio de las estrellas fuente sometidas a microlente en un momento dado, o equivalente a la probabilidad de que un la estrella fuente dada se somete a lentes en un momento dado. El proyecto MACHO encontró que la profundidad óptica hacia el LMC era 1,2×10^-7,[14] y la profundidad óptica hacia la protuberancia es 2,43×10^-6 o aproximadamente 1 en 400.000.[15]

Para complicar la búsqueda está el hecho de que por cada estrella sometida a microlente, hay miles de estrellas que cambian de brillo por otras razones (alrededor del 2% de las estrellas en un campo fuente típico son estrellas naturalmente variables) y otros eventos transitorios (como novas y supernovas), y estos deben eliminarse para encontrar verdaderos eventos de microlente. Después de que se identifica un evento de microlente en progreso, el programa de monitoreo que lo detecta a menudo alerta a la comunidad sobre su descubrimiento, de modo que otros programas especializados puedan seguir el evento más intensamente, con la esperanza de encontrar desviaciones interesantes de la curva de luz típica. Esto se debe a que estas desviaciones, particularmente las debidas a exoplanetas, requieren que se identifique el monitoreo por hora, que los programas de la encuesta no pueden proporcionar mientras se siguen buscando nuevos eventos. La cuestión de cómo priorizar los eventos en progreso para un seguimiento detallado con recursos limitados de observación es muy importante para los investigadores de microlentes de hoy.

En 1704, Isaac Newton sugirió que un rayo de luz podría ser desviado por la gravedad. En 1801, Johann Georg von Soldner calculó la cantidad de deflexión de un rayo de luz de una estrella bajo la gravedad newtoniana. En 1915, Einstein predijo correctamente la cantidad de deflexión bajo la relatividad general, que era el doble de la cantidad pronosticada por von Soldner. La predicción de Einstein fue validada por una expedición de 1919 dirigida por Arthur Eddington, que fue un gran éxito temprano para la relatividad general.[16] En 1924, Orest Chwolson descubrió que las lentes podían producir imágenes múltiples de la estrella. Una predicción correcta de la iluminación concomitante de la fuente, la base de la microlente, fue publicada en 1936 por Einstein.[17] Debido a la improbable alineación requerida, concluyó que "no hay grandes posibilidades de observar este fenómeno". El marco teórico moderno de las lentes gravitacionales se estableció con obras de Yu Klimov (1963), Sidney Liebes (1964) y Sjur Refsdal (1964).[1]

La lente gravitacional se observó por primera vez en 1979, en la forma de un cuásar con lente de una galaxia en primer plano. Ese mismo año, Kyongae Chang y Sjur Refsdal mostraron que las estrellas individuales en la galaxia de la lente podían actuar como lentes más pequeñas dentro de la lente principal, lo que causaba fluctuaciones en las imágenes del cuásar en una escala de meses, también conocida como lente Chang-Refsdal.[18] Bohdan Paczyński utilizó por primera vez el término "microlente" para describir este fenómeno. Este tipo de microlente es difícil de identificar debido a la variabilidad intrínseca de los cuásares.

En 1986, Paczyński propuso usar microlentes para buscar materia oscura en forma de objeto masivo de halo compacto (MACHO) en el halo galáctico, mediante la observación de estrellas de fondo en una galaxia cercana. Dos grupos de físicos de partículas que trabajan en materia oscura escucharon sus charlas y se unieron a los astrónomos para formar la colaboración anglo-australiana MACHO[19] y la francesa EROS.[20]

En 1986, Robert J. Nemiroff predijo la probabilidad de microlente[21] y calculó las curvas de luz inducidas por microlentes básicas para varias configuraciones posibles de lente-fuente en su tesis de 1987.[22]

En 1991, Mao y Paczyński sugirieron que la microlentencia podría usarse para encontrar compañeros binarios para las estrellas, y en 1992 Gould y Loeb demostraron que la microlentencia puede usarse para detectar exoplanetas. En 1992, Paczyński fundó el experimento de microlente OGLE,[23] que comenzó a buscar eventos en la dirección del Centro galáctico.

A pesar de no resolver el problema de la materia oscura, se ha demostrado que la microlente es una herramienta útil para muchas aplicaciones. Cientos de eventos de microlente se detectan cada año hacia el centro galáctico, donde la profundidad óptica de microlente (debido a las estrellas en el disco galáctico) es aproximadamente 20 veces mayor que a través del halo galáctico. En 2007, el proyecto OGLE identificó 611 candidatos al evento, y el proyecto MOA (una colaboración entre Japón y Nueva Zelanda)[24] identificó 488 (aunque no todos los candidatos resultan ser eventos de microlente, y hay una superposición significativa entre los dos proyectos). Además de estas encuestas, se están llevando a cabo proyectos de seguimiento para estudiar en detalle eventos potencialmente interesantes en progreso, principalmente con el objetivo de detectar planetas extrasolares. Estos incluyen MiNDSTEp,[25] RoboNet, MicroFUN[26] y PLANET.[27]

En septiembre de 2020, los astrónomos que utilizan técnicas de microlente informaron de la detección, por primera vez, de un planeta errante de masa terrestre no limitado por ninguna estrella y que viaja libremente en la Vía Láctea.[28][29]

La microlente no sólo amplía la fuente, sino que también desplaza su posición aparente. Su duración es mayor que la del aumento, y puede utilizarse para encontrar la masa de la lente. En 2022 se informó de que esta técnica se utilizó para hacer la primera detección inequívoca de un agujero negro aislado de masa estelar, utilizando observaciones del telescopio espacial Hubble que se extendieron durante seis años, comenzando en agosto de 2011 poco después de que se detectara el evento de microlente. El agujero negro tiene una masa de unas 7 veces la masa solar y está a unos 1,6 kiloparsecs (5,2 mil años luz), en Sagitario, mientras que la estrella está a unos 6 kiloparsecs (20 mil años luz). Hay millones de agujeros negros aislados en nuestra galaxia, y al estar aislados se emite muy poca radiación desde su entorno, por lo que sólo pueden ser detectados por microlente. Los autores esperan que se encuentren muchos más con futuros instrumentos, concretamente el Telescopio espacial Nancy Grace Roman y el Observatorio Vera C. Rubin.[30]

Las matemáticas de la microlente, junto con la notación moderna, son descritas por Gould[31] y usamos su notación en esta sección, aunque otros autores han usado otra notación. El radio de Einstein, también llamado ángulo de Einstein, es el radio angular del anillo de Einstein en caso de alineación perfecta. Depende de la masa de la lente M, la distancia de la lente d_L y la distancia de la fuente d_S:

${\displaystyle \theta _{E}={\sqrt {{\frac {4GM}{c^{2}}}{\frac {d_{S}-d_{L}}{d_{S}d_{L}}}}}}$ (en radianes).

Para M igual a 60 masas de Júpiter, d_L = 4000 parsecs y dS = 8000 parsecs (típico de un evento de microlente de Bulge), el radio de Einstein es de 0,00024 segundos de arco[32] ángulo subtendido por 1 ua a 4000 parsecs).[33] En comparación, las observaciones terrestres ideales tienen una resolución angular de alrededor de 0,4 segundos de arco, 1660 veces mayor. Dado que ${\displaystyle \theta _{E}}$ es tan pequeño, generalmente no se observa para un evento de microlente típico, pero se puede observar en algunos eventos extremos como se describe a continuación.

Aunque no hay un comienzo o final claro de un evento de microlente, por convención se dice que el evento dura mientras que la separación angular entre la fuente y la lente es menor que ${\displaystyle \theta _{E}}$. Por tanto, la duración del evento está determinada por el tiempo que tarda el movimiento aparente de la lente en el cielo para cubrir una distancia angular ${\displaystyle \theta _{E}}$. El radio de Einstein también es del mismo orden de magnitud que la separación angular entre las dos imágenes con lente y el cambio astrométrico de las posiciones de la imagen a lo largo del curso del evento de microlente.

Durante un evento de microlente, el brillo de la fuente se amplifica mediante un factor de amplificación A. Este factor depende únicamente de la proximidad de la alineación entre el observador, la lente y la fuente. El número sin unidad u se define como la separación angular de la lente y la fuente, dividida por 5. El factor de amplificación se da en términos de este valor:[34]

${\displaystyle A(u)={\frac {u^{2}+2}{u{\sqrt {u^{2}+4}}}}.}$

Esta función tiene varias propiedades importantes. A(u) siempre es mayor que 1, por lo que la microlente solo puede aumentar el brillo de la estrella fuente, no disminuirlo. A(u) siempre disminuye a medida que aumenta u, por lo que cuanto más cerca está la alineación, más brillante se vuelve la fuente. Cuando u se acerca al infinito, A(u) se acerca a 1, de modo que en separaciones amplias, la microlente no tiene ningún efecto. Finalmente, cuando u se acerca a 0, para una fuente puntual A(u) se acerca al infinito cuando las imágenes se acercan a un anillo de Einstein. Para una alineación perfecta (u = 0), A(u) es teóricamente infinito. En la práctica, los objetos del mundo real no son fuentes puntuales, y los efectos de tamaño de fuente finito establecerán un límite a la amplificación que puede producirse para una alineación muy cercana,[35] pero algunos eventos de microlentes pueden causar un brillo por un factor de cientos.

A diferencia de la macrolente gravitacional donde la lente es una galaxia o cúmulo de galaxias, en la microlente u cambia significativamente en un corto período de tiempo. La escala de tiempo relevante se llama tiempo de Einstein, y viene dada por el tiempo que tarda la lente en recorrer una distancia angular ${\displaystyle \theta _{E}}$ en relación con la fuente en el cielo. Para eventos típicos de microlente, ${\displaystyle t_{E}}$ es del orden de unos pocos días a unos meses. La función u(t) simplemente está determinada por el teorema de Pitágoras:

${\displaystyle u(t)={\sqrt {u_{min}^{2}+\left({\frac {t-t_{0}}{t_{E}}}\right)^{2}}}.}$

El valor mínimo de u, llamado u_min, determina el brillo máximo del evento.

En un evento típico de microlente, la curva de luz se ajusta bien asumiendo que la fuente es un punto, la lente es una masa de un solo punto y la lente se mueve en línea recta: la aproximación de la lente del punto fuente-punto. En estos eventos, el único parámetro físicamente significativo que se puede medir es la escala de tiempo de Einstein ${\displaystyle t_{E}}$. Dado que este observable es una función degenerada de la masa, la distancia y la velocidad de la lente, no podemos determinar estos parámetros físicos a partir de un solo evento.

Sin embargo, en algunos eventos extremos, ${\displaystyle \theta _{E}}$ puede ser medible, mientras que otros eventos extremos pueden probar un parámetro adicional: el tamaño del anillo de Einstein en el plano del observador, conocido como el radio de Einstein proyectado: ${\displaystyle {\tilde {r}}_{E}}$. Este parámetro describe cómo aparecerá el evento. ser diferente de dos observadores en diferentes ubicaciones, como un observador satelital. El radio de Einstein proyectado está relacionado con los parámetros físicos de la lente y la fuente por

${\displaystyle {\tilde {r}}_{E}={\sqrt {{\frac {4GM}{c^{2}}}{\frac {d_{S}d_{L}}{d_{S}-d_{L}}}}}.}$

Es matemáticamente conveniente utilizar las inversas de algunas de estas cantidades. Estos son el movimiento propio de Einstein

${\displaystyle {\vec {\mu }}_{E}={t_{E}}^{-1}}$

Y el paralaje de Einstein

${\displaystyle {\vec {\pi }}_{E}={{\tilde {r}}_{E}}^{-1}.}$

Estas cantidades vectoriales apuntan en la dirección del movimiento relativo de la lente con respecto a la fuente. Algunos eventos extremos de microlentes solo pueden restringir un componente de estas cantidades vectoriales. Si estos parámetros adicionales se miden por completo, los parámetros físicos de la lente se pueden resolver produciendo la masa de la lente, el paralaje y el movimiento adecuado como:

${\displaystyle M={\frac {c^{2}}{4G}}\theta _{E}{\tilde {r}}_{E},}$

${\displaystyle \pi _{L}=\pi _{E}\theta _{E}+\pi _{S},}$

${\displaystyle \mu _{L}=\mu _{E}\theta _{E}+\mu _{S}.}$

En un evento de microlente típico, la curva de luz se ajusta bien al asumir que la fuente es un punto, la lente es una masa de un solo punto y la lente se mueve en línea recta: la aproximación de la lente puntual de punto de origen. En estos eventos, el único parámetro físicamente significativo que se puede medir es la escala de tiempo de Einstein ${\displaystyle t_{E}}$. Sin embargo, en algunos casos, los eventos pueden analizarse para obtener los parámetros adicionales del ángulo y del paralaje de Einstein: ${\displaystyle \theta _{E}}$ y ${\displaystyle \pi _{E}}$. Estos incluyen eventos de gran aumento, lentes binarios, paralaje y eventos xallarap, y eventos donde la lente es visible.

Microlente gravitacional de un planeta extrasolar.

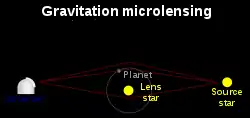
Si el objeto de lente es una estrella con un planeta en órbita, este es un ejemplo extremo de un evento de lente binario. Si la fuente cruza un cáustico, las desviaciones de un evento estándar pueden ser grandes incluso para planetas de baja masa. Estas desviaciones nos permiten inferir la existencia y determinar la masa y la separación del planeta alrededor de la lente. Las desviaciones suelen durar unas pocas horas o unos pocos días. Debido a que la señal es más fuerte cuando el evento en sí es más fuerte, los eventos de gran aumento son los candidatos más prometedores para un estudio detallado. Típicamente, un equipo de encuesta notifica a la comunidad cuando descubren un evento de gran aumento en progreso. Los grupos de seguimiento luego monitorean intensamente el evento en curso, con la esperanza de obtener una buena cobertura de la desviación si ocurre. Cuando termina el evento, la curva de luz se compara con los modelos teóricos para encontrar los parámetros físicos del sistema. Los parámetros que se pueden determinar directamente a partir de esta comparación son la relación de masa del planeta a la estrella y la relación de la separación angular estrella-planeta al ángulo de Einstein. A partir de estas relaciones, junto con las suposiciones sobre la estrella del lente, se puede estimar la masa del planeta y su distancia orbital.

Se descubrieron exoplanetas usando microlentes, por año, hasta 2014.

Comparando este método de detección de planetas extrasolares con otras técnicas como el método de tránsito, una ventaja es que la intensidad de la desviación planetaria no depende de la masa planetaria tan fuertemente como lo hacen los efectos en otras técnicas. Esto hace que la microlente sea adecuada para encontrar planetas de baja masa. También permite la detección de planetas más alejados de la estrella anfitriona que la mayoría de los otros métodos. Una desventaja es que el seguimiento del sistema de lentes es muy difícil después de que el evento ha finalizado, ya que toma mucho tiempo para que la lente y la fuente se separen suficientemente para resolverlas por separado.

Hay dos tipos básicos de experimentos de microlentes. Los grupos de "búsqueda" usan imágenes de gran campo para encontrar nuevos eventos de microlente. Los grupos de "seguimiento" a menudo coordinan telescopios en todo el mundo para proporcionar una cobertura intensiva de eventos seleccionados. Todos los experimentos iniciales tenían nombres algo atrevidos hasta la formación del grupo PLANET. Existen propuestas actuales para construir nuevos satélites microlentes especializados o para usar otros satélites para estudiar la microlente.

• Descubrimiento de un planeta cinco veces más masivo que la tierra que orbita una estrella a 20,000 años luz de distancia