Miriágono
En geometría, un miriágono o 10000-gono es un polígono con 10.000 lados. Varios filósofos han utilizado el miriágono regular para ilustrar cuestiones relativas al pensamiento.[1][2][3][4][5]
| Miriágono | ||
|---|---|---|
 Un miriágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 10.000 | |
| Vértices | 10 000 | |
| Grupo de simetría | Diedral (D10000), orden 2×10000 | |
| Símbolo de Schläfli | {10000}, t{5000}, tt{2500}, ttt{1250}, tttt{625} (miriágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
| Ángulo interior | 179,964° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Miriágono regular
Un miriágono regular está representado por el símbolo de Schläfli {10.000} y se puede construir como un truncamiento de un 5000-gono o t {5000}; como un truncamiento doble de un 2500-gono o tt {2500}; como un truncamiento triple de un 1250-gono o ttt{1250); o como un truncamiento cuádruple de un 625-gono o tttt {625}.
La medida de cada ángulo interno en un miriágono regular es de 179,964°. El área de un miriágono regular con lados de longitud a viene dado por:
El resultado difiere del área de su circunferencia circunscrita en tan solo 40 partes entre mil millones.
Dado que 10.000 = 24×54, el número de lados no es un producto de números de Fermat distintos ni una potencia de dos. Por lo tanto, el miriágono regular no es un polígono construible. De hecho, ni siquiera se puede construir con el uso del método neusis o mediante un trisector de ángulo, ya que el número de lados no es un producto de números primos de Pierpont distintos, ni un producto de potencias de dos y tres.
Simetría
El "miriágono regular" posee la simetría diedral Dih10000, orden 20000, representada por 10000 ejes de reflexión. Dih100 tiene 24 subgrupos diedrales: (Dih5000, Dih2500, Dih1250, Dih625), (Dih2000, Dih1000, Dih500, Dih250, Dih125), (Dih400, Dih200, Dih100, Dih50, Dih25), (Dih80, Dih40, Dih20, Dih10, Dih5) y (Dih16, Dih8, Dih4, Dih2, Dih1).
También posee 25 simetrías cíclicas más como subgrupos: (Z10000, Z5000, Z2500, Z1250, Z625), (Z2000, Z1000, Z500, Z250, Z125), (Z400, Z200, Z100, Z50, Z25), (Z80, Z40, Z20, Z10), y (Z16, Z8, Z4, Z2, Z1), con Zn representando la simetría rotacional de π/n radianes.
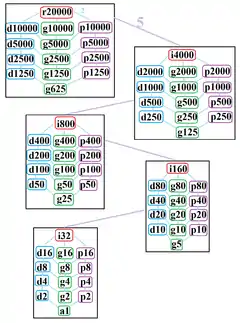
John Conway etiqueta estas simetrías inferiores con una letra y con el orden de la simetría detrás de la letra.[6] r20000 representa simetría completa y a1 denota la ausencia de simetría. La letra d (diagonal) indica ejes de simetría a través de vértices, p ejes de simetría a través de lados (perpendiculares), i ejes de simetría a través de vértices y lados, y la letra g indica una simetría rotacional.
Estas simetrías más bajas permiten grados de libertad para definir miriágonos irregulares. Solo el subgrupo g10000 no tiene grados de libertad, y puede verse como un grafo dirigido.
Miriagrama
Un miriagrama es una estrella de 10.000 lados. Hay 1999 formas regulares[7] dadas por símbolos de Schläfli de la forma {10000/n}, donde n es un número entero entre 2 y 5000, que es coprimo respecto a 10.000. También hay 3000 formas de estrellas regulares en los casos restantes.
En la cultura popular
- En la novela Flatland, romance of many dimensions, se supone que el Círculo Jefe tiene diez mil lados, lo que lo convierte en un miríadago.
Véase también
Referencias
- Meditation VI by Descartes (English translation).
- Hippolyte Taine, On Intelligence: pp. 9–10
- Jacques Maritain, An Introduction to Philosophy: p. 108
- Alan Nelson (ed.), A Companion to Rationalism: p. 285
- Paolo Fabiani, The philosophy of the imagination in Vico and Malebranche: p. 222
- The Symmetries of Things, Chapter 20
- 5000 casos - 1 (convexo) - 1000 (múltiplos de 5) - 2500 (múltiplos de 2) + 500 (múltiplos de 2 y de 5)