Núcleo (matemática)
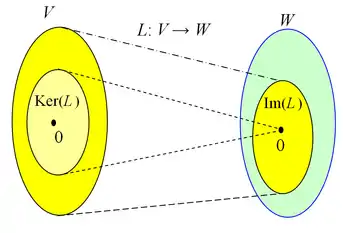
En matemáticas y especialmente en álgebra lineal, dada la transformación lineal , el kernel o núcleo de , denotado por o , se define como el conjunto de todos los vectores en cuya imagen bajo sea el vector nulo de , es decir, el se define como
Ejemplos
Considere la función
que es lineal cumple que para y
- .
Su núcleo consiste en todos aquellos vectores cuya primera y segunda coordenada coinciden pues
en concreto el es el conjunto:
que es el mismo que la variedad lineal generada por el vector (1,1), que describe la recta en .
En el espacio euclídeo de dimensión 3, el núcleo de una forma lineal está formado por todos aquellos vectores que son ortogonales a uno dado. Por ejemplo, dado el vector a = (1,2,3), la forma lineal dada por el producto escalar tiene por núcleo los vectores que satisfacen la ecuación matricial
- ,
que equivale a la ecuación lineal:
- .
La solución es otro subespacio de dimensión 2, que se puede describir por ejemplo como el subespacio generado por los vectores: .
Propiedades
Dado un operador lineal con matriz asociada , el núcleo es un subespacio de , cuya dimensión se denomina nulidad de , que coincide con el número de columnas que no tienen pivotes al reducir por filas la matriz . El teorema rango-nulidad establece que el rango más la nulidad es igual al número de columnas de la matriz.
Véase también
Enlaces externos
- Weisstein, Eric W. «Kernel». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Kernel of a linear mapping en PlanetMath.