Número primo de Mersenne

Demostración
Si n es un número natural, por el teorema del binomio se tiene:

${\displaystyle c^{n}-d^{n}=(c-d)\sum _{k=0}^{n-1}c^{k}d^{n-1-k}}$,

Tomando ${\displaystyle c=2}$, ${\displaystyle d=1}$ y ${\displaystyle n=ab}$ (a, b > 1), se tiene:

${\displaystyle M_{n}=M_{ab}=2^{ab}-1=(2^{a})^{b}-1^{b}=(2^{a}-1)\sum _{k=0}^{b-1}(2^{a})^{k}1^{b-1-k}=(2^{a}-1)\cdot \left(1+2^{a}+2^{2a}+2^{3a}+\dots +2^{(b-1)a}\right)}$

${\displaystyle 2^{a}-1}$ es mayor que 1 porque se ha procurado que ${\displaystyle a}$ sea estrictamente mayor que 1, y la suma ${\displaystyle 1+2^{a}+2^{2a}+2^{3a}+\dots +2^{(b-1)a}}$ también lo es. Por tanto, se tiene una factorización de ${\displaystyle M_{n}}$, así que ${\displaystyle M_{n}}$ es compuesto.

Observación: Por contraposición, si M_n es primo, entonces n es primo. Esto facilita la búsqueda de nuevos números primos de Mersenne M_n, ya que solo hay que comprobar la primalidad de aquellos para los que n es primo.

• Ejemplo I: ${\displaystyle 2^{5}-1=31}$ es primo, siendo:

31 = 6 · 5 + 1

• Ejemplo II: ${\displaystyle 2^{11}-1=2047=23\cdot 89}$, siendo:

23 = 2 · 11 + 1

89 = 8 · 11 + 1

2047 = 186 · 11 + 1

Demostración

Si q es un primo que divide ${\displaystyle 2^{p}-1}$, entonces ${\displaystyle 2^{p}}$ ≡ 1 (mod q). Por el Pequeño Teorema de Fermat, ${\displaystyle 2^{q-1}}$ ≡ 1 (mod q). Supongamos que p que no divide a q − 1 para llegar a contradicción. Entonces, como p y q − 1 deben ser primos entre sí, una nueva aplicación del Pequeño Teorema de Fermat muestra que ${\displaystyle (q-1)^{p-1}}$ ≡ 1 (mod p). Por tanto, existe un número x ≡ ${\displaystyle (q-1)^{p-2}}$ tal que (q − 1)·x ≡ 1 (mod p), y por tanto un número k tal que (q − 1)·x − 1 = kp.

Como ${\displaystyle 2^{q-1}}$ ≡ 1 (mod q), al elevar ambos lados de la congruencia a la potencia x resulta ${\displaystyle 2^{(q-1)x}}$ ≡ 1, y como ${\displaystyle 2^{p}}$ ≡ 1 (mod q), al elevar ambos lados de esta segunda congruencia a la potencia k resulta ${\displaystyle 2^{pk}}$ ≡ 1. Por tanto, 1≡ ${\displaystyle {\frac {2^{(q-1)x}}{2^{pk}}}}$ ≡ ${\displaystyle 2^{(q-1)x-pk}}$ (mod q). Pero teníamos que (q − 1)x − kp = 1, lo que implica que ${\displaystyle 2^{1}}$ ≡ 1 (mod q); en otras palabras, que q divide 1. Con esto, la premisa inicial de que p no divide q − 1 es insostenible.

Por lo tanto, ${\displaystyle q=n\cdot p+1}$. Pero, además, este n tiene que ser par, porque ${\displaystyle 2^{p}-1}$ es impar y todos sus divisores deben ser también impares. Como p era un primo impar, la única manera que esto ocurra es que ${\displaystyle n=2k}$ y, finalmente, ${\displaystyle q=2kp+1}$.

Demostración

${\displaystyle 2^{p+1}=2{\pmod {q}}}$, así que ${\displaystyle 2^{(p+1)/2}}$ es una raíz cuadrada de 2 módulo ${\displaystyle q}$.
Por reciprocidad cuadrática, cualquier módulo primo del cual 2 tenga raíz cuadrada es congruente con ${\displaystyle \pm 1{\pmod {8}}}$.

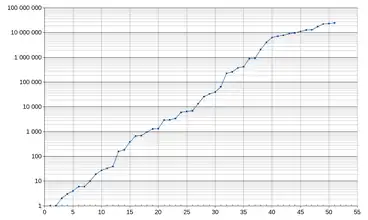Gráfico que representa el número de cifras de cada uno de los primos de Mersenne conocidos. Nótese que la escala vertical es logarítmica.

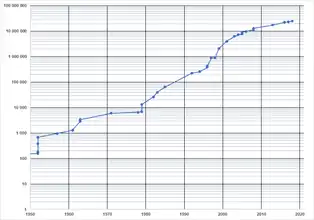Gráfico del número de cifras del primo de Mersenne más grande que se conocía cada año (era electrónica). La escala vertical es logarítmica.

La siguiente tabla muestra los números primos de Mersenne conocidos:

No se conoce si existen más números primos de Mersenne entre el 48.º (M_43.112.609) y el 51.º (M_82.589.933). Por lo tanto, esta tabla es provisional. Por poner un ejemplo histórico, el 29.º número primo de Mersenne fue descubierto después del 30.º y el 31.º.

Desmentida la conjetura original de Mersenne (que establecía una lista de números primos de Mersenne menores o iguales que M₂₅₇ y afirmaba que no existían más que esos), han surgido otras preguntas abiertas relacionadas con la caracterización de estos números. En particular, la conjetura de Bateman, Selfridge y Wagstaff (1989) también recibe el nombre de "Nueva conjetura de Mersenne".

• Constante de Erdős–Borwein
• Número perfecto
• Número primo de Fermat
• Número primo de Wagstaff
• Número primo de Wieferich
• Repunit
• Test de Lucas-Lehmer

• Sección dedicada a los números primos de Mersenne en The Prime Pages, en inglés
• GIMPS: proyecto distribuido de búsqueda de números primos de Mersenne, en inglés.
• Determinación geométrica de los números primos y perfectos